Complex analysis on 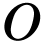 -minimal
structures -minimal
structures |
|
| February–March 2022 |
|
Definition 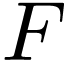 together with a topology
together with a topology  on
on 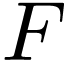 for which the sum,
product, additive and multiplicative inverse functions are
continuous.
for which the sum,
product, additive and multiplicative inverse functions are
continuous.
The space 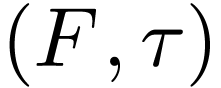 is Hausdorff.
is Hausdorff.
If 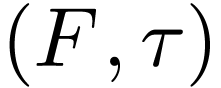 is compact, then
is compact, then 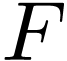 is finite.
is finite.
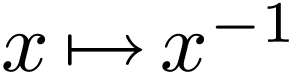 has no limit at
has no limit at  .
.
There exists a non-empty open proper subset of 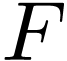 .
.
Example
Finite fields with the discrete topology.
Linearly ordered fields with the order topology.
If 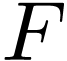 is any field, then the field
is any field, then the field 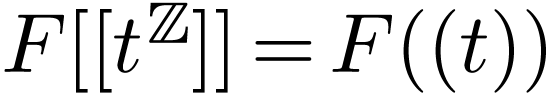 of formal Laurent series with the valuation topology
(in fact any valued field). Note that
of formal Laurent series with the valuation topology
(in fact any valued field). Note that 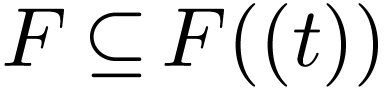 is
closed, and that the induced topology on
is
closed, and that the induced topology on 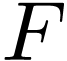 is
the discrete topology.
is
the discrete topology.
Let 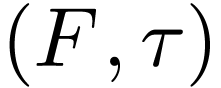 be a topological field, and consider an
algebraic extension
be a topological field, and consider an
algebraic extension 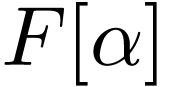 .
Then
.
Then 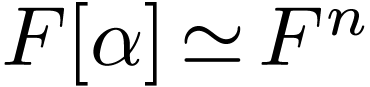 as a vector space over
as a vector space over 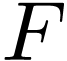 . The product topology then induces a
topological field.
. The product topology then induces a
topological field.
We fix a topological field 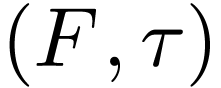 .
.
Definition 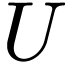 be open, let
be open, let 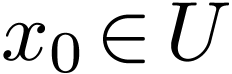 and let
and let 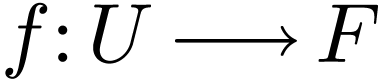 . Then
. Then 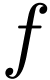 is said
differentiable if there exists a
is said
differentiable if there exists a 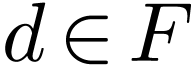 such that
such that
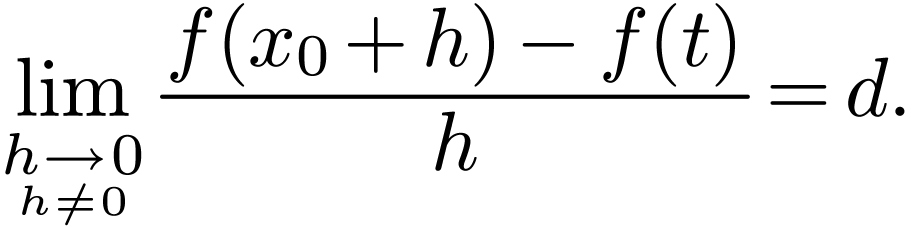
The number 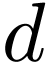 is unique, and we write
is unique, and we write 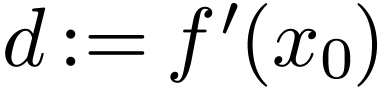 .
.
This is preserved by sums, products, quotients, composition and so on. Moreover differentiability implies continuity. We also have the Cauchy-Riemann equations.
We will next consider more specific contexts: 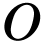 -minimality in particular.
-minimality in particular.
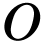 -minimal
case
-minimal
case
Let 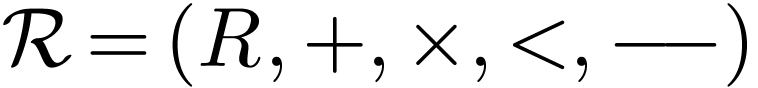 be
be 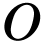 -minimal
and write
-minimal
and write 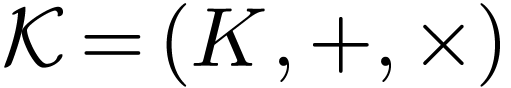 for its algebraic closure
for its algebraic closure 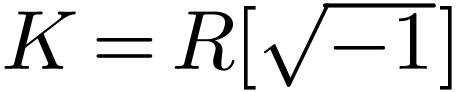 . Any
. Any 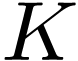 -rational
function is differentiable.
-rational
function is differentiable.
Consider the case of 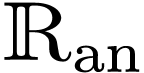 . If
. If
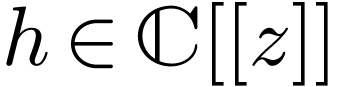 converges in a neighborhood of zome
converges in a neighborhood of zome 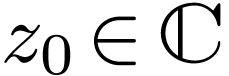 , then there is some open
, then there is some open 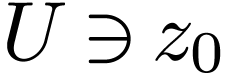 such that
such that 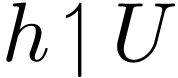 is definable in
is definable in 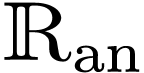 .
.
On  , the function
, the function 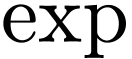 is not definable in any
is not definable in any 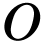 -minimal
expansion of
-minimal
expansion of 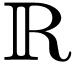 . Fact: let
. Fact: let 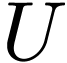 be open such that
be open such that 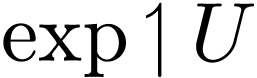 is
definable in some
is
definable in some 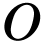 -minimal
expansion of
-minimal
expansion of 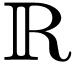 . Then the
imaginary part of
. Then the
imaginary part of 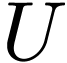 must be bounded. Indeed,
defining
must be bounded. Indeed,
defining 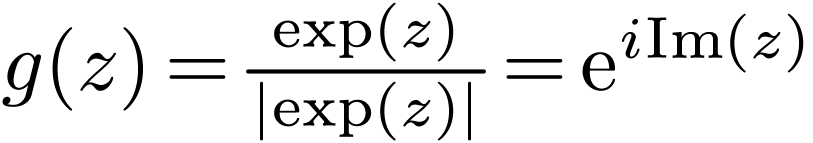 on
on 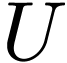 ,
and the set
,
and the set 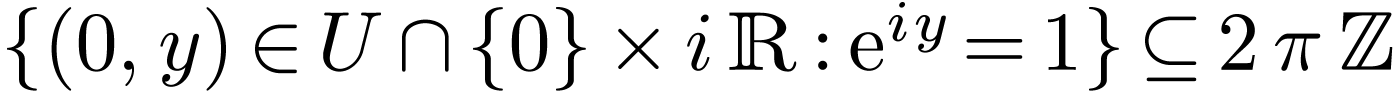 (project onto the
(project onto the 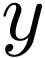 -axis if you must) must be bounded by
-axis if you must) must be bounded by  -minimality. Conversely, in
-minimality. Conversely, in 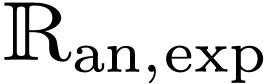 , each such
, each such 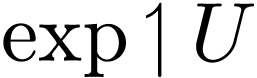 is definable whenever
is definable whenever 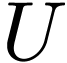 is definable. In
particular
is definable. In
particular 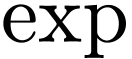 is defined and injective on the strip
of
is defined and injective on the strip
of 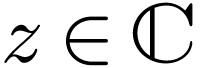 with
with 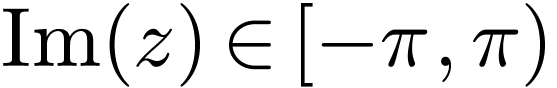 .
So
.
So 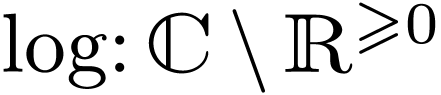 is definable.
is definable.
Question 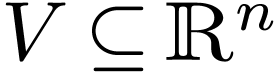 is open and
is open and 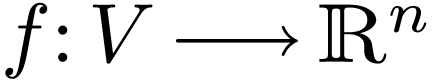 is real-analytic and
definable in some
is real-analytic and
definable in some  -minimal
expansion of
-minimal
expansion of  , then when can
, then when can
 be extended definably to some
be extended definably to some 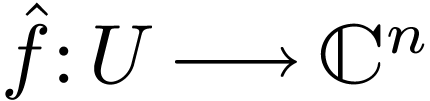 which is complex-analytic, where
which is complex-analytic, where 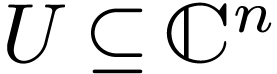 is open? This is open for
is open? This is open for 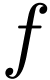 definable in
definable in
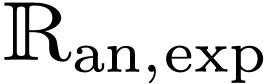 .
.
Answer 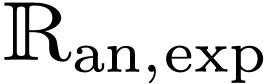 . Andre Opris shows in his PhD thesis that this is
the case for a large class of functions called restricted
. Andre Opris shows in his PhD thesis that this is
the case for a large class of functions called restricted 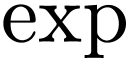 -
-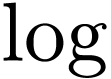 -analytic
functions, which is a proper subset of the set of definable functions in
-analytic
functions, which is a proper subset of the set of definable functions in
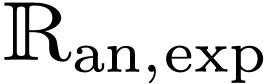 .
.
Consider the field 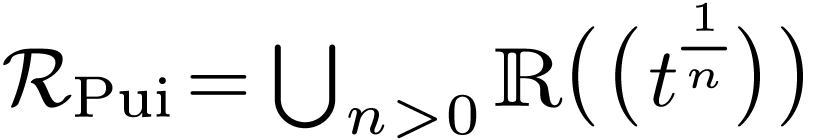 of formal Puiseux series over
of formal Puiseux series over
 , where
, where  is a positive infinitesimal. The field
is a positive infinitesimal. The field 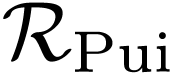 is
real-closed. Let
is
real-closed. Let 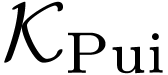 denote its algebraic closure.
For all
denote its algebraic closure.
For all 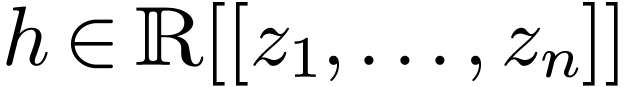 (formal power series), we have a
function
(formal power series), we have a
function 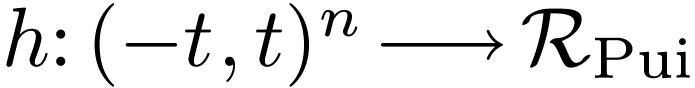 . Write
. Write  for the structure
for the structure 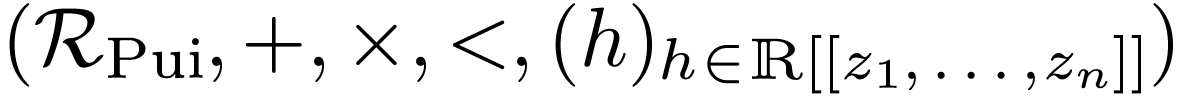 .
Robinson and Lipshitz showed that this is
.
Robinson and Lipshitz showed that this is  -minimal.
Any such function
-minimal.
Any such function 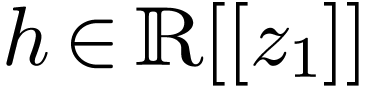 can be dedinably extended to
can be dedinably extended to
 .
.
We fix an 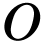 -minimal expansion
-minimal expansion
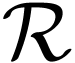 of a real-closed field
of a real-closed field 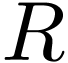 , and write
, and write 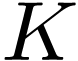 for the
algebraic closure of
for the
algebraic closure of 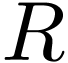 .
.
Everything will be definable.
Definition 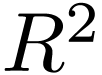 is a definable and continuous
is a definable and continuous 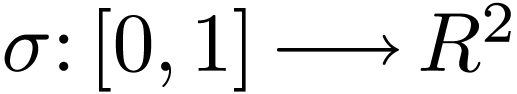 with
with
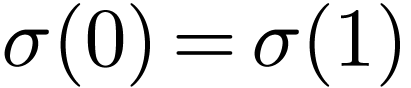 . We sometimes write
. We sometimes write 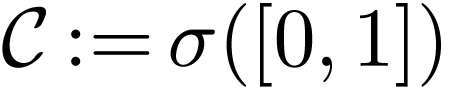 . The curve
. The curve  is called simple if
is called simple if 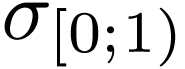 is injective.
is injective.
Example 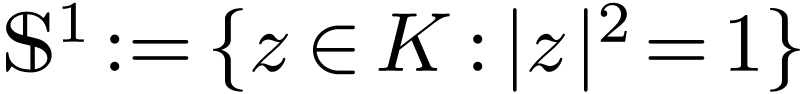 . We fix some simple counter-clockwise
semi-algebraic parametrization
. We fix some simple counter-clockwise
semi-algebraic parametrization  of
of 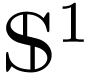 .
.
Given any closed curve 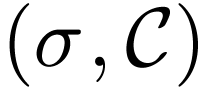 and a definable
continuous map
and a definable
continuous map 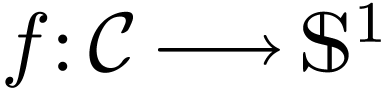 . We have maps
. We have maps
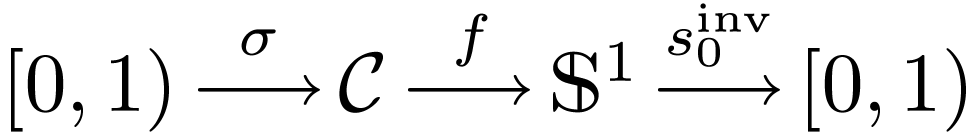
choosing 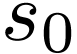 so that
so that 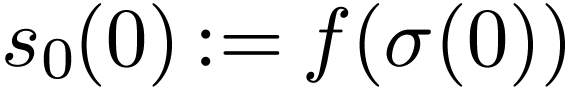 .
Write
.
Write 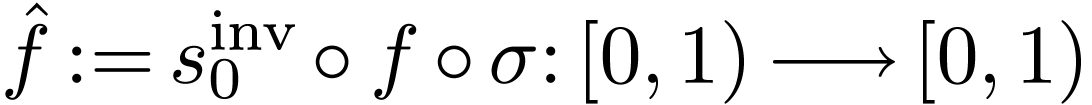 . For simplicity,
assume that
. For simplicity,
assume that 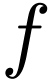 is not locally constant anywhere.
The only possible discontinuities lie in
is not locally constant anywhere.
The only possible discontinuities lie in 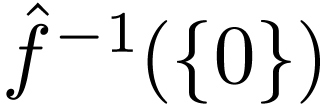 ,
which by
,
which by 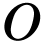 -minimality, is
finite. Write
-minimality, is
finite. Write 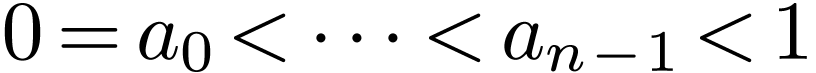 be the discontinuities. We add
be the discontinuities. We add
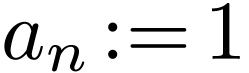 as a point, in order to define the winding
number of
as a point, in order to define the winding
number of 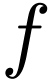 as follows. For
as follows. For 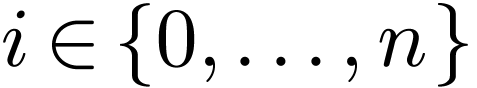 , write
, write
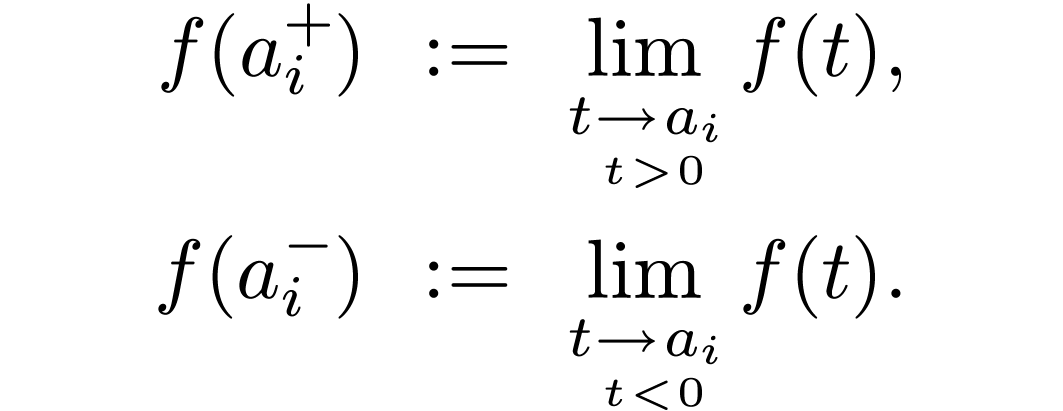
We define the winding number 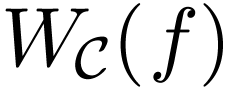 of
of 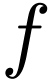 as
as
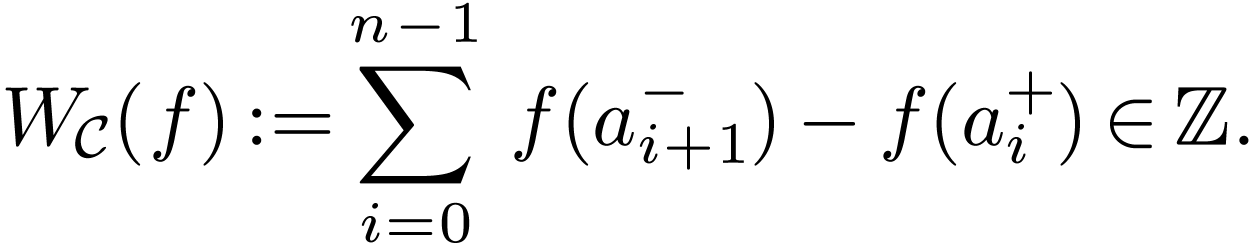
xample
Example 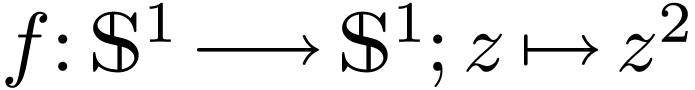 . Then
. Then 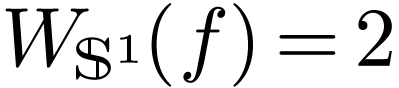 .
Also
.
Also 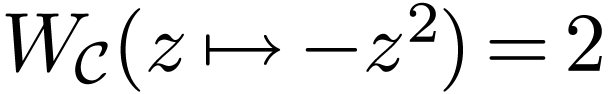 , and
, and 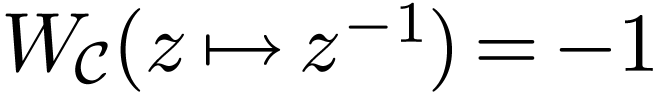 .
.
Remark 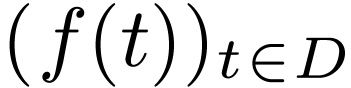 is a definable family of continuous functions
is a definable family of continuous functions 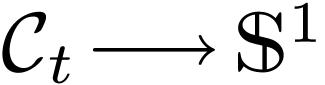 . Then by
. Then by 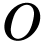 -minimality
the numbers
-minimality
the numbers 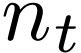 corresponding to
corresponding to 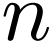 above are bounded, so the definition of
above are bounded, so the definition of 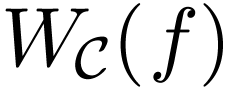 can be
done uniformly.
can be
done uniformly.
Let us give a few properties of those winding numbers.
If 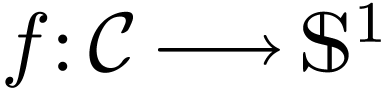 is not surjective, then
is not surjective, then 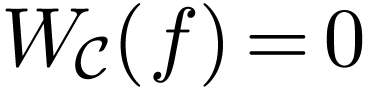 .
.
Let 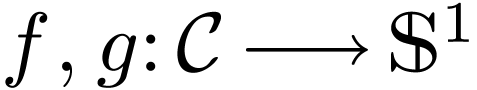 be definably holomorphic. Assume that
be definably holomorphic. Assume that
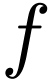 and
and 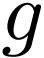 are
homotopy-equivalent, i.e. there is a continuous
are
homotopy-equivalent, i.e. there is a continuous 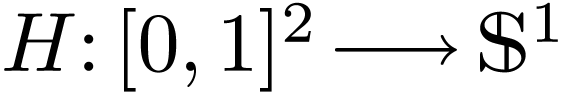 with
with 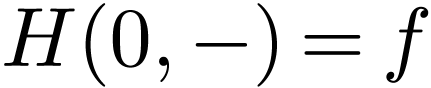 and
and 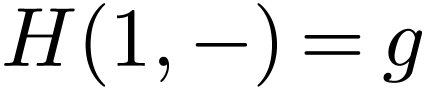 .
Then
.
Then 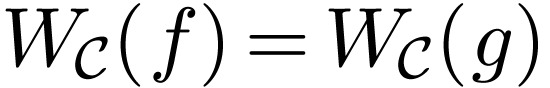 . This relies on the
facts that
. This relies on the
facts that 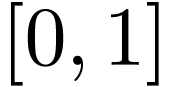 is dedinably connected in
is dedinably connected in 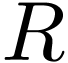 , and that the function
, and that the function 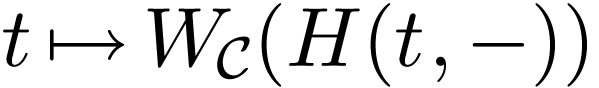 is locally constant.
is locally constant.
For continuous definable 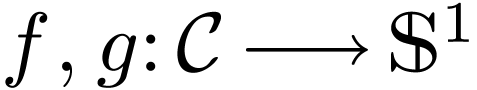 ,
we have
,
we have 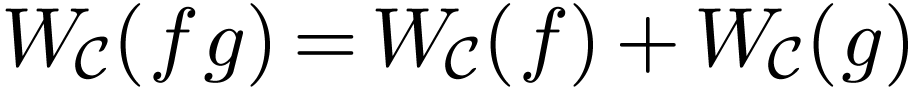 .
.
If one reverses the parametrization of 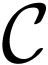 ,
then
,
then 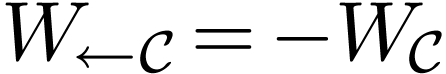 .
.
Definition 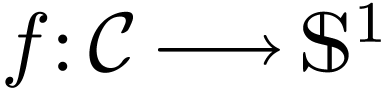 be definable and continuous, and let
be definable and continuous, and let 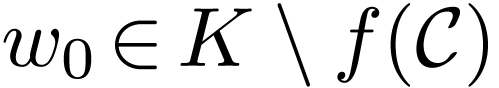 . We want to define the winding
number
. We want to define the winding
number 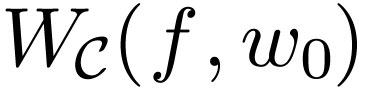 of
of 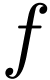 around
around 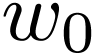 . We define
. We define 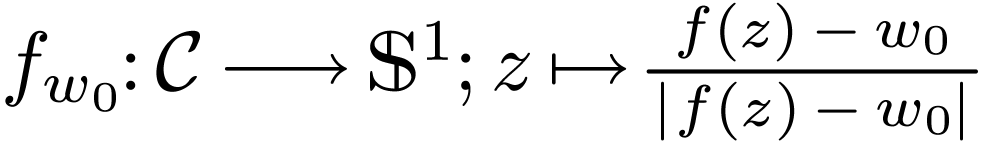 ,
and set
,
and set 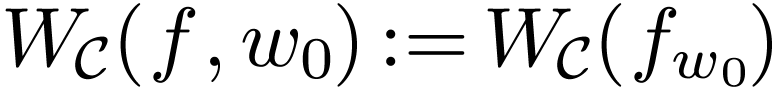 .
.
 -differentiability
-differentiability
Lemma 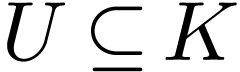 be definable, open and non-empty. Let
be definable, open and non-empty. Let 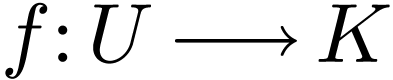 be definable and continuous, and let
be definable and continuous, and let 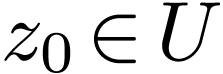 such that
such that
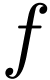 is
is  -differentiable
at
-differentiable
at  . If
. If 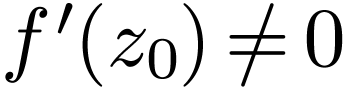 , then for all sufficiently small circles
, then for all sufficiently small circles 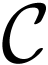 centered at
centered at  ,
we have
,
we have 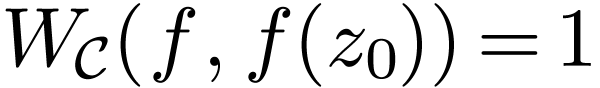 .
.
Proof. Write 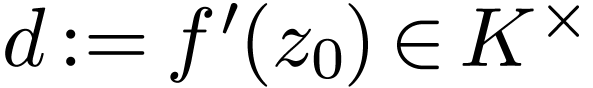 .
Since
.
Since 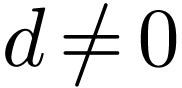 , there is a
, there is a 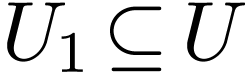 with
with 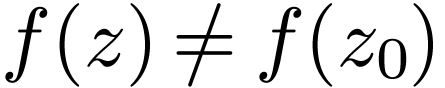 for all
for all 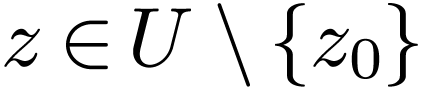 . So we can consider
. So we can consider 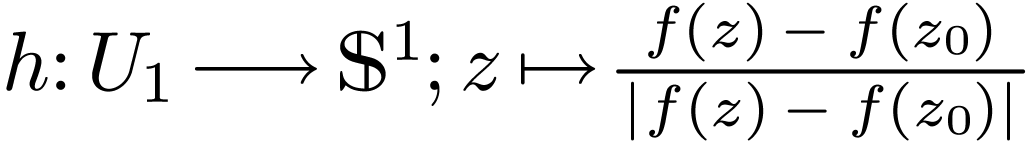 . Also set
. Also set
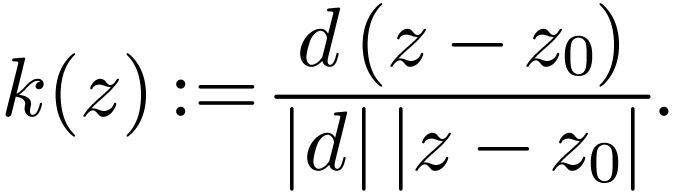
Note that  for all circles
for all circles  around
around  . Since
. Since 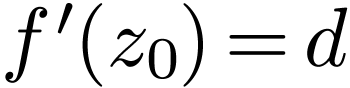 , for
, for 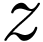 sufficiently
close to
sufficiently
close to  , the element
, the element 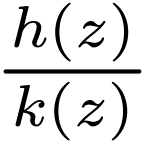 is close to
is close to  .
In particular, picking a sufficiently small circle
.
In particular, picking a sufficiently small circle  around
around  , the function
, the function 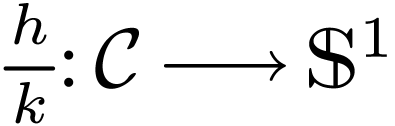 is not surjective. So
is not surjective. So 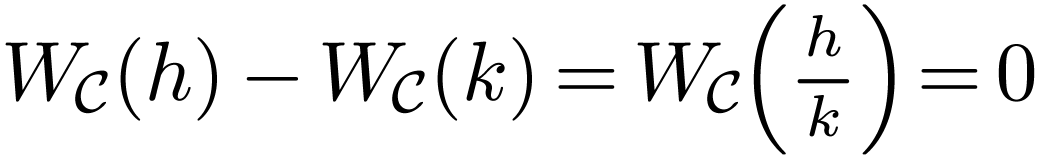 .
We conclude that
.
We conclude that 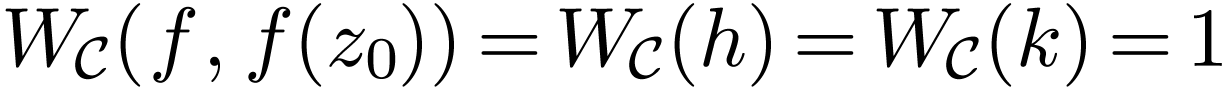 .
.
Write 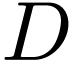 for the closed unit disk in
for the closed unit disk in 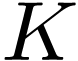 , and
, and 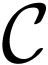 for the unit
circle, parametrized counter-clockwise.
for the unit
circle, parametrized counter-clockwise.
Main Lemma. Let 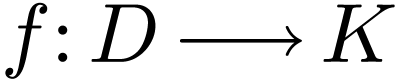 be definable and
be definable and  -differentiable
on
-differentiable
on 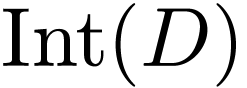 . Let
. Let 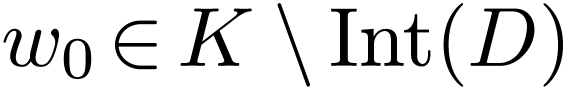 . We have
. We have
Example  -differentiable
-differentiable 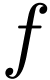 .
Let
.
Let 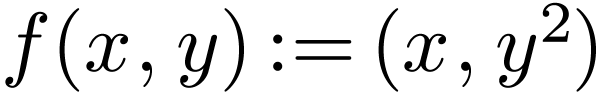 . So
. So 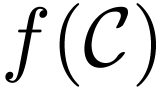 is an upper arc in
is an upper arc in  , and
, and 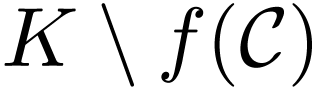 has one definably connected component, and has
winding number
has one definably connected component, and has
winding number 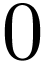 around any element in the
around any element in the 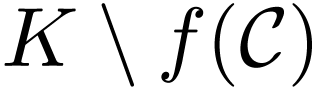 including those which lie in
including those which lie in 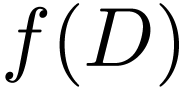 .
.
Proof of the Main Lemma. We first prove i. We can use
an homotopy to shrink 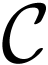 continuously, and as the
radius of
continuously, and as the
radius of 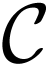 tends to
tends to 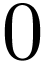 ,
the curve
,
the curve 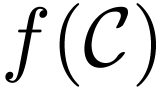 is close to
is close to 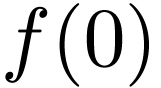 , so
, so 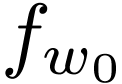 will not be surjective
(it will only cover a small angle). So the winding number of
will not be surjective
(it will only cover a small angle). So the winding number of 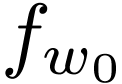 is
is 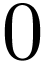 , hence the
result.
, hence the
result.
Let us now prove ii. Fix a definably connected and open component 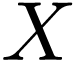 of
of 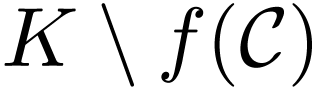 which contains
which contains 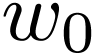 . Since
. Since 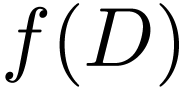 is
definably connected (because
is
definably connected (because 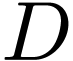 is and
is and 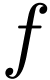 is continuous and definable), the point
is continuous and definable), the point 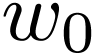 is not isolated in
is not isolated in 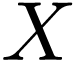 , so
, so 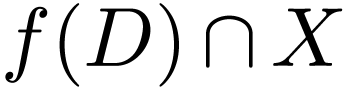 is infinite. Consider the open set
is infinite. Consider the open set 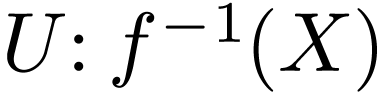 . We claim that the set
. We claim that the set
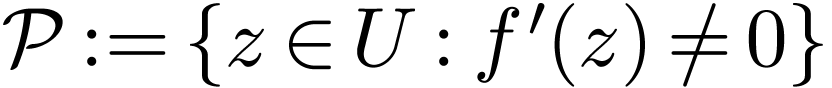
has dimention 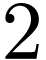 . Indeed assume
for contradiction that
. Indeed assume
for contradiction that  has dimension
has dimension 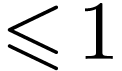 . Then in particular
. Then in particular 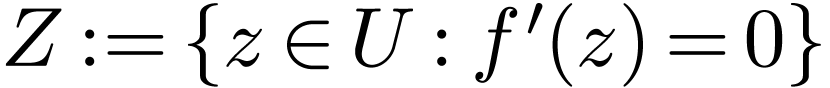 has codimension
has codimension 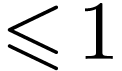 .
But
.
But 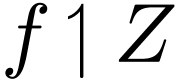 has differential
has differential 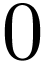 everywhere, so partitioning
everywhere, so partitioning  ,
we see that
,
we see that 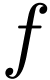 is locally constant, so takes only
finitely many values. So
is locally constant, so takes only
finitely many values. So 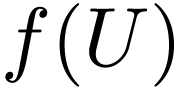 is finite:
contradicting the previous argument.
is finite:
contradicting the previous argument.
The statements of the main lemma are first-order, so we can move to a
sufficiently saturated elementary extension, and consider a generic
point  in
in 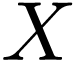 over
over  . Then
. Then 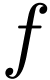 is
is
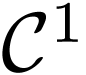 at
at  as an
as an 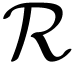 -function. Moreover
-function. Moreover 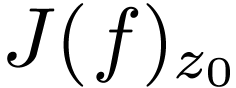 is
invertible (i.e.
is
invertible (i.e. 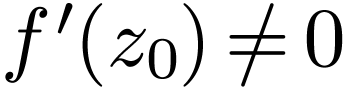 ), then the
inverse function theorem for
), then the
inverse function theorem for 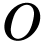 -minimal
structures gives that
-minimal
structures gives that 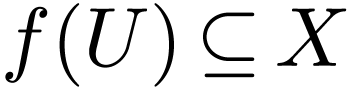 contains an open set,
whence in particular
contains an open set,
whence in particular 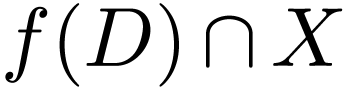 contains an open set.
contains an open set.
Pick 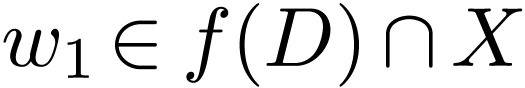 be generic, so
be generic, so 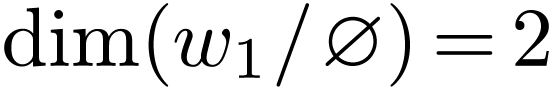 . We claim that
. We claim that 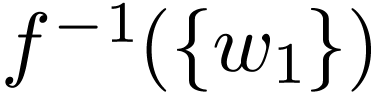 is finite
and that
is finite
and that 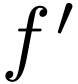 is non-zero on this set. Assume for
contradiction that
is non-zero on this set. Assume for
contradiction that 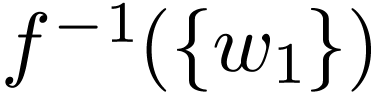 is infinite. Let
is infinite. Let 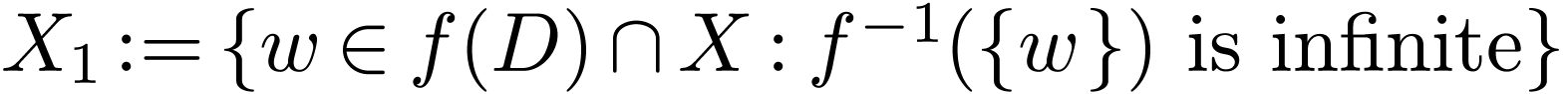 . Then
. Then 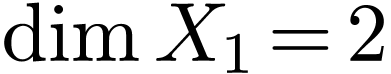 since it
contains the generic point
since it
contains the generic point 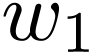 .
So
.
So 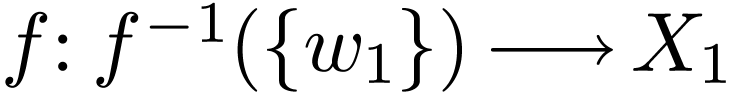 is surjectve for all such infinite fibers,
which is impossible since the dimentin of
is surjectve for all such infinite fibers,
which is impossible since the dimentin of 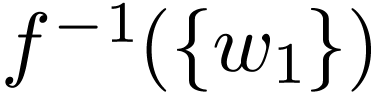 is
is
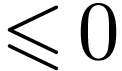 . Assume for contradiction
that there is
. Assume for contradiction
that there is 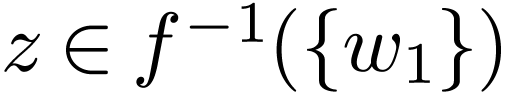 with
with 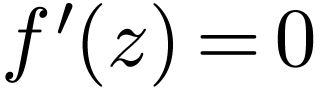 ,
and write
,
and write  for the set of such
for the set of such  's. Then again
's. Then again 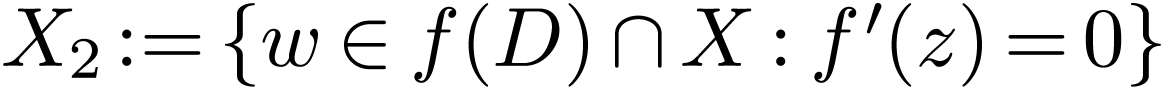 has
dimension
has
dimension 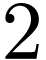 . By definable
choice, there is a
. By definable
choice, there is a  such that for all
such that for all  , there is a
, there is a 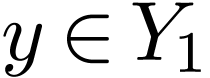 with
with 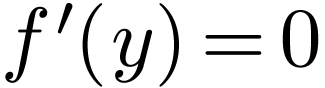 and this yields a similar
contradiction.
and this yields a similar
contradiction.
03-02: Lecture 5
Removal of singularities à la Riemann.
Let 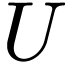 be open and non-empty, let
be open and non-empty, let 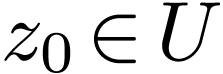 and let
and let 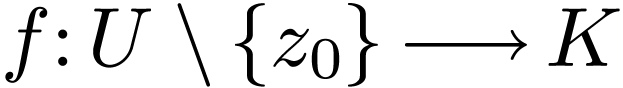 be definable,
be definable,  -differentiable and bounded. Then
there is a unique
-differentiable and bounded. Then
there is a unique 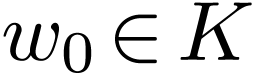 such that the extension of
such that the extension of
 to
to  with
with 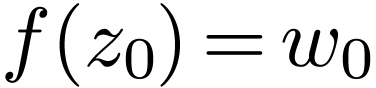 is
is  -differentiable.
-differentiable.
Proof. Set 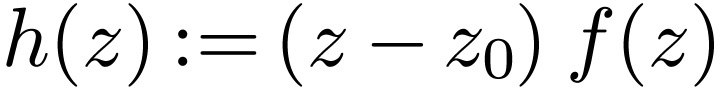 for
for 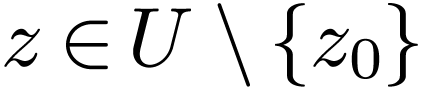 and
and 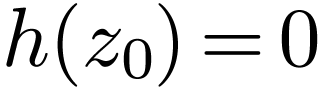 . Since
. Since 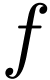 is bounded, we have
is bounded, we have 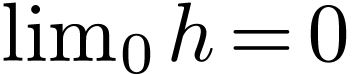 , so
, so 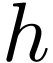 is
is  -differentiable
on
-differentiable
on 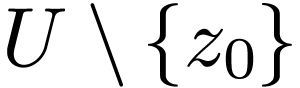 , so by the previous
theorem, the function
, so by the previous
theorem, the function 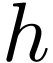 is
is  -differentiable at
-differentiable at  ,
with
,
with 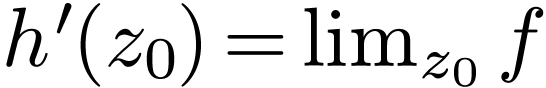 . We then extend
. We then extend 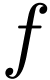 by continuity and see that
by continuity and see that 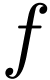 is
is
 -differentiable at
-differentiable at  .
.
Using the previous result and the maximum principle, one can prove the following:
Theorem 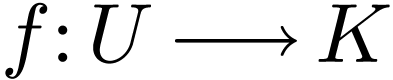 is definable and
is definable and  -differentiable,
then
-differentiable,
then 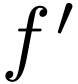 is also
is also  -differentiable.
-differentiable.
We start with an  -minimal
fact:
-minimal
fact:
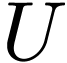 be open and non-empty. Let
be open and non-empty. Let 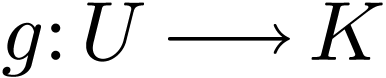 be definable, let
be definable, let 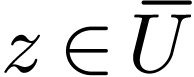 .
Then there is a neighborhood
.
Then there is a neighborhood 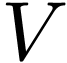 of
of 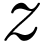 such that
such that 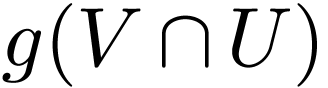 is not dense in
is not dense in 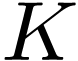 .
.
Proof. Assume for contradiction that this is not the
case. So for all 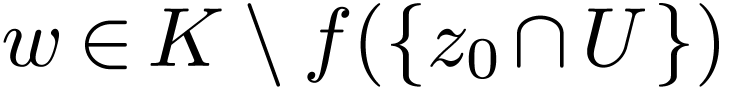 there is a definable path
there is a definable path  converging to
converging to  such that
such that 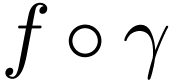 tends to
tends to 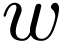 .
So
.
So 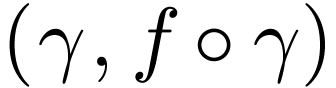 tends to
tends to 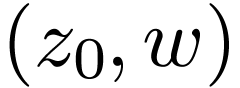 .
So
.
So 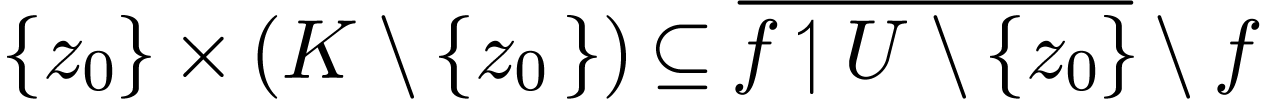 . But this is the frontier
of a set of dimension
. But this is the frontier
of a set of dimension  ,
whereas
,
whereas 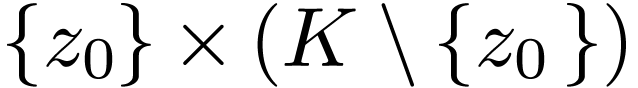 has dimension
has dimension  : a contradiction.
: a contradiction.
We fix an open set 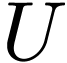 , a point
, a point
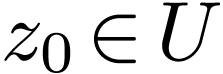 and a definable and
and a definable and 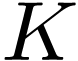 -differentiable
-differentiable 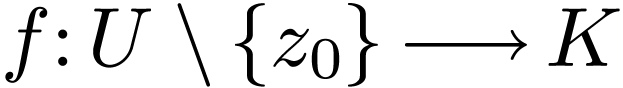 .
Assume that
.
Assume that 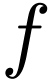 is not constant around
is not constant around  . We define the order
. We define the order 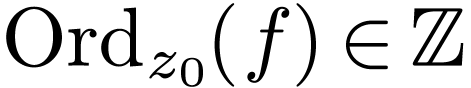 of
of 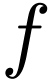 at
at  as
follows. Recall that for sufficiently large
as
follows. Recall that for sufficiently large 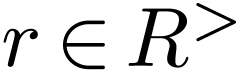 , the number
, the number 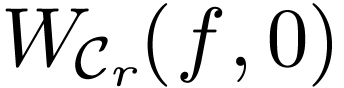 is constant
(where
is constant
(where 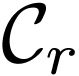 is the circle around
is the circle around  of radius
of radius 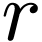 ). We then define
). We then define
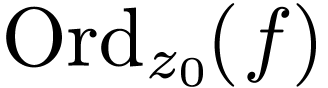 to be that integer.
to be that integer.
 is a removable singularity and
is a removable singularity and 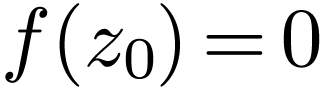
Write 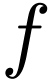 for the continuation on
for the continuation on 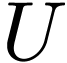 . We have
. We have 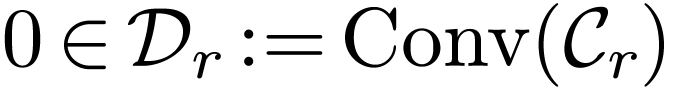 ,
whence
,
whence
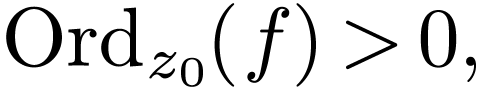
by a previous theorem.
 is a removable singularity and
is a removable singularity and 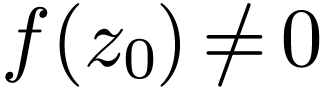
Again write 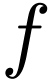 for the continuation on
for the continuation on 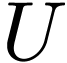 . If
. If 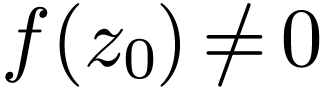 , then we claim that
, then we claim that
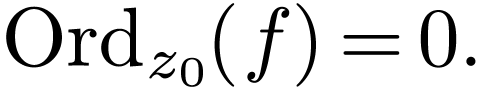
Indeed shrinking 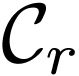 (hence
(hence 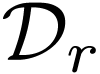 ) sufficiently, we can obtain that
) sufficiently, we can obtain that 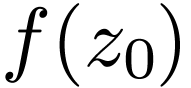 lie outside of
lie outside of 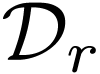 .
.
 is not removable
is not removable
In particular 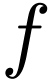 must be unbounded near
must be unbounded near  . We claim that
. We claim that
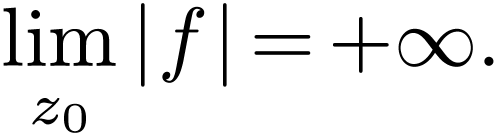 |
(3.1) |
Let 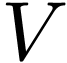 be a neighborhood of
be a neighborhood of  , let
, let 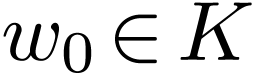 and
and 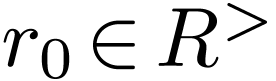 such that
such that
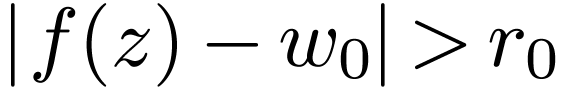 |
(3.2) |
for all 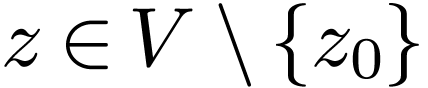 . Set
. Set
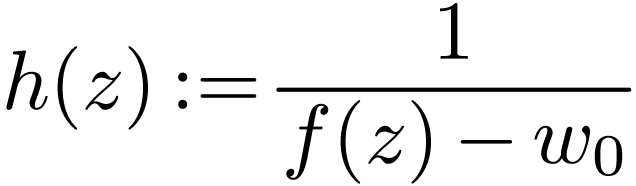
for all 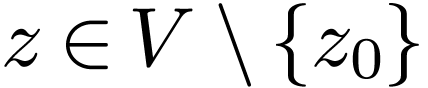 . The function
. The function
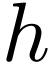 is
is 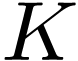 -differentiable,
and bounded by (3.2). So
-differentiable,
and bounded by (3.2). So  is a
removable singularity for
is a
removable singularity for 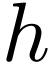 .
So
.
So 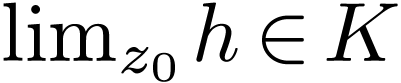 . We conclude since
. We conclude since
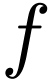 is unbounded near
is unbounded near  that
that 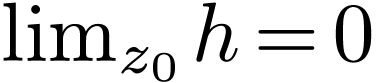 , whenc
, whenc 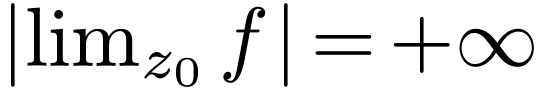 .
.
Let us show that
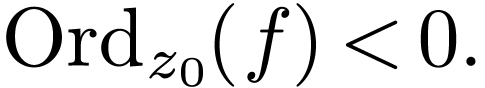
Set
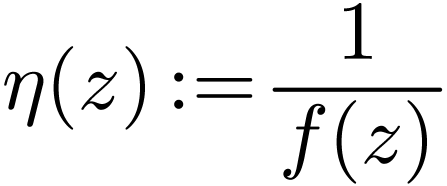
on a [épointé] neighborhood  of
of  .
By (3.1), we can extend
.
By (3.1), we can extend 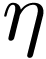 to
to
 by setting
by setting 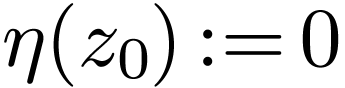 .
Now we know that
.
Now we know that 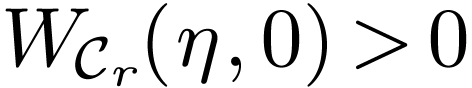 ,
whence
,
whence 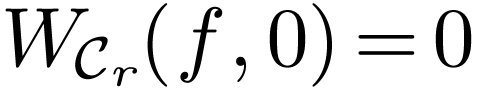 for all sufficiently small
for all sufficiently small 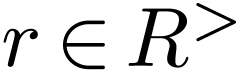 (i.e. whenever
(i.e. whenever 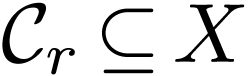 ).
).
Theorem 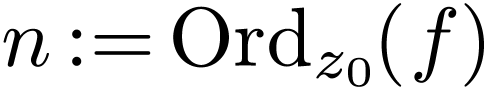 . There is a definable and
. There is a definable and
 -differentiable
-differentiable 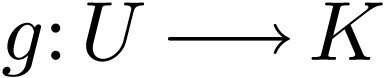 with
with 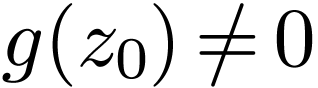 such that
such that
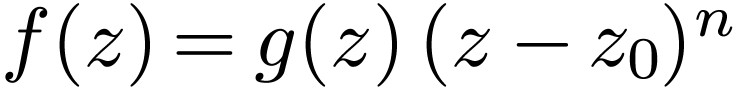
for all 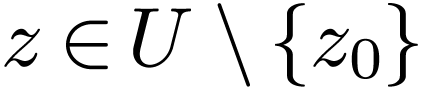 .
.
Proof. Let 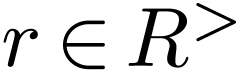 be sufficiently
small, so
be sufficiently
small, so 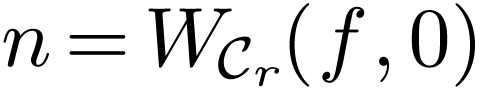 . Note that
. Note that 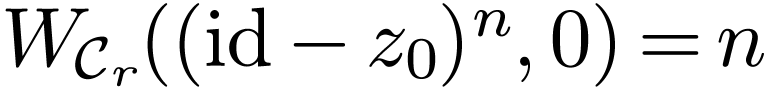 , so setting
, so setting 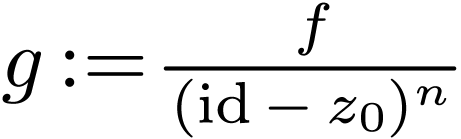 on
on 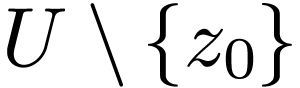 , we have
, we have 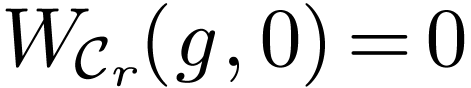 . By the previous trichotomy, the function
. By the previous trichotomy, the function 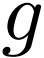 can be extended to
can be extended to  with
with 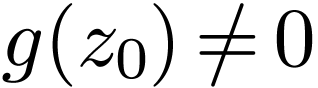 ; hence the result.
; hence the result.
Corollary  is
is  -differentiable
at
-differentiable
at  and that
and that 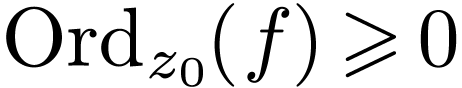 .
Then
.
Then 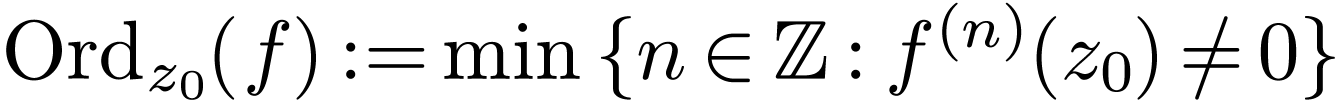 where
where 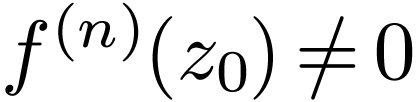 means that
there is an analytic continuation of
means that
there is an analytic continuation of 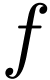 such
that...
such
that...
Corollary 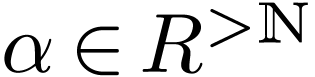 ,
“the” function
,
“the” function 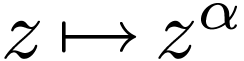 cannot be defined as
a
cannot be defined as
a  -differentiable map on a
neighborhood of
-differentiable map on a
neighborhood of  .
.
Let 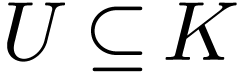 be a non-empty open definable set, and let
be a non-empty open definable set, and let
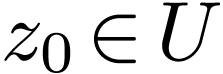 .
.
From the proof of Theorem 3.1, we deduce:
Theorem 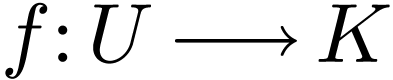 be definable and
be definable and  -differentiable.
Then
-differentiable.
Then
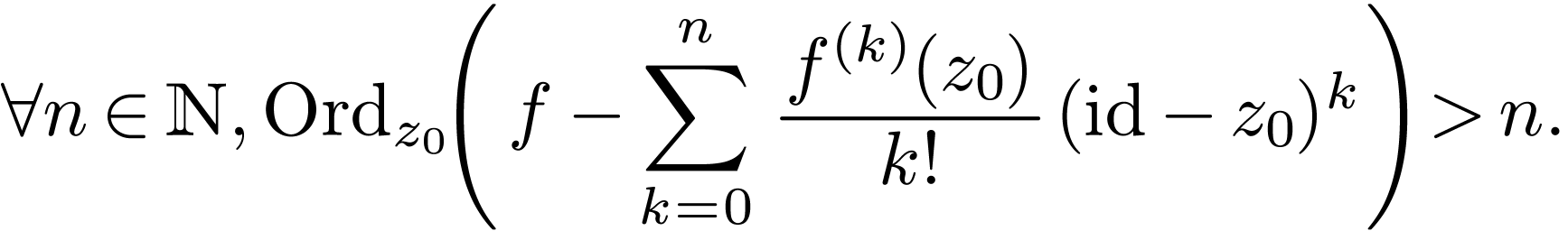
If  is a pole, then
is a pole, then
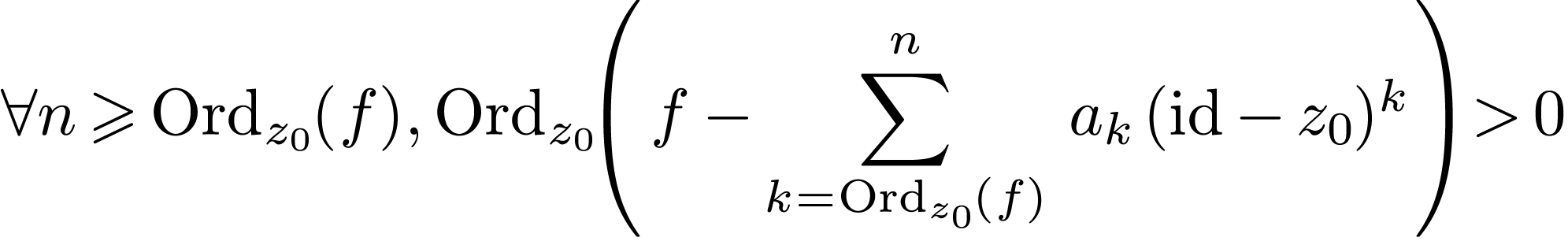
for a fixed sequence 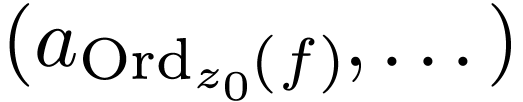 .
.
Corollary
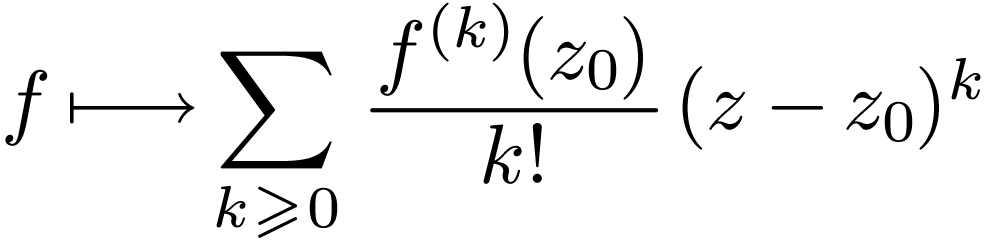
from germs at  of
of  -differentiable and definable functions to power
series in
-differentiable and definable functions to power
series in 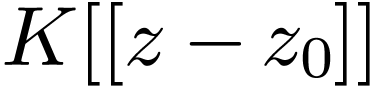 is injective.
is injective.
Theorem  -differentiable function
-differentiable function 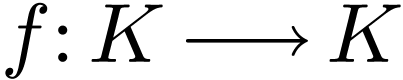 is a polynomial.
is a polynomial.
Theorem  is definable and
is definable and  -differentiable,
then
-differentiable,
then 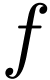 is a polynomial.
is a polynomial.
Proposition 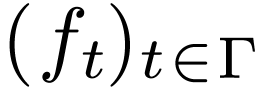 be a definable family of
be a definable family of  -differentiable
functions
-differentiable
functions  , then there is an
, then there is an
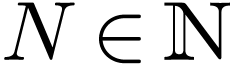 such that each
such that each 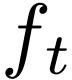 has
degree
has
degree  .
.
Question 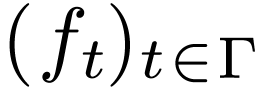 be a definable family of polynomial functions on
be a definable family of polynomial functions on 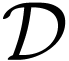 . Is there a uniform bound on the degree of
. Is there a uniform bound on the degree of 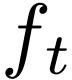 ?
?
Example 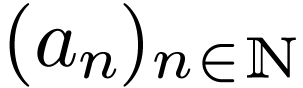 be an arbitrary sequence of
complex numbers in
be an arbitrary sequence of
complex numbers in 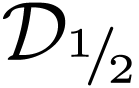 with absolute value
with absolute value 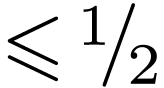 . Define
. Define
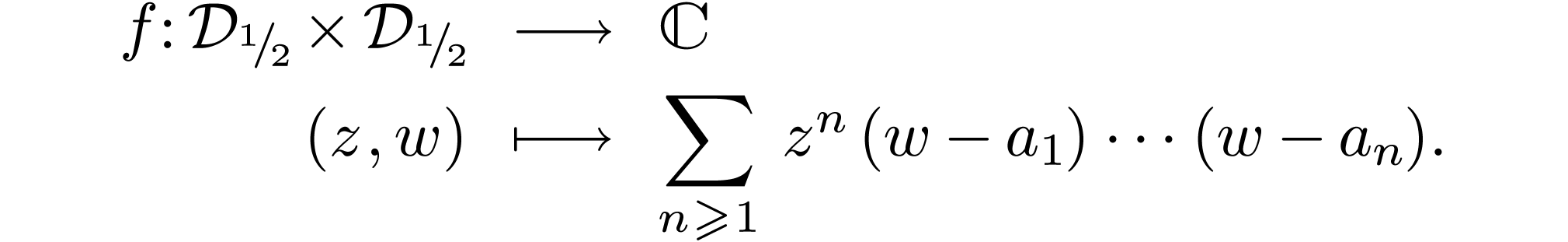
This is definable in 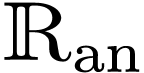 , and
for all
, and
for all 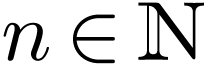 , the function
, the function 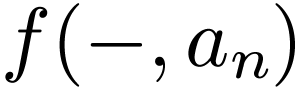 is a polynomial of degree
is a polynomial of degree 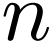 . But for
. But for 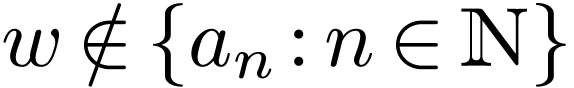 the function
the function 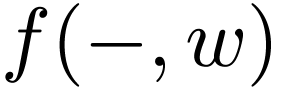 is not a polynomial, so this doesn't give a negative
answer to the previous question.
is not a polynomial, so this doesn't give a negative
answer to the previous question.
Proposition 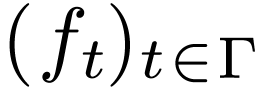 be a definable family of
be a definable family of  -differentiable
functions on
-differentiable
functions on 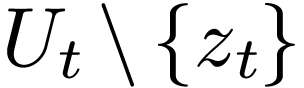 for open sets
for open sets 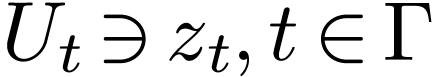 . Then there is an
. Then there is an 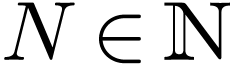 , such that for all
, such that for all 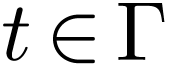 ,
either
,
either 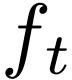 is locally constant around
is locally constant around 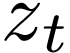 or
or 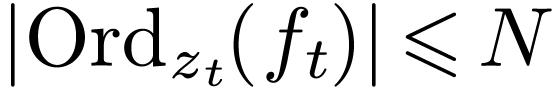 .
.
Proposition 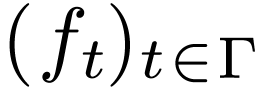 be a definable family of
be a definable family of  -differentiable
functions on
-differentiable
functions on  for open sets
for open sets  . For
. For 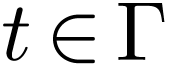 ,
let
,
let
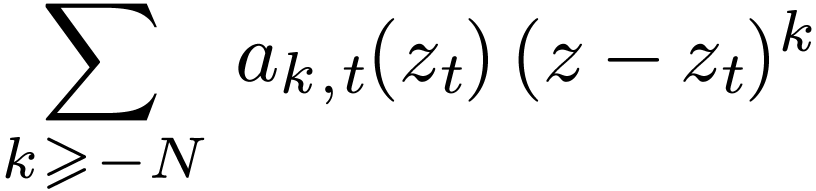
be the Laurent series associated to 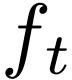 ,
where
,
where 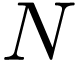 is as in the previous proposition. Then
the function
is as in the previous proposition. Then
the function
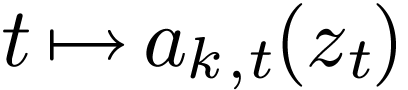
is definable.
Let us now go back to the classical setting 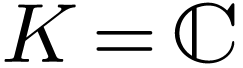 . Let
. Let 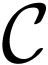 be a simple closed
curve and let
be a simple closed
curve and let 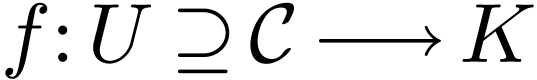 have finitely many residues
have finitely many residues  in
in  .
Recall that
.
Recall that 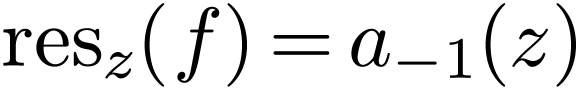 in the previous notations. We have
in the previous notations. We have
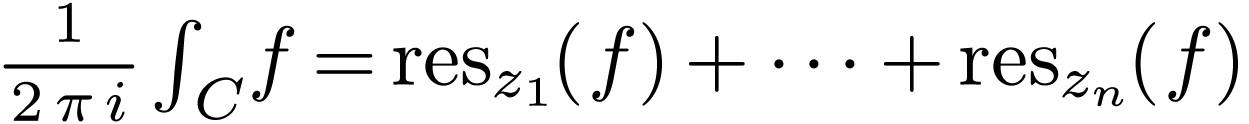 .
.
So if  is as above and
is as above and  is
a definable family of simple closed curves, and
is
a definable family of simple closed curves, and 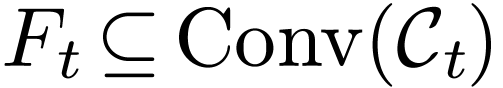 is finite and uniformly definable, then the function
is finite and uniformly definable, then the function
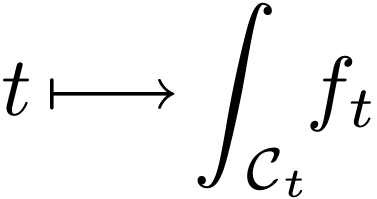
is also definable.
Theorem 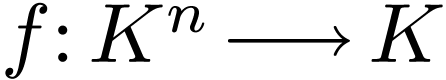 is definable and
is definable and  -differentiable,
then
-differentiable,
then 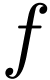 is polynomial.
is polynomial.
Proof. For all 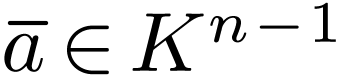 ,
the function
,
the function 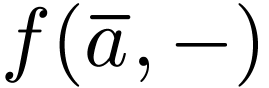 is polynomial by the one variable
corresponding result. By
is polynomial by the one variable
corresponding result. By  -minimality,
the degrees of corresponding polynomials when
-minimality,
the degrees of corresponding polynomials when 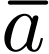 ranges in
ranges in 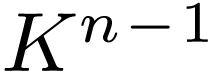 are bounded by some
are bounded by some 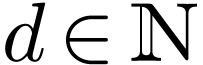 . So
. So 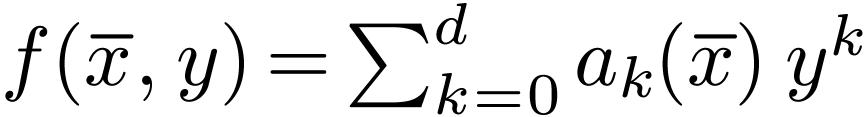 .
Loooking at
.
Loooking at 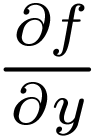 , we can conclude
by induction.
, we can conclude
by induction.
In fact, we have a result from 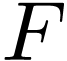 and
and 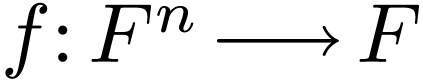 which is polynomial in each variable, the function
which is polynomial in each variable, the function 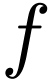 is in fact polynomial.
is in fact polynomial.
Assume that 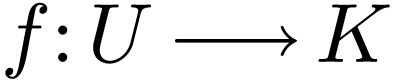 is definable and
is definable and 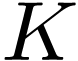 -differentiable on a non-empty open set
-differentiable on a non-empty open set 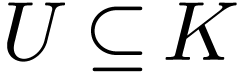 , and let
, and let 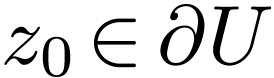 such that
such that  is simply connected for some
neighborhood
is simply connected for some
neighborhood 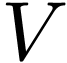 of
of  .
Then
.
Then 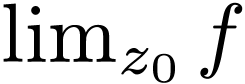 exists in
exists in 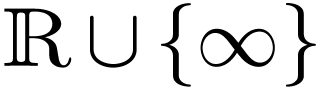 .
Indeed recall that for
.
Indeed recall that for 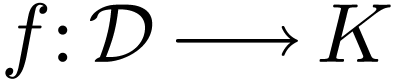 definable, and
non-constant and
definable, and
non-constant and 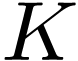 -differentiable
on
-differentiable
on 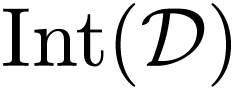 , then
, then 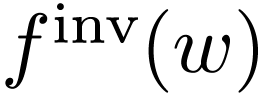 is finite on
is finite on 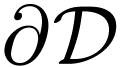 . Indeed assume
that
. Indeed assume
that 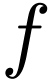 as infinitely many limit points around
as infinitely many limit points around
 . Then sufficiently close to
. Then sufficiently close to
 , one can also arrange that
, one can also arrange that
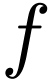 is injective and that it have non-zero
derivative. So the inverse map of the restriction will be
is injective and that it have non-zero
derivative. So the inverse map of the restriction will be 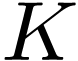 -differentiable on an open set. Then
-differentiable on an open set. Then 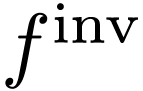 sends an infinite subset of
sends an infinite subset of 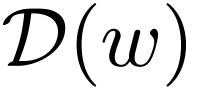 to
to
 , so
, so 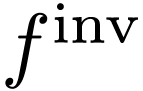 must be constant: a contradiction.
must be constant: a contradiction.
Question 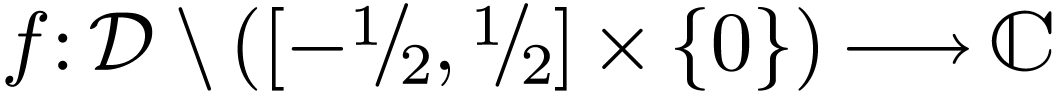 is holomorphic and bounded. Does
is holomorphic and bounded. Does 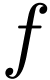 extend to
extend to 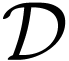 ?
(preserving boundedness).
?
(preserving boundedness).
We now work with 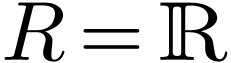 , so
, so 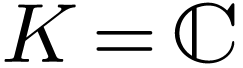 . Apparently the results should
still be valid in the more general context.
. Apparently the results should
still be valid in the more general context.
Definition  -manifold is
-manifold is
a definable 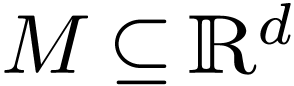 ,
,
a finite cover by definable subsets 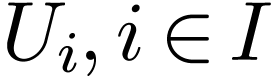 ,
,
For all 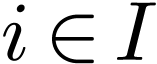 , a definable
bijection
, a definable
bijection 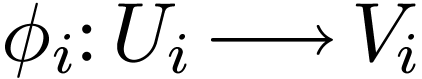 into an open subset
into an open subset 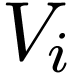 of
of  such that the transition
maps are holomorphic.
such that the transition
maps are holomorphic.
Note that the transition maps are definable.
Example 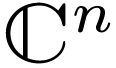 ,
graphs of definable holomorphic maps
,
graphs of definable holomorphic maps
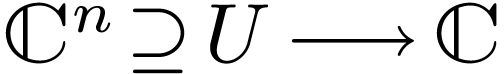 ,
as well as the projective spaces are definable manifolds. If
,
as well as the projective spaces are definable manifolds. If
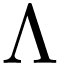 is a discrete sugroup of
is a discrete sugroup of
 ,
then the quotient
,
then the quotient
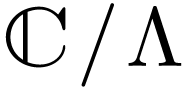 can be equipped with a
can be equipped with a
 -manifold
chart by realizing this within
-manifold
chart by realizing this within

7.1. this speaks to Lou's remark being relevant: can we not define this abstractly rather than always having to find a embedded representation?
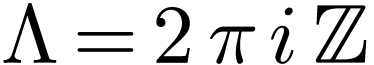 ,
and define
,
and define
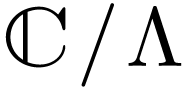 to be
to be
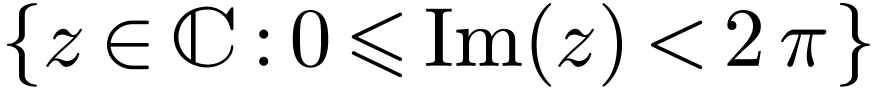 .
We then give the two usual charts. If we are working in
.
We then give the two usual charts. If we are working in
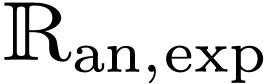 in the language, then the complex exponential is definable on small
strips on
in the language, then the complex exponential is definable on small
strips on
 ,
so we can realize
,
so we can realize
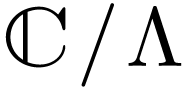 as a definable “holomorphic” copy of
as a definable “holomorphic” copy of
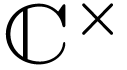 .
.
Fact: Every compact analytic manifold is definably
biholomorphic (in the sense of manifolds) to a definable  -manifold.
-manifold.
Definition 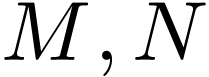 definable
definable  -manifolds.
A definable holomorphic function
-manifolds.
A definable holomorphic function  is a definable
function
is a definable
function 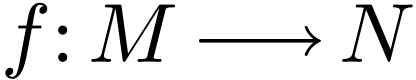 which is holomorphic through
charts.
which is holomorphic through
charts.
Definition 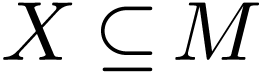 which is an
which is an
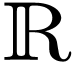 -submanifold, for which
moreover the tangent space at each
-submanifold, for which
moreover the tangent space at each 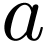 is
is  -linear.
-linear.
The only compact definale submanifolds of  are
the finite sets.
are
the finite sets.
Theorem 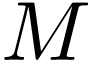 be a definable
be a definable  -manifold.
If
-manifold.
If 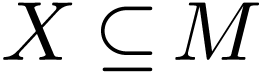 is a definable submanifold, then it has a
natural structure of definable
is a definable submanifold, then it has a
natural structure of definable  -manifold,
and the inclusion
-manifold,
and the inclusion 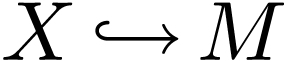 is a definable holomorphic
function.
is a definable holomorphic
function.
Definition 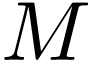 be a definable
be a definable  -manifold.
A definable analytic subset of
-manifold.
A definable analytic subset of 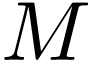 is a definable
closed
is a definable
closed 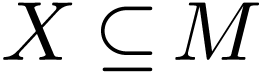 such that for all
such that for all 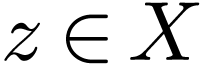 , there are a definale neighorhood
, there are a definale neighorhood 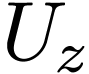 of
of 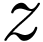 and finitely many definable and holomorphic
functions
and finitely many definable and holomorphic
functions 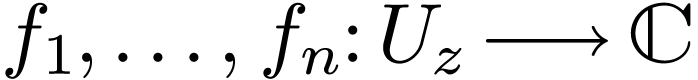 with
with
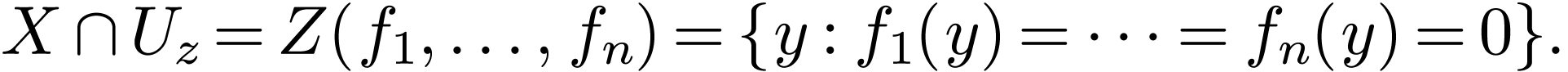
It can be showed that in fact  can be covered by
finitely many such sets
can be covered by
finitely many such sets  and functions.
and functions.
Example 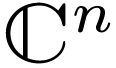 are definable analytic subsets of
are definable analytic subsets of  . If
. If 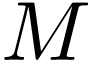 is a
definable compact
is a
definable compact  -manifold
for
-manifold
for 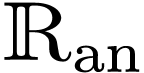 , then every analytic
subset of
, then every analytic
subset of 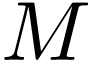 is a definable analytic subset of
is a definable analytic subset of 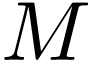 (again in
(again in 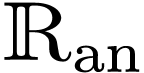 ).
).
(By Chow's theorem, every analytic subset of 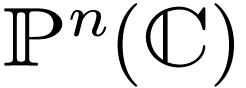 is
an algebraic variety.)
is
an algebraic variety.)
The basic problem: 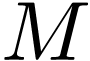 is a definable
is a definable  -manifold, we have a definable open
-manifold, we have a definable open 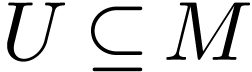 , and a definable analytic subset
, and a definable analytic subset
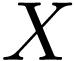 of
of 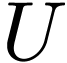 as per Definition 7.6. When is the closure
as per Definition 7.6. When is the closure 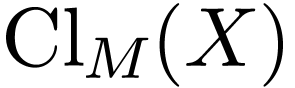 of
of 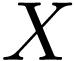 in
in 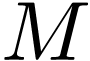 an analytic subset of
an analytic subset of 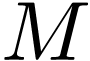 ? So did we “add
singularities” by taking the closure?
? So did we “add
singularities” by taking the closure?
Example 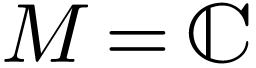 and take
and take 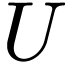 to be the unit disk. So
to be the unit disk. So 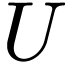 is a definable analytic subset of itself. But the closed
disk is not an analytic subset of
is a definable analytic subset of itself. But the closed
disk is not an analytic subset of  .
.
We recall a classical result of removal of singularities:
Remmert-Stein theorem. Let 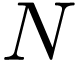 be a
be a  -manifold, let
-manifold, let 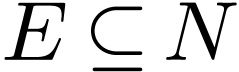 be a
be a  -analytic
subset, and set
-analytic
subset, and set 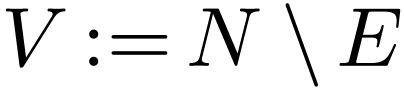 . If
. If 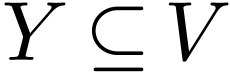 is irreducible analytic subset, and
is irreducible analytic subset, and 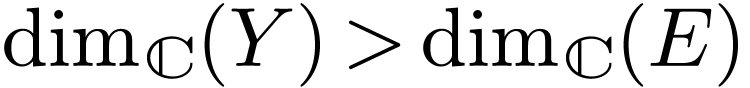 , then
, then 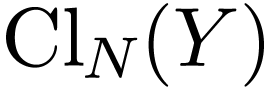 is an analytic
subset of
is an analytic
subset of 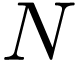 .
.
A bunch of 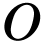 -minimal ROS
results:
-minimal ROS
results:
Assume that 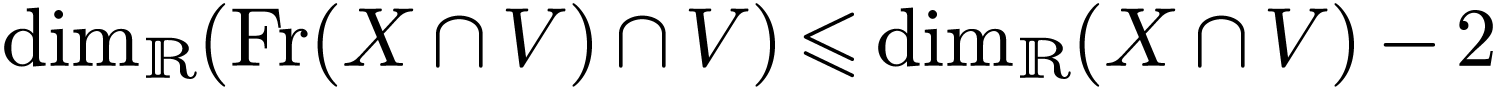 for all non-empty definable open
for all non-empty definable open
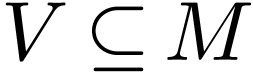 . Then
. Then 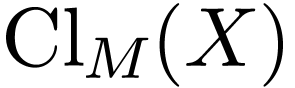 is an analytic susbet of
is an analytic susbet of 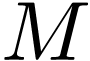 .
.
Let 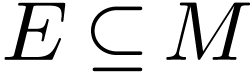 be a definable analytic subset with
be a definable analytic subset with
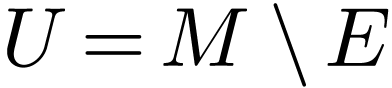 . Then
. Then 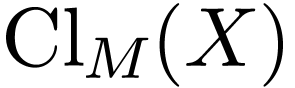 is an analytic susbet of
is an analytic susbet of 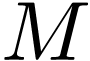 .
.
A corollary of  is that
is that
Corollary 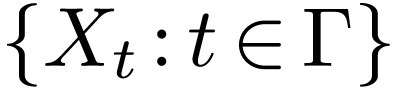 is a definable family of subsets of a definable
is a definable family of subsets of a definable  -manifold
-manifold 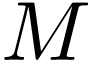 , then the set
, then the set 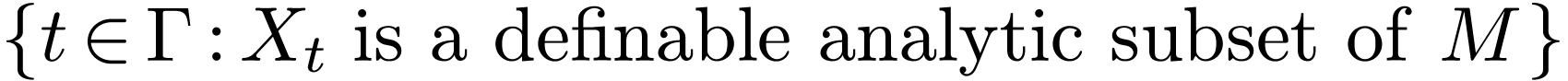 is
definable.
is
definable.
Proof. Set 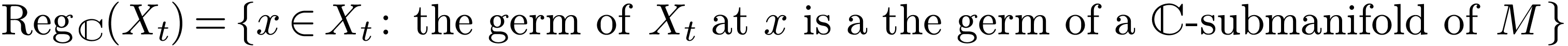 for each
for each 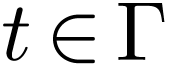 . Each
. Each 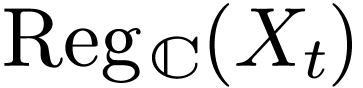 is a
locally analytic definable subset of
is a
locally analytic definable subset of 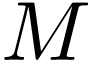 .
The set
.
The set 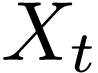 is an analytic subset of
is an analytic subset of 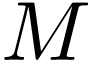 if and only if
if and only if 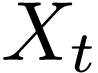 is closed, if
is closed, if 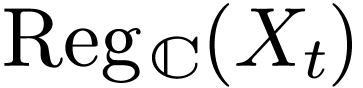 is dense in
is dense in 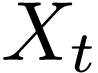 ,
and if
,
and if 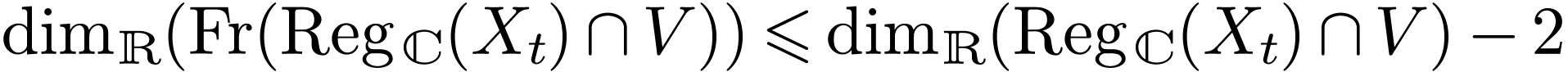 for all non-empty definable open
for all non-empty definable open 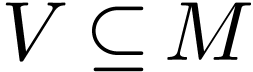 .
.
It follows that we have a:
Definable Chow theorem. If 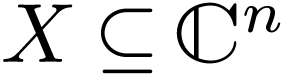 is a definable analytic subset, then
is a definable analytic subset, then 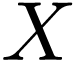 is
algebraic.
is
algebraic.
Corollary 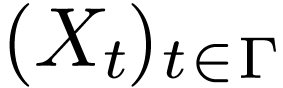 is a definable family of subsets of
is a definable family of subsets of 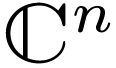 , then
, then 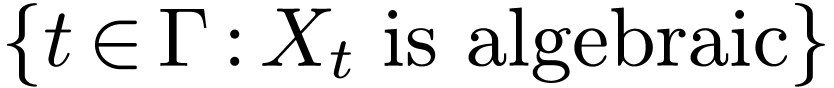 is definable.
is definable.
Exercise  -minimal structures.
-minimal structures.
Assume that we have a lattice 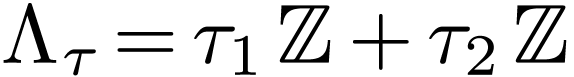 where
where 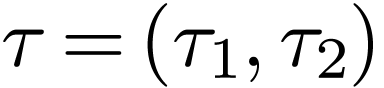 is an
is an 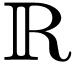 -basis of
-basis of
 . Write
. Write 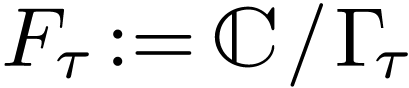 with its definable structure of
with its definable structure of  -manifold.
Then we saw that
-manifold.
Then we saw that 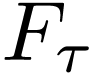 is isomorphic to an elliptic
curve
is isomorphic to an elliptic
curve 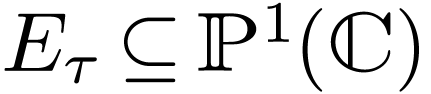 .
.
We may assume that 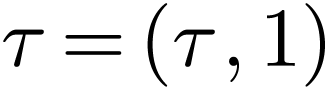 where
where 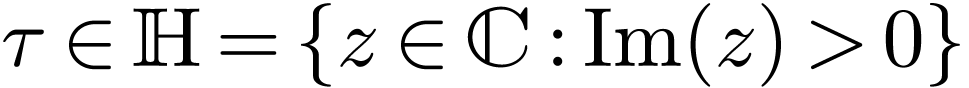 . Recall that
. Recall that 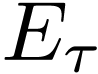 and
and 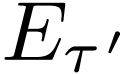 are isomorphic if and only if there is a
are isomorphic if and only if there is a 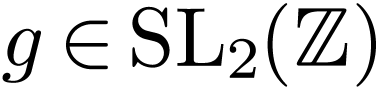 with
with 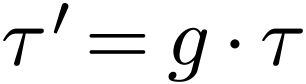 (where
(where  is the
standard action of
is the
standard action of 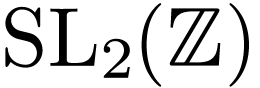 on
on  ). Moreover, there is a holomorphic and
transcendental surjective map
). Moreover, there is a holomorphic and
transcendental surjective map 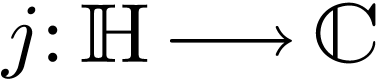 with
with
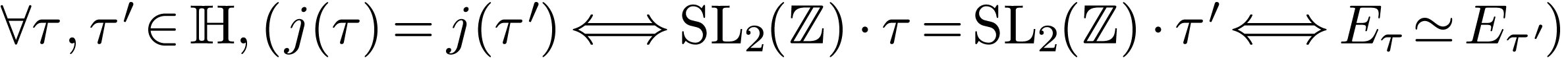
where the isomorphism is as abelian varieties, analytic manifolds. The
function 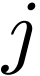 is called the
is called the 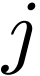 invariant.
invariant.
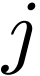
Set
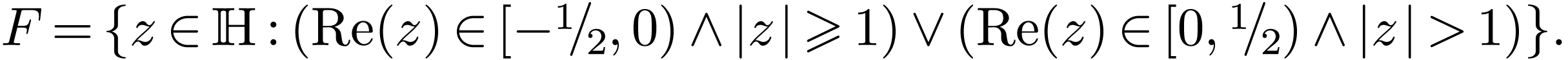
Then each orbit of  has excatly one
representative in
has excatly one
representative in 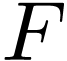 . It
follows that
. It
follows that 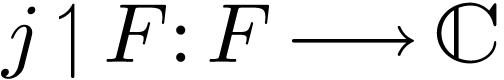 is still surjective (and
injective).
is still surjective (and
injective).
Theorem 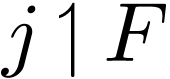 is definale in
is definale in 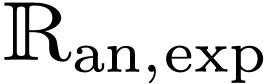 .
.
Proof. Consider the function 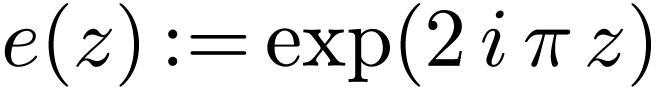 . Then
. Then 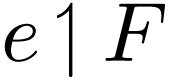 is definable in
is definable in 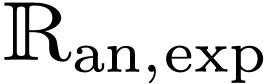 by previous results. Now on any bounded part
by previous results. Now on any bounded part 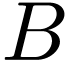 of
of 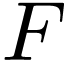 , the
function
, the
function 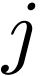 is definable on
is definable on  in
in 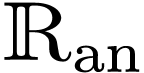 . For
. For 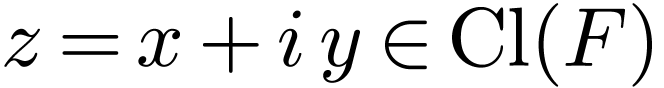 , we have
, we have 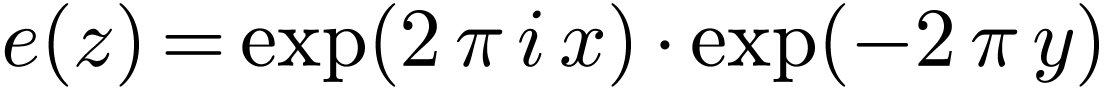 ,
and we see that
,
and we see that 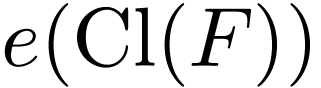 is the punctured disk
is the punctured disk 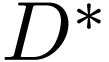 centered on
centered on 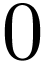 .
Recall that in particular
.
Recall that in particular 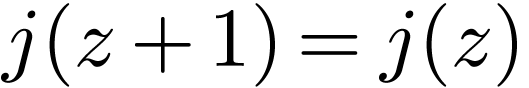 for all
for all 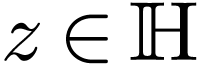 , and
, and 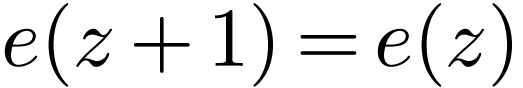 as well. So we
can factor
as well. So we
can factor 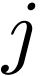 by
by 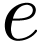 and get an
analytic map
and get an
analytic map 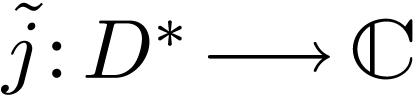 with
with
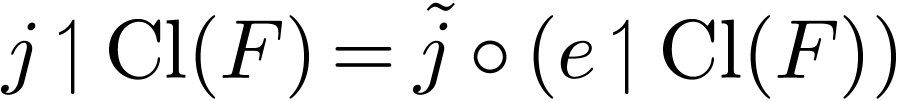
Fact: 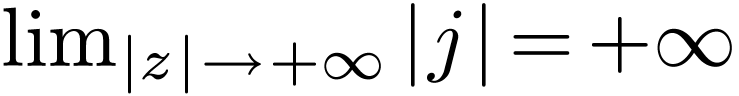 , so
, so 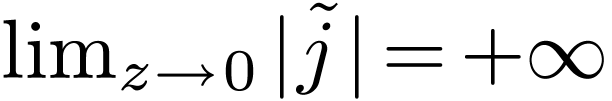 , i.e.
, i.e. 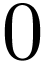 is a pole of
is a pole of
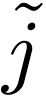 , and we can write
, and we can write 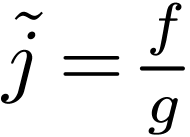 where
where 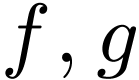 are analytic, definable in
are analytic, definable in
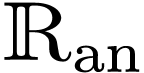 . So
. So 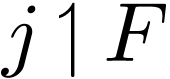 is definable in
is definable in 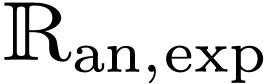 .
.