On Hardy fields and models of 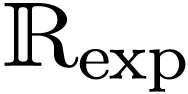 |
|
| April 2022 |
|
I write 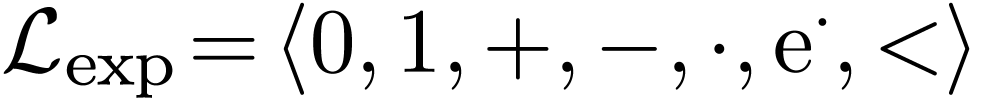 for the language of ordered exponential
rings,
for the language of ordered exponential
rings, 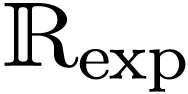 for the the real ordered exponential
field, and
for the the real ordered exponential
field, and 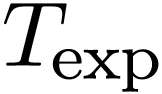 for its elementary theory. Recall
that
for its elementary theory. Recall
that 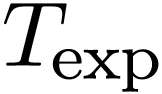 is model complete in
is model complete in 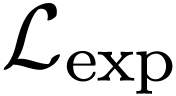 by Wilkie's theorem, and that
by Wilkie's theorem, and that 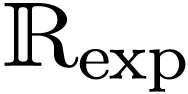 is o-minimal.
is o-minimal.
I start with a few preliminary results that I actually didn't know were true in general.
Lemma 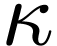 be an infinite cardinal and let
be an infinite cardinal and let 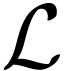 be a first-order language. An
be a first-order language. An 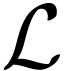 -structure
-structure
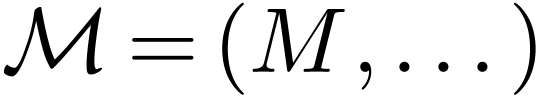 is
is 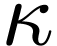 -saturated
if and only if for all subsets
-saturated
if and only if for all subsets 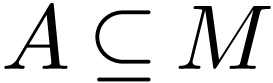 with
with 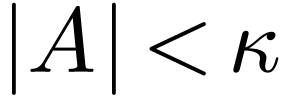 , all
, all  -types
-types
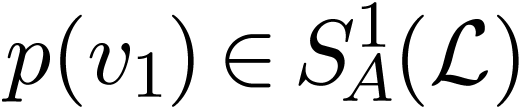 over
over  are satisfiable in
are satisfiable in
 .
.
Proposition 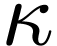 be an infinite cardinal. Let
be an infinite cardinal. Let 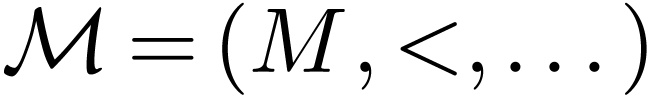 be an
be an
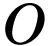 -minimal structure with such
that
-minimal structure with such
that 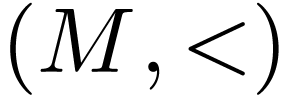 is a dense linear order without endpoints.
Assume that for all subsets
is a dense linear order without endpoints.
Assume that for all subsets 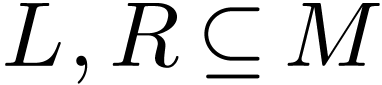 with cardinality
with cardinality
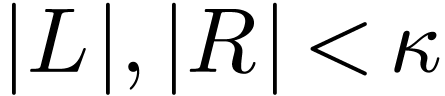 and with
and with 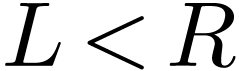 ,
there is an
,
there is an 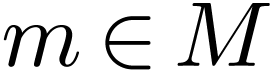 with
with 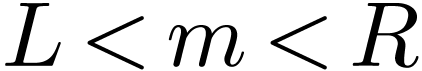 .
Then
.
Then 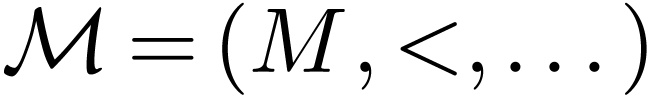 is
is  -saturated.
-saturated.
Corollary  be an infinite uncountable cardinal. The ordered
exponential field
be an infinite uncountable cardinal. The ordered
exponential field 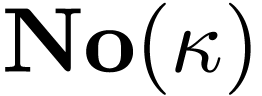 of surreal numbers of length /
birth day
of surreal numbers of length /
birth day  with Gonshor's exponential function is
with Gonshor's exponential function is
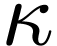 -saturated.
-saturated.
Proof. The underlying ordered set is 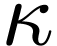 -saturated by definition of surreal numbers and
by a simple fact (found in [1, Chapter 1]): if
-saturated by definition of surreal numbers and
by a simple fact (found in [1, Chapter 1]): if 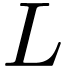 and
and 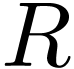 are sets of surreal numbers
with
are sets of surreal numbers
with 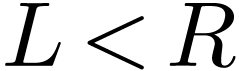 , then the simplest
number
, then the simplest
number 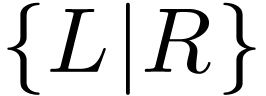 with
with

has birthday 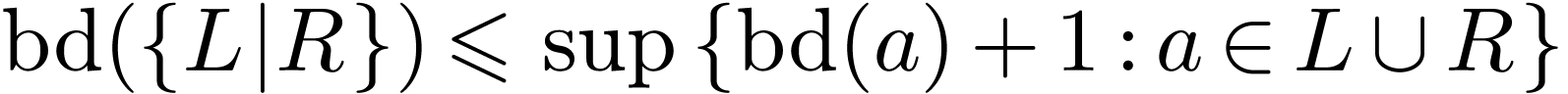 .
.
We also know, by a result of Ehrlich and van den Dries [2],
that 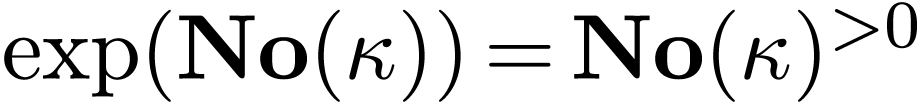 and that
and that  can be
expanded into a model of
can be
expanded into a model of 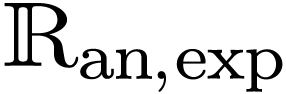 .
Thus
.
Thus 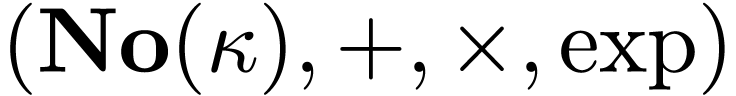 is o-minimal.
is o-minimal.
Corollary  elementarily embeds into a
elementarily embeds into a  for large enough
for large enough 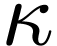 .
.
I was asking myself the following questions:
Question 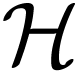 be a Hardy field containing
be a Hardy field containing 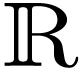 . Assume that
. Assume that 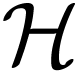 is real-closed
and closed under
is real-closed
and closed under 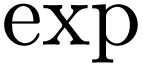 and
and 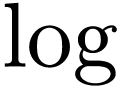 . Is
. Is 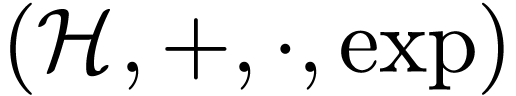 an elementary expansion
of
an elementary expansion
of 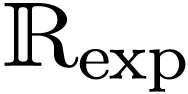 ?
?
Question 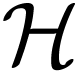 be a Hardy field containing
be a Hardy field containing 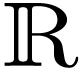 and closed under
and closed under 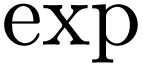 . Does
. Does 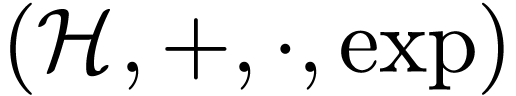 embed into an elementary extension of
embed into an elementary extension of 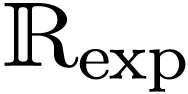 ?
?
Lou found answers to those questions, which I next explain.
In order to answer the first question, in the negative, we require three objects:
We write 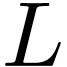 for Hardy's field of
logarithmico-exponential functions, i.e. germs at
for Hardy's field of
logarithmico-exponential functions, i.e. germs at  that can be obtained as compositions of
that can be obtained as compositions of  ,
, 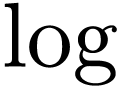 ,
and semialgebraic functions
,
and semialgebraic functions  .
In other words, this is the closure of the field
.
In other words, this is the closure of the field 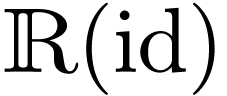 of rational functions under real closure,
of rational functions under real closure, 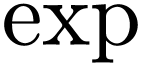 and
and
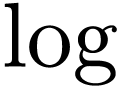 , which Hardy showed to be a
Hardy field.
, which Hardy showed to be a
Hardy field.
Let 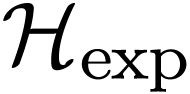 denote the Hardy field of germs at
denote the Hardy field of germs at 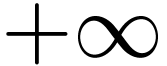 of
of 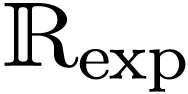 -definable
functions
-definable
functions  , allowing
parameters. Note that given a positive infinite germ
, allowing
parameters. Note that given a positive infinite germ 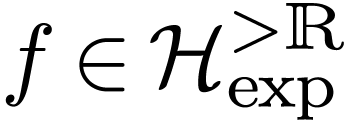 , its functional inverse
, its functional inverse 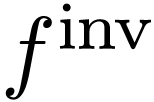 is also definable with parameters in
is also definable with parameters in 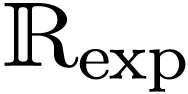 ,
so
,
so 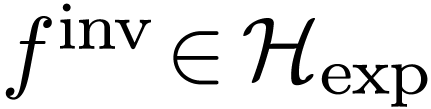 .
.
Let 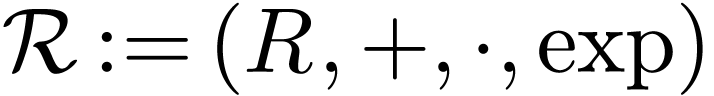 be non-standard, i.e. a proper elementary
extension of
be non-standard, i.e. a proper elementary
extension of 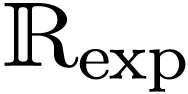 . Fix an
. Fix an 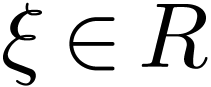 with
with 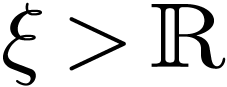 .
This exists since
.
This exists since 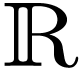 is the largest archimedean
ordered field.
is the largest archimedean
ordered field.
Proposition 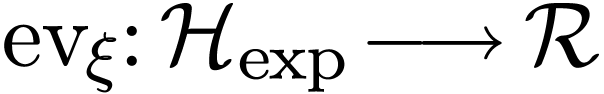 which commutes with
which commutes with
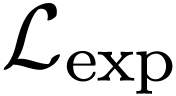 -definable functions
-definable functions 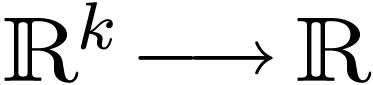 /
/ 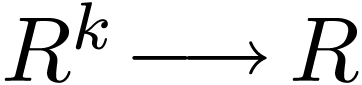 with parameters in
with parameters in 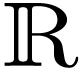 and sends the germ
and sends the germ 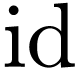 of the
identity function onto
of the
identity function onto  .
.
Proof. Cheking all details is a bit tedious but I think
this is a well-known result. I just give the definition. Fix a
representative 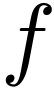 of a germ in
of a germ in 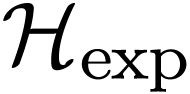 . There is a defining formula
. There is a defining formula 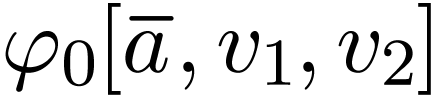 for
for 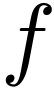 with parameters
with parameters 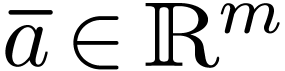 and
a real number
and
a real number 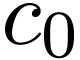 such that for all
such that for all 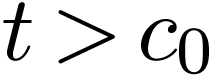 , the number
, the number 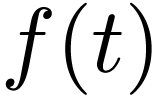 is unique
with
is unique
with 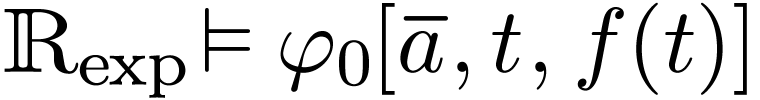 . Let
. Let 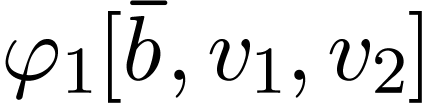 be a second defining formula with parameters
be a second defining formula with parameters 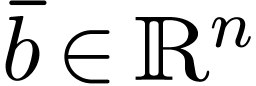 satisfying the same relation, with respect to the same germ, for a
possibly distinct
satisfying the same relation, with respect to the same germ, for a
possibly distinct 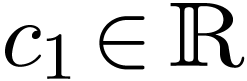 . In
particular, we have
. In
particular, we have
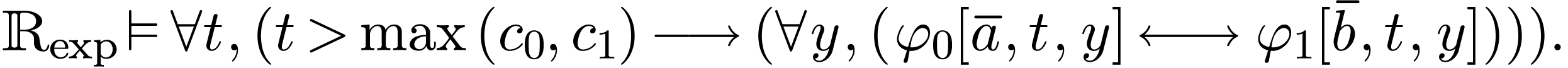 |
(1) |
Recall that 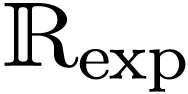 is o-minimal, so
is o-minimal, so  is an elementary embedding. We have
is an elementary embedding. We have 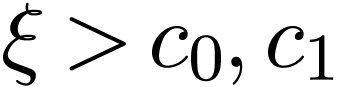 ,
so by (1), the unique element
,
so by (1), the unique element 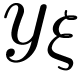 of
of
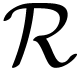 with
with  is also the unique
element of
is also the unique
element of 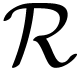 satisfying
satisfying 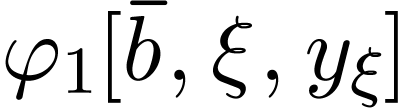 . We define
. We define 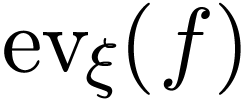 to be that
element
to be that
element 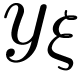 .
.
Similar arguments show that 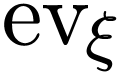 commutes with
commutes with 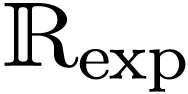 -definable functions
-definable functions  , whence in particular that it is an embedding
in
, whence in particular that it is an embedding
in 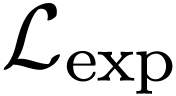 , hence an elementary
embedding by model completeness.
, hence an elementary
embedding by model completeness.
Proposition 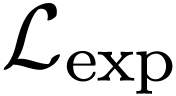 -embedding of
-embedding of 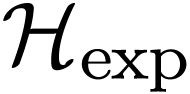 into
into 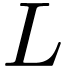 .
.
Proof. Assume for contradiction that there is such an
embedding 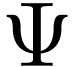 and write
and write 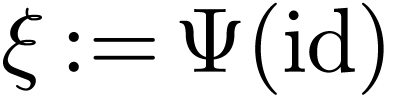 . The field
. The field 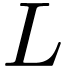 is contained in
is contained in
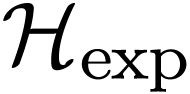 , and since
, and since 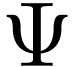 must commute with semialgebraic functions as well as with
must commute with semialgebraic functions as well as with 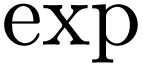 and
and 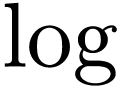 , we have
, we have
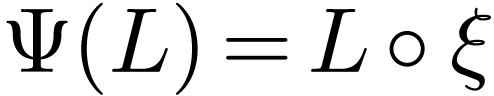 . For the same reasons, we
have
. For the same reasons, we
have 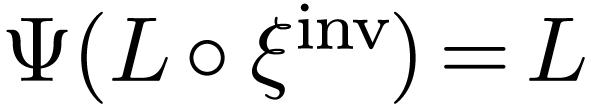 . The function
. The function 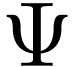 is injective, so
is injective, so 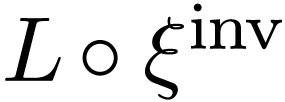 must coincide
with
must coincide
with 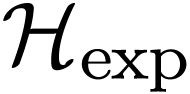 , whence in
, whence in 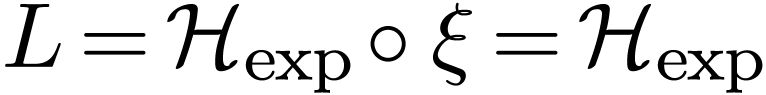 . But this is known to be false: for instance
it is a theorem of van den Dries, Macintyre and Marker that the germ
. But this is known to be false: for instance
it is a theorem of van den Dries, Macintyre and Marker that the germ
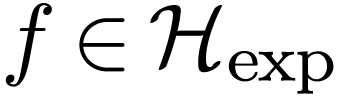 of the functional inverse of
of the functional inverse of 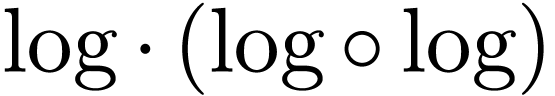 does not lie in
does not lie in 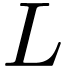 .
.
This raises a question:
Question 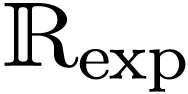 ? Is there an H-closed Hardy field which is a model
of
? Is there an H-closed Hardy field which is a model
of 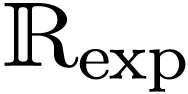 ?
?
The answer to the second question is positive. In order to 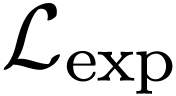 -embed
-embed 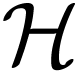 into an
elementary extension of
into an
elementary extension of 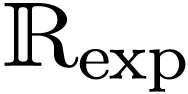 , it
is enough, since
, it
is enough, since 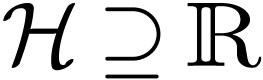 and by model completeness, to
construe it as a substructure of a model of
and by model completeness, to
construe it as a substructure of a model of 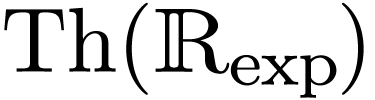 .
.
Proposition 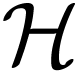 be a Hardy field containing
be a Hardy field containing 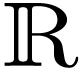 and closed under
and closed under 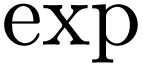 . Then
. Then 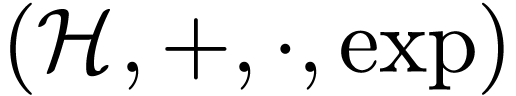 embeds into an elementary extension of
embeds into an elementary extension of 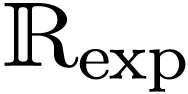 .
.
Proof. We need to prove that 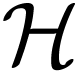 is
a model of the universal theory
is
a model of the universal theory 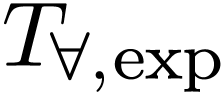 of
of 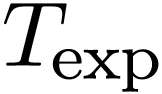 . Consider a universal formula
. Consider a universal formula 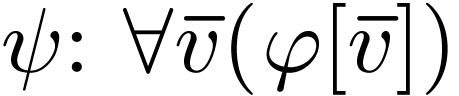 where
where 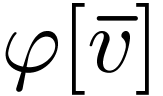 is a boolean combination of atomic
is a boolean combination of atomic 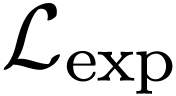 -formulas, hence, up to equivalence
modulo the theory of rings, of exponential-polynomial equations,
inequations, inequalities... We can assume that
-formulas, hence, up to equivalence
modulo the theory of rings, of exponential-polynomial equations,
inequations, inequalities... We can assume that 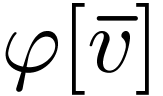 is in disjunctive conjunctive form
is in disjunctive conjunctive form
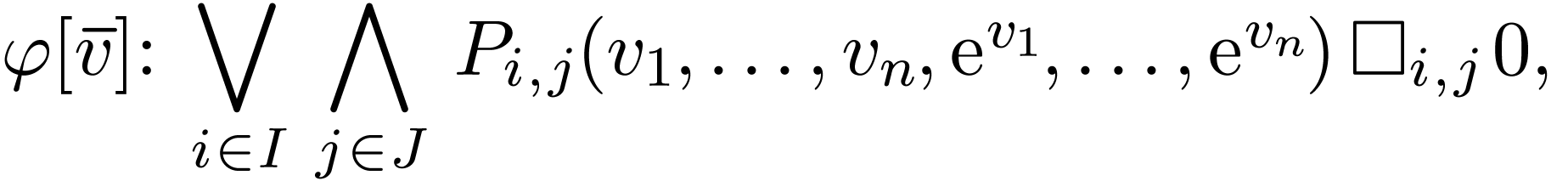
where each 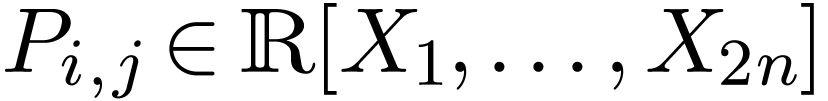 , each symbol
, each symbol 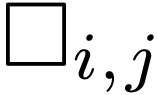 is among
is among 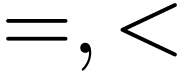 ,
and
,
and 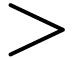 , and
, and 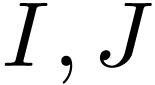 are finite sets.
are finite sets.
Assume that 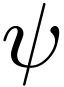 is valid in
is valid in 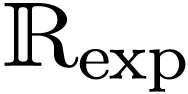 and let
and let  be representatives of germs in
be representatives of germs in 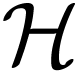 . Since
. Since 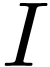 is
finite, there are a cofinal subset
is
finite, there are a cofinal subset 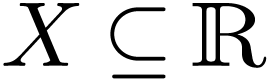 and an
and an 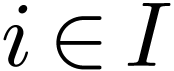 for which we have
for which we have
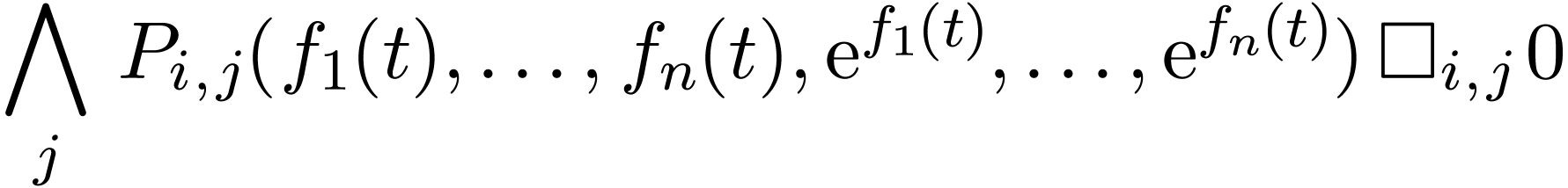
whenever 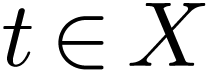 . Since
. Since  is a Hardy field, the sign of each function
is a Hardy field, the sign of each function
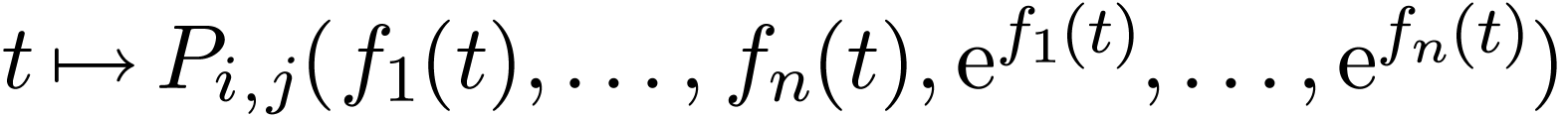
for 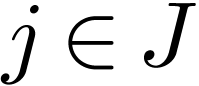 is stationnary. So we actually have
is stationnary. So we actually have 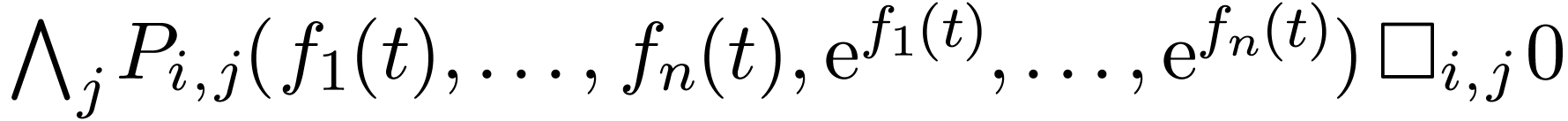 for all sufficiently large
for all sufficiently large 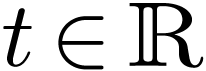 . This means that
. This means that 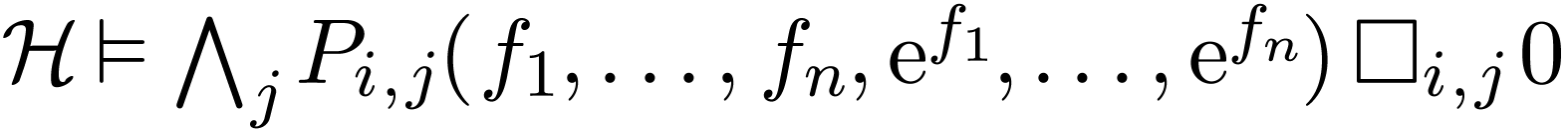 ,
whence in particular that
,
whence in particular that 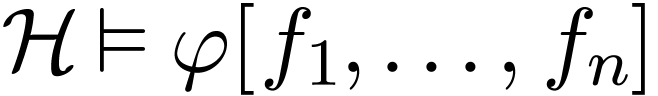 .
Therefore
.
Therefore 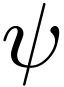 is valid in
is valid in 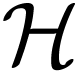 . This shows that
. This shows that 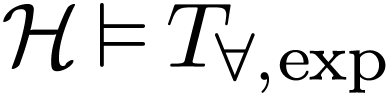 embeds
into a model of
embeds
into a model of 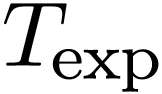 .
.
Corollary 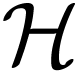 closed under
closed under 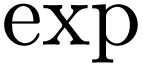 embeds into
embeds into
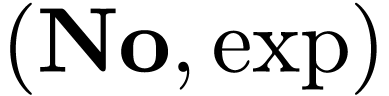 as an ordered exponential field.
as an ordered exponential field.
Proof. We first embed 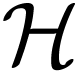 into a
Hardy field
into a
Hardy field 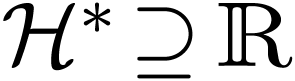 which is closed under
which is closed under 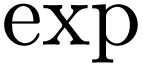 . This is just done by closing
. This is just done by closing 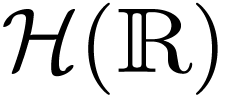 under
under 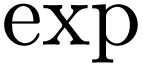 as explained in Lou's lecture. Then embed
as explained in Lou's lecture. Then embed
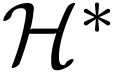 into a model of
into a model of 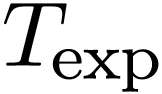 using
Proposition 4, and conclude with Corollary 2.
using
Proposition 4, and conclude with Corollary 2.