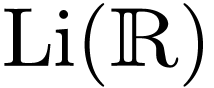 denote the Liouville closure of the field of
constants
denote the Liouville closure of the field of
constants 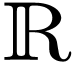 in say transseries.
in say transseries.
|
Let 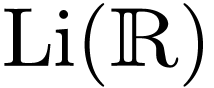 denote the Liouville closure of the field of
constants
denote the Liouville closure of the field of
constants 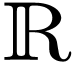 in say transseries.
in say transseries.
Question 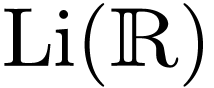 closed under composition?
closed under composition?
Before answering the question in the positive, let me introduce an
equivalent definition of Liouville extensions. Given two Hardy fields
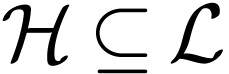 , the extension
, the extension 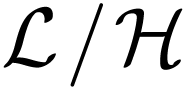 is a Liouville extension if for all
is a Liouville extension if for all 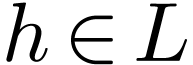 , there are an
, there are an 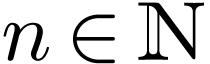 and non-zero
germs
and non-zero
germs 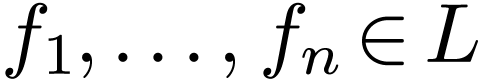 with
with 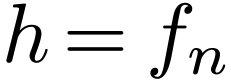 ,
such that for each
,
such that for each 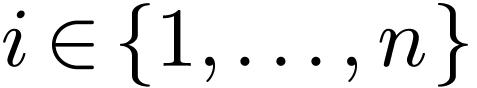 , one of
the following occurs:
, one of
the following occurs:
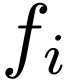 is algeraic over
is algeraic over  ,
,
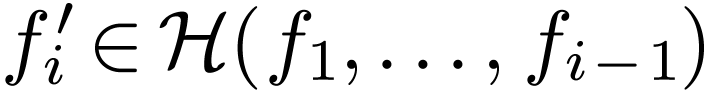 , or
, or
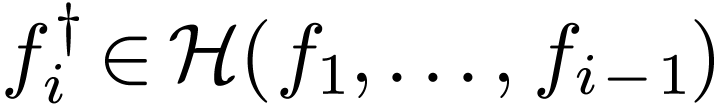 .
.
Given 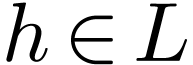 , we define
, we define 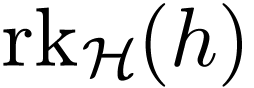 to be the least
to be the least 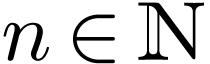 such that such a
decomposition of length
such that such a
decomposition of length 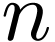 exists. Note that
exists. Note that 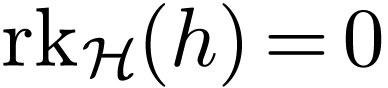 if and only if
if and only if 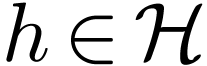 .
Moreover, if
.
Moreover, if 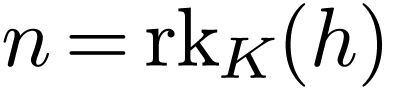 in the situation above, then we
have
in the situation above, then we
have 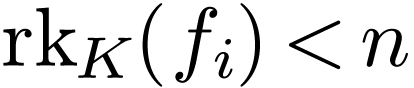 for all
for all  ,
which is why I use this presentaion of Liouville extensions.
,
which is why I use this presentaion of Liouville extensions.
Proposition 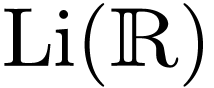 of
of 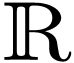 is
closed under composition.
is
closed under composition.
Proof. Let us prove by induction on 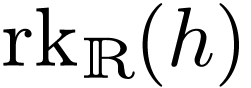 that for all
that for all 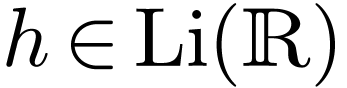 and
and 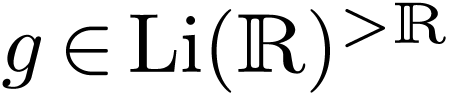 ,
we have
,
we have 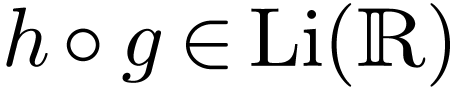 . This is immediate
when
. This is immediate
when 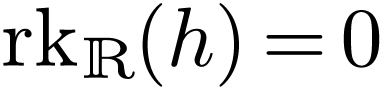 , since then
, since then  is a constant. Let
is a constant. Let  such that the
result holds for germs of rank
such that the
result holds for germs of rank 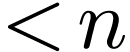 and let
and let 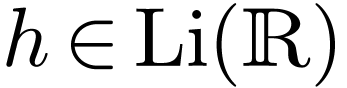 with
with 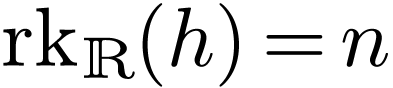 .
.
There are non-zero germs 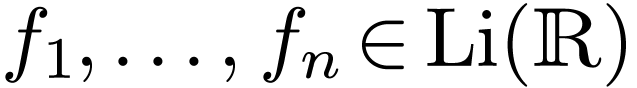 with
with 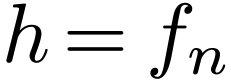 , and where for all
, and where for all 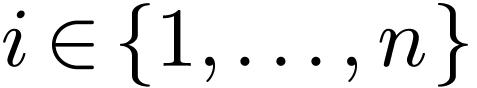 , one of the following occurs:
, one of the following occurs:
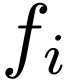 is algeraic over
is algeraic over  ,
,
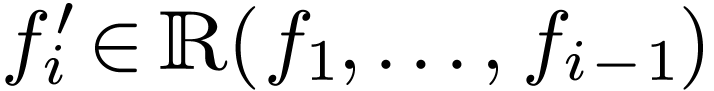 ,
,
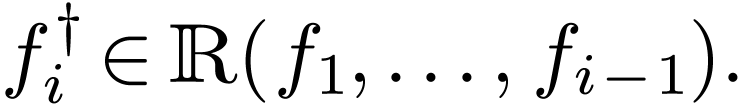
Note that for each  , we have
, we have
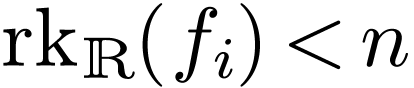 whence
whence 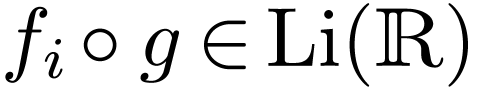 .
We distinguish three cases.
.
We distinguish three cases.
 is algebraic over
is algebraic over 
Then 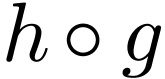 is algebraic over
is algebraic over  , whence algeraic over
, whence algeraic over 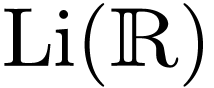 . But
. But 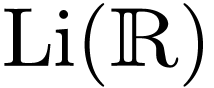 is
real-closed, so
is
real-closed, so 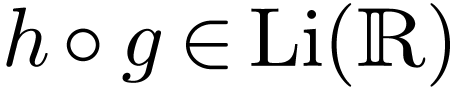 .
.
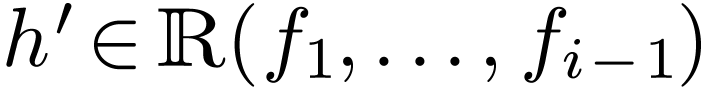
Then
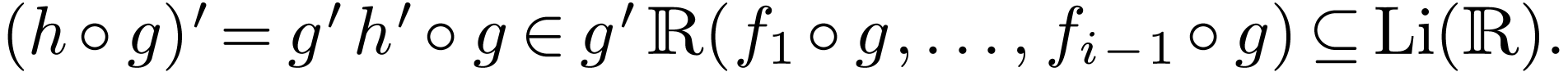
Since 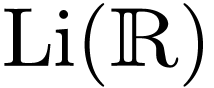 is closed under integration, it
follows that
is closed under integration, it
follows that 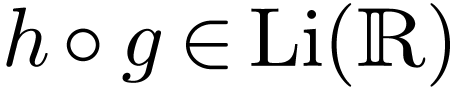 .
.
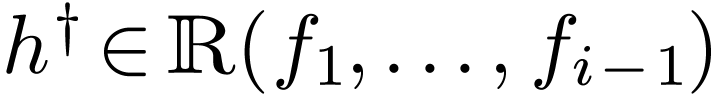
As in the previous case 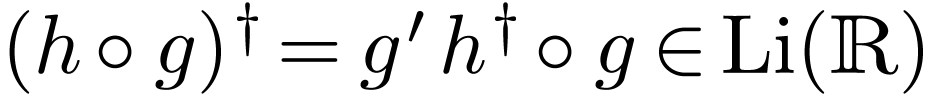 .
We deduce since
.
We deduce since 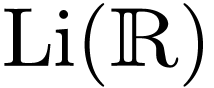 is closed under
exponential integration that
is closed under
exponential integration that 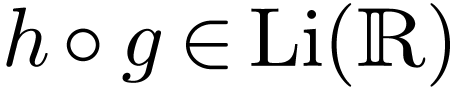 .
.
This concludes the inductive proof.
Remark 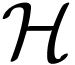 closed under
composition (instead of
closed under
composition (instead of 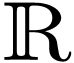 ),
provided that
),
provided that
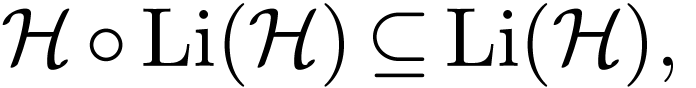
which of course is a problematic inclusion on its own.
Let 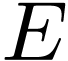 denote Boshernitzan's Hardy field, i.e.
denote Boshernitzan's Hardy field, i.e. 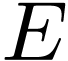 is the intersection of all maximal Hardy fields. In
one of your lectures, I asked you if it was known whether every positive
infinite germ in
is the intersection of all maximal Hardy fields. In
one of your lectures, I asked you if it was known whether every positive
infinite germ in 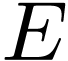 has a level in the sense of
Rosenlicht/Marker-Miller. I.e. given
has a level in the sense of
Rosenlicht/Marker-Miller. I.e. given 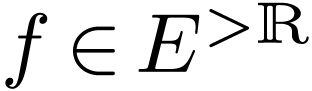 ,
is there an
,
is there an 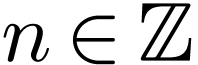 with
with 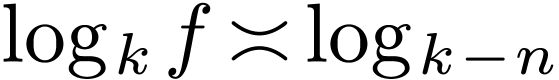 for
sufficiently large
for
sufficiently large 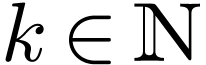 ?
?
Proposition 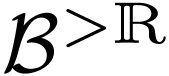 has a level.
has a level.
Proof. This can be deduced from a result of Joris in
his Transserial Hardy fields paper [1]. Consider
the field 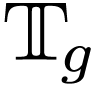 of grid-based transseries. Let
of grid-based transseries. Let 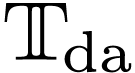 denote the subfield of
denote the subfield of 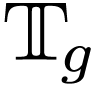 of
transseries. This is an
of
transseries. This is an 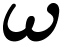 -free,
Newtonian, Liouville-closed H-field with small derivation. By [1,
Theorem 5.12], there is a Hardy field
-free,
Newtonian, Liouville-closed H-field with small derivation. By [1,
Theorem 5.12], there is a Hardy field 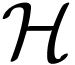 closed
under
closed
under 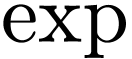 and
and 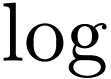 and an
isomorphism
and an
isomorphism
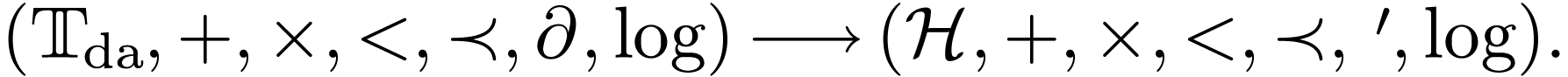
In particular 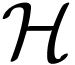 is H-closed. Let
is H-closed. Let 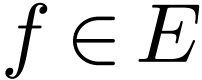 and assume for contradiction that
and assume for contradiction that 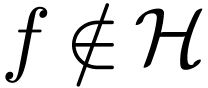 .
Let
.
Let 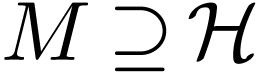 be a maximal Hardy field containing
be a maximal Hardy field containing 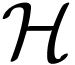 . We have
. We have 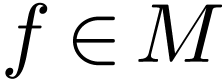 by definition of
by definition of 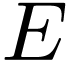 . Now
. Now 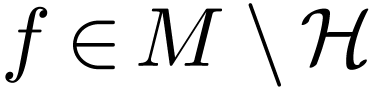 must be
must be 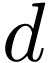 -transcendant
over
-transcendant
over 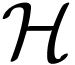 , hence also over
, hence also over 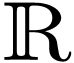 . This contradicts Boshernitzan's
result that each element of
. This contradicts Boshernitzan's
result that each element of 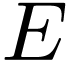 is in fact
d-algebraic. Thus
is in fact
d-algebraic. Thus 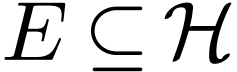 . In
particular, the field
. In
particular, the field 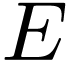 embeds into
embeds into 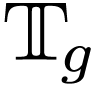 as an ordered exponential field, so each
as an ordered exponential field, so each 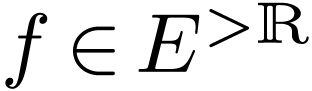 has a level
has a level 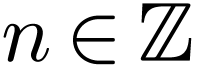 .
.
As far as I know, the only Hardy field with composition which is known not to have levels in this sense is that which is defined in Adele Padgett's forthcoming thesis [2].