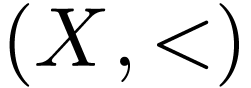 , the binary relation
, the binary relation 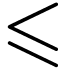 on
on 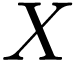 is defined by
is defined by
|
1Ordered domains and fields 1
2Real closure 3
3Cuts and simple extensions 3
3.1The transcendental case 4
3.2The algebraic case 6
4Good cuts and completeness 7
5Cauchy sequences and completeness 8
5.1Cauchy sequences 8
5.2About cofinality 8
5.3Cauchy-completeness 9
6Completion 9
6.1The completion theorem 10
6.2An analogy 11
Bibliography 11
Index 11
Glossary 11
Let us start with some conventions regarding linear (i.e. total) orders.
My orderings are always strict. Given a linear order 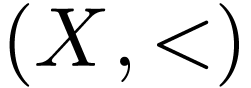 , the binary relation
, the binary relation 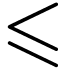 on
on 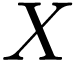 is defined by
is defined by

Given an element 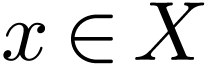 and subsets
and subsets 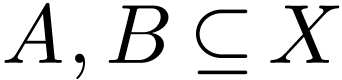 , I write
, I write
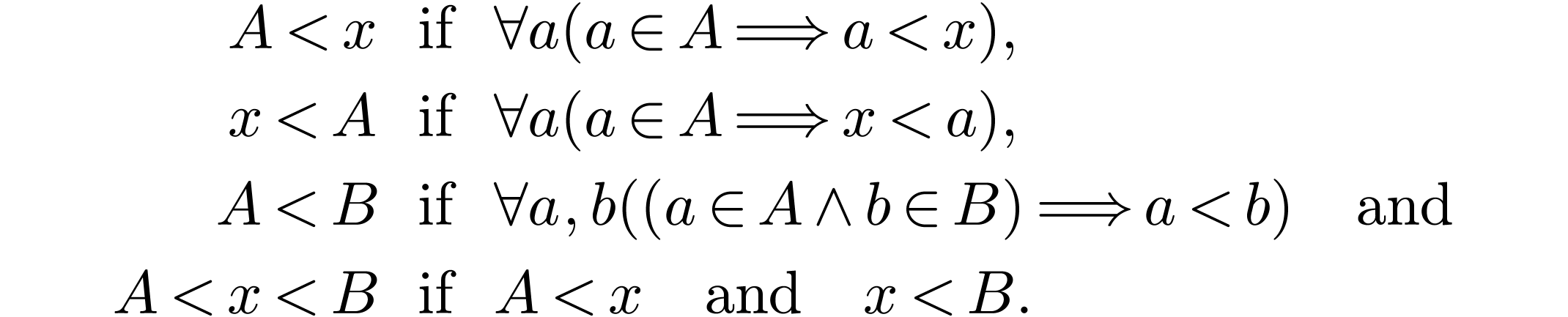
Note that all above statements are vacuously true when 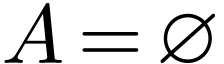 , or
, or 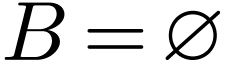 for the two last
ones.
for the two last
ones.
A subset 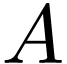 of a linear order
of a linear order 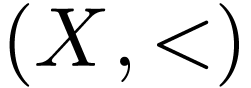 is dense in
is dense in 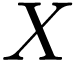 if
if

and that it is cofinal in 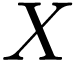 if
it has no strict upper bound in
if
it has no strict upper bound in 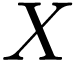 ,
i.e. if
,
i.e. if
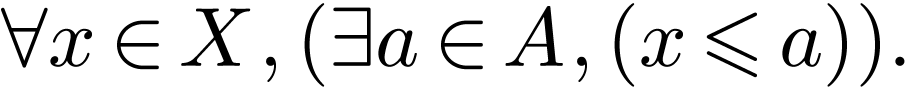
Definition 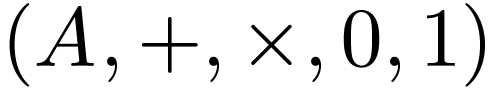 equipped with a linear order
equipped with a linear order  on
on  , with
, with
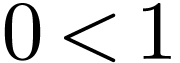 .
.
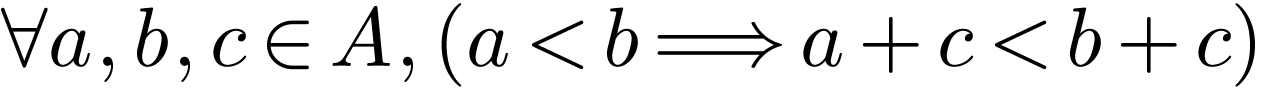 .
.
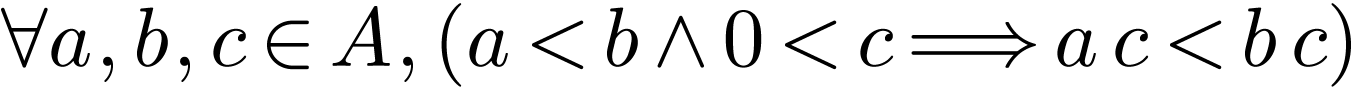 .
.
An ordered field is an ordered domain which is a field.
Definition 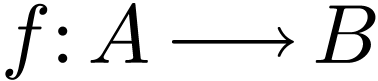 is said cofinal if
is said cofinal if 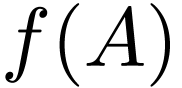 is cofinal in
is cofinal in 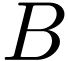 ,
dense if
,
dense if 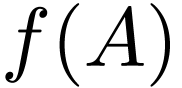 is dense in
is dense in
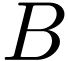 (as a linear order).
(as a linear order).
If 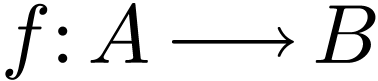 is a (cofinal, dense) embedding, then I
say that
is a (cofinal, dense) embedding, then I
say that 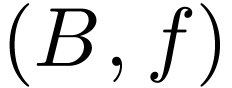 is a (cofinal, dense)
extension of
is a (cofinal, dense)
extension of 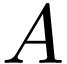 .
.
Given an ordered domain  , I
write
, I
write
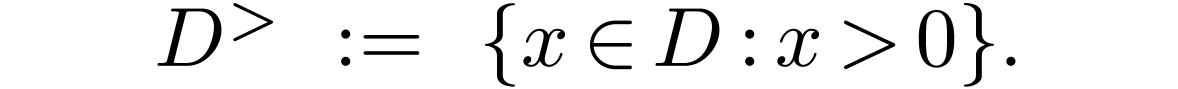
Moreover, for all 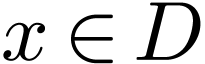 , I write
, I write
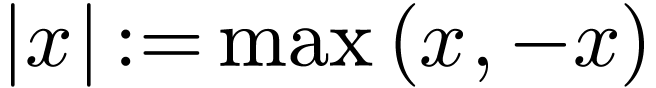 for the absolute value
of
for the absolute value
of 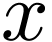 .
.
Definition 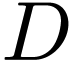 is a domain, then a positive
cone on
is a domain, then a positive
cone on 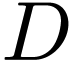 is a subset
is a subset
 of
of 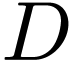 such that for all
such that for all
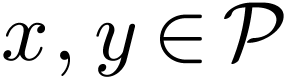 , we have
, we have
Note that if 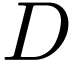 is an ordered domain, then
is an ordered domain, then 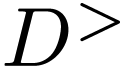 is a positive cone on
is a positive cone on 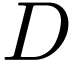 .
We have the following converse.
.
We have the following converse.
Lemma  is a positive cone on
is a positive cone on 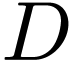 , then
the relation
, then
the relation 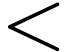 defined on
defined on  by
by
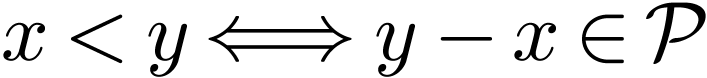
is an order on  , and
, and  is an ordered domain with
is an ordered domain with 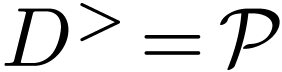 .
.
Sketch of Proof. The anti-reflexivity of  follows from Definition 1.3(c),
its transitivity follows from Definition 1.3(a),
its linearity follows from Definition 1.3(e),
follows from Definition 1.3(c),
its transitivity follows from Definition 1.3(a),
its linearity follows from Definition 1.3(e),
 follows from Definition 1.3(d) and the compatibilities between
follows from Definition 1.3(d) and the compatibilities between  and
and
 and
and  follow from
Definition 1.3(a) and Definition 1.3(b) respectively.
follow from
Definition 1.3(a) and Definition 1.3(b) respectively.
Proposition 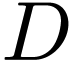 be an ordered domain. There is a unique ordering of its
fraction field
be an ordered domain. There is a unique ordering of its
fraction field 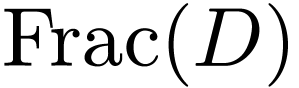 such that
such that 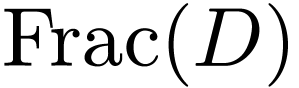 is an extension of
is an extension of 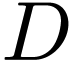 .
.
Sketch of Proof. We define a positive cone  on
on 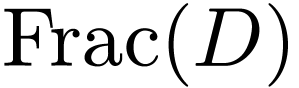 as follows:
as follows:
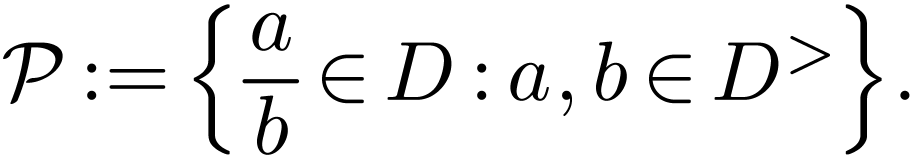
We immediately have  and
and  , as well as Definition 1.3(e)
and Definition 1.3(b). For
, as well as Definition 1.3(e)
and Definition 1.3(b). For 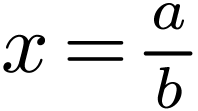 and
and 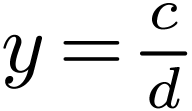 in
in  ,
where
,
where 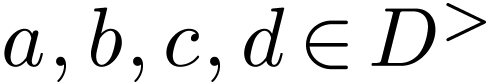 , we have
, we have 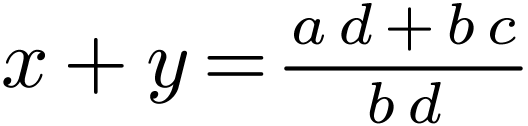 where
where 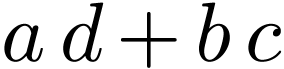 and
and 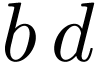 are strictly positive, whence
are strictly positive, whence  .
So
.
So  is a positive cone. Since
is a positive cone. Since  contains
contains  (as naturally embedded into
(as naturally embedded into 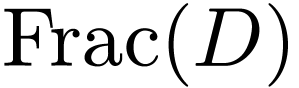 ), the corresponding ordered domain
is an extension of
), the corresponding ordered domain
is an extension of 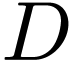 .
.
Now if  is an order on
is an order on 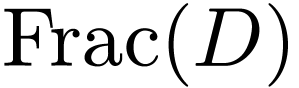 such that
such that 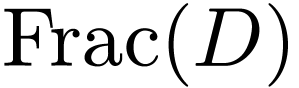 is an ordered ring extension of
is an ordered ring extension of 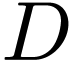 , then
, then 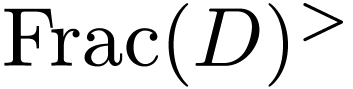 contains
contains 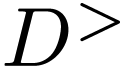 , whence
, whence  by Definition 1.3(b). We deduce
that
by Definition 1.3(b). We deduce
that  is the order derived from
is the order derived from  .
.
So in the sequel, I will extend orderings to fraction fields without
mention. The fraction field operation 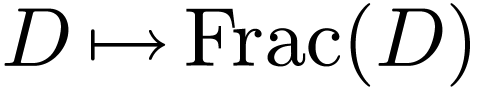 induces a
functor from the category of ordered domains with embeddings, to the
gategory of ordered fields with embeddings, by sending an embedding
induces a
functor from the category of ordered domains with embeddings, to the
gategory of ordered fields with embeddings, by sending an embedding 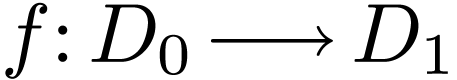 to the well-defined map
to the well-defined map  .
This functor is left adjoint to the forgetfull functor.
.
This functor is left adjoint to the forgetfull functor.
Remark 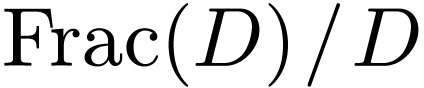 might not be cofinal. For instance,
consider the ordered domain
might not be cofinal. For instance,
consider the ordered domain 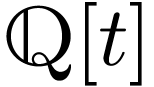 whose positive cone
is the set of polynomials with strictly positive leading coefficient.
Now consider the ordered domain
whose positive cone
is the set of polynomials with strictly positive leading coefficient.
Now consider the ordered domain 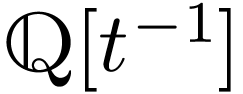 contained in
contained in
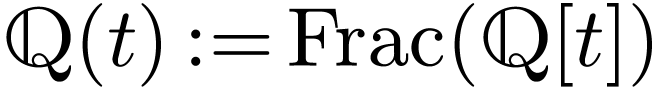 . We have
. We have 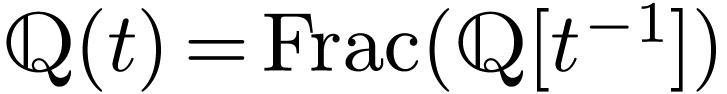 but the element
but the element  satisfies
satisfies 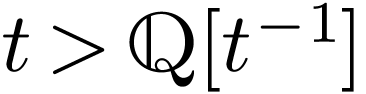 .
.
I will say that an extension of ordered fields is algebraic if it is algebraic as a field extension.
Lemma
Sketch of Proof. Let 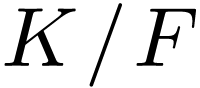 be an
algebraic extension of ordered fields. We will prove by induction on
be an
algebraic extension of ordered fields. We will prove by induction on
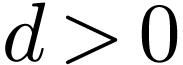 that for all
that for all 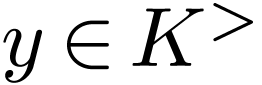 ,
if there is a polynomial
,
if there is a polynomial 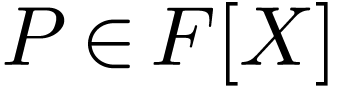 of degree
of degree 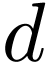 with
with 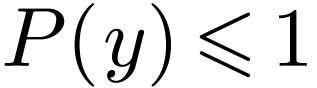 , then
, then
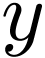 has an upper bound in
has an upper bound in  .
.
This is immediate if 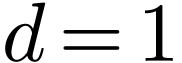 . Let
. Let
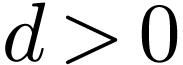 such that the result holds at
such that the result holds at 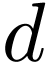 , and let
, and let 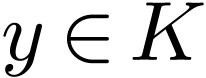 and
and 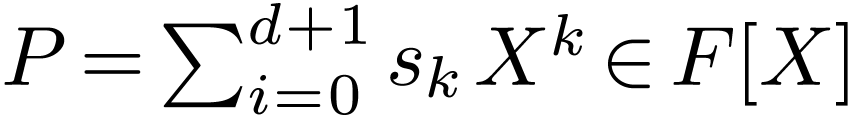 with
with 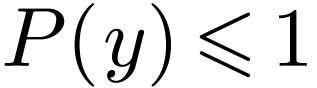 and
and 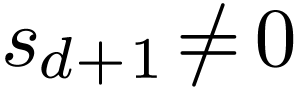 . Set
. Set 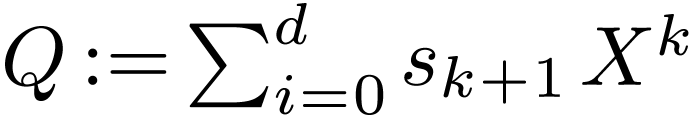 ,
so that
,
so that
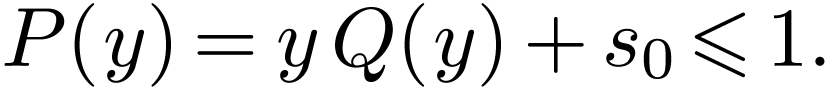
We have 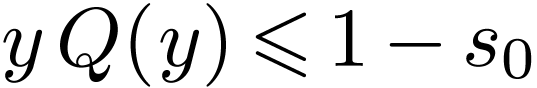 . If
. If 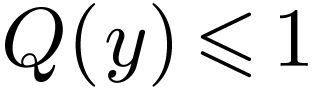 , then we conclude by our induction hypothesis
that
, then we conclude by our induction hypothesis
that 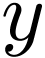 has an upper bound in
has an upper bound in  . If
. If 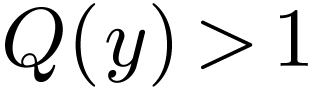 ,
then we deduce that
,
then we deduce that 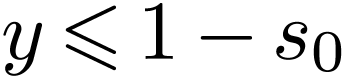 , so
, so 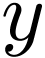 has an upper bound in
has an upper bound in  .
.
By induction, the result holds in general. Now since 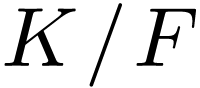 is algebraic, for all
is algebraic, for all 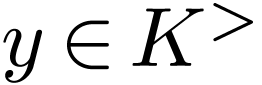 , there
is a
, there
is a 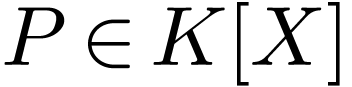 with degree
with degree 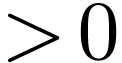 and
and
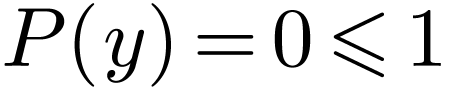 , so any such
, so any such 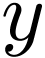 has an upper bound in
has an upper bound in  .
We deduce that
.
We deduce that 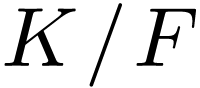 is cofinal.
is cofinal.
Definition
By a famous result of Artin and Schreier, real-closed fields are exactly
the fields 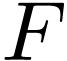 whose absolute Galois group has
finite order (i.e. with
whose absolute Galois group has
finite order (i.e. with 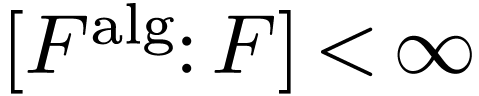 ),
or, equivalently, order
),
or, equivalently, order 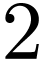 .
They are ordered according to the positive cone
.
They are ordered according to the positive cone 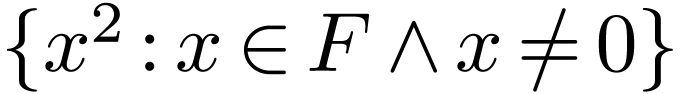 .
.
We have the following famous theorem of Tarski:
Tarski's theorem. An ordered field is real-closed if and only if it has the same first order properties as the ordered field of real numbers.
This means that in real-closed fields, elementary statements regarding
polynomials or more complicated definable functions and sets which are
satisfied in 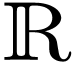 , are valid. We
will use this in the next section. Moreover, again by Artin-Schreier, we
have a real closure functor:
, are valid. We
will use this in the next section. Moreover, again by Artin-Schreier, we
have a real closure functor:
Theorem  , there is an algebraic
extension
, there is an algebraic
extension 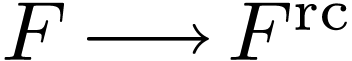 where
where 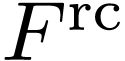 is real-closed. If
is real-closed. If 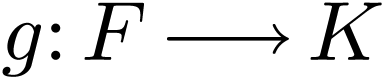 is an extension and
is an extension and 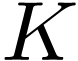 is real-closed, then there is a unique
is real-closed, then there is a unique 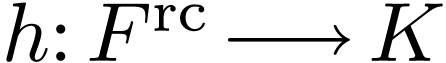 with
with 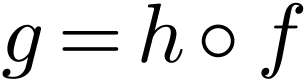 .
.
The extension 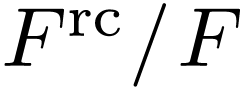 is called the real
closure of
is called the real
closure of 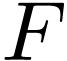 .
By the above initial property, it is unique up to unique isomorphism, so
we consider that
.
By the above initial property, it is unique up to unique isomorphism, so
we consider that 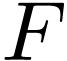 is naturally contained in
is naturally contained in 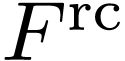 .
.
In this section, we construct simple extensions of ordered fields. The method is inspired from Kaplansky's work in his paper Maximal fields with valuation II [3], except I use cuts instead of pseudo-Cauchy sequences. I will use the following definition of cuts:
Definition  is an ordered pair
is an ordered pair 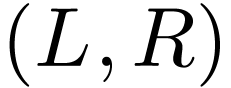 where
where 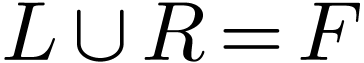 ,
, 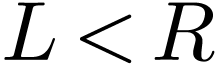 and
and 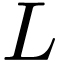 has no maximum. We say that the cut
has no maximum. We say that the cut 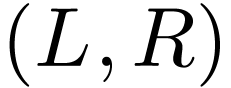 is filled if
is filled if 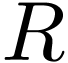 has a minimum, unfilled otherwise.
has a minimum, unfilled otherwise.
Lemma 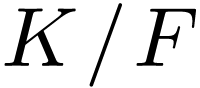 be a cofinal proper extension of ordered fields. For
all
be a cofinal proper extension of ordered fields. For
all 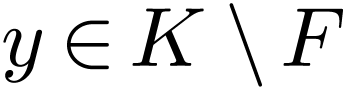 , the pair
, the pair 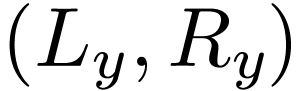 where
where
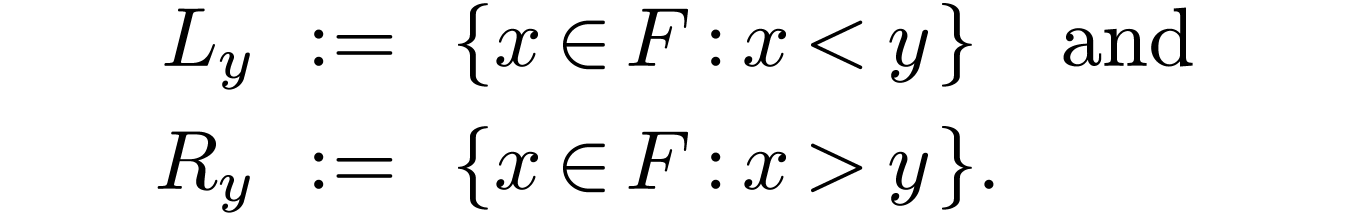
is an unfilled cut over  .
.
Sketch of Proof. We have 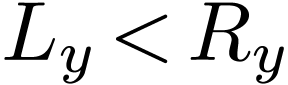 by
definition. Since
by
definition. Since 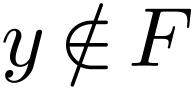 , Any
, Any 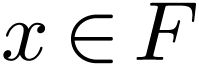 must satisfy
must satisfy 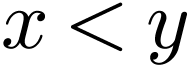 or
or 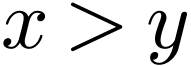 , whence
, whence 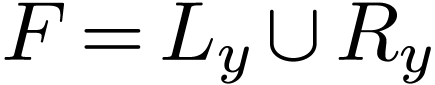 .
Now for
.
Now for 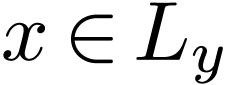 , there is an
, there is an 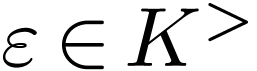 with
with  . But
. But
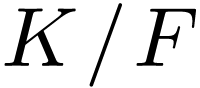 is cofinal, so there is a
is cofinal, so there is a 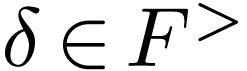 with
with 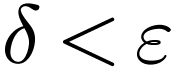 , whence
, whence 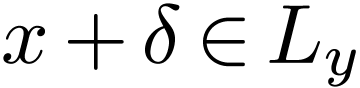 which shows that
which shows that 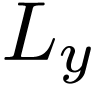 has no maximum.
Likewise
has no maximum.
Likewise 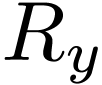 has no minimum, so
has no minimum, so 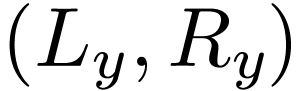 is an unfilled cut.
is an unfilled cut.
In what follows, we will see how to construct simple cofinal ordered
field extensions using unfilled cuts. We start with important remarks on
the sign of polynomials near unfilled cuts. Let 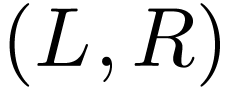 be an unfilled cut in
be an unfilled cut in  .
If
.
If 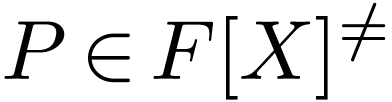 is a non-zero polynomial, then
is a non-zero polynomial, then 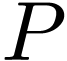 has finitely many roots in the real closure
has finitely many roots in the real closure 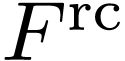 of
of 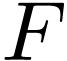 . Since
. Since 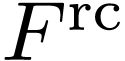 is real-closed, Tarski's theorem implies that it has
the same first-order properties as
is real-closed, Tarski's theorem implies that it has
the same first-order properties as 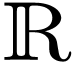 .
In particular
.
In particular 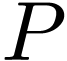 satisfies the intermediate value
theorem on
satisfies the intermediate value
theorem on 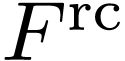 . So
. So 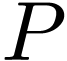 has constant sign between roots in
has constant sign between roots in 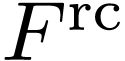 (since between any sign shift there ought to be a root by the IVT).
Assume that
(since between any sign shift there ought to be a root by the IVT).
Assume that 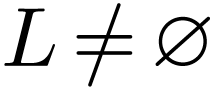 . Then since
. Then since 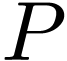 has finitely many roots in
has finitely many roots in 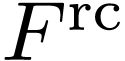 and
and  has no maximum, there is a final segment of
has no maximum, there is a final segment of
 (in
(in  )
where
)
where 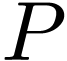 has constant sign
has constant sign  . Likewise, if
. Likewise, if  ,
since
,
since  has no minimum, there is an initial
segment of
has no minimum, there is an initial
segment of 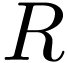 where
where 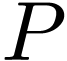 has
constant sign
has
constant sign 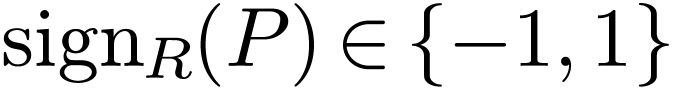 . I will leave
. I will leave
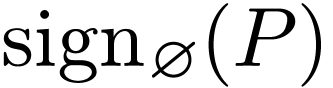 undefined.
undefined.
We say that 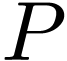 is an annihilator
polynomial of
is an annihilator
polynomial of 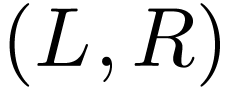 if
if 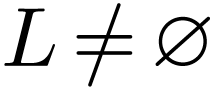 and
and 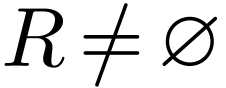 and
and 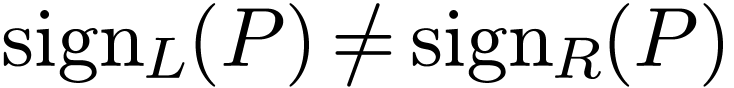 . Annihilator polynomials of
. Annihilator polynomials of 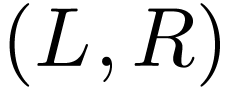 of minimal degree are called minimal polynomials of
of minimal degree are called minimal polynomials of
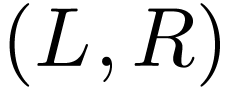 .
.
Remark  where
where 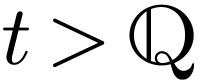 , the cut
, the cut 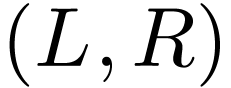 where
where 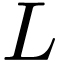 is the set of finite fractions and
is the set of finite fractions and 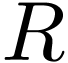 is the set of positive infinite fractions. Then
is the set of positive infinite fractions. Then 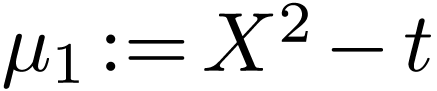 and
and 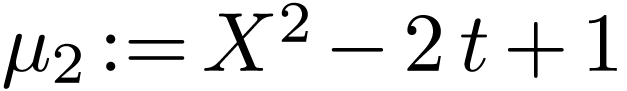 are both minimal polynomials of
are both minimal polynomials of  .
.
In this subsection, we assume that  has no
annihilator polynomial. Then for
has no
annihilator polynomial. Then for 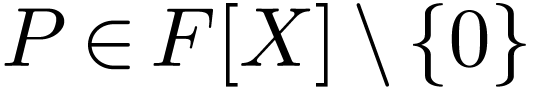 ,
we define
,
we define 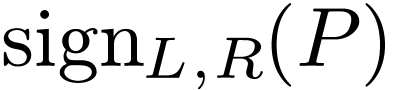 as
as 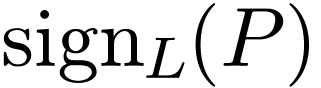 if
if  is non-empty, and as
is non-empty, and as 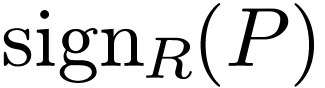 if
if 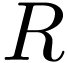 is non-empty. Note that this is well-defined. We also
set
is non-empty. Note that this is well-defined. We also
set 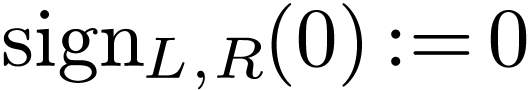 .
.
For 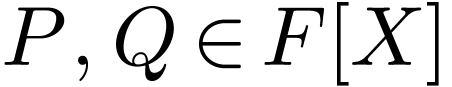 with
with 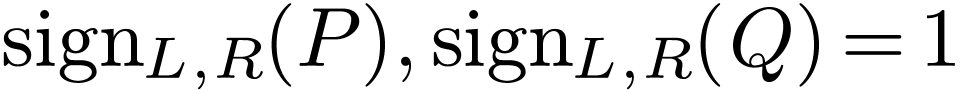 ,
we have
,
we have 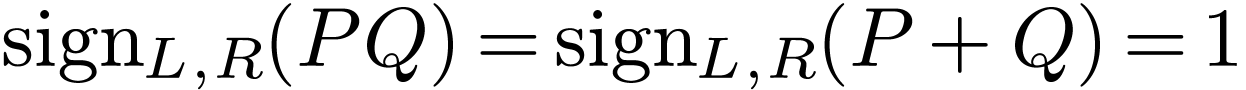 . It is easy to see
consequently that the set of polynomials
. It is easy to see
consequently that the set of polynomials 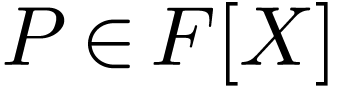 with
with
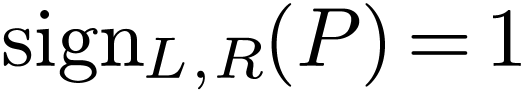 is a positive cone on
is a positive cone on 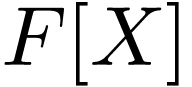 . We write
. We write 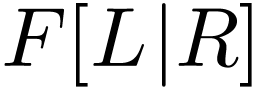 for the
corresponding ordered domain, and
for the
corresponding ordered domain, and 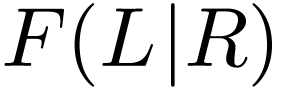 for
its fraction field, which is thus a field extension of
for
its fraction field, which is thus a field extension of 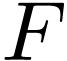 .
.
Proposition 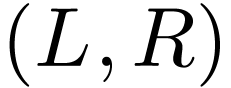 has no annihilator polynomial,
then
has no annihilator polynomial,
then 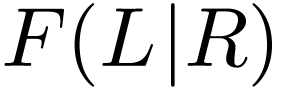 is an ordered field extension of
is an ordered field extension of  where
where  .
.
Sketch of Proof. It is easy to see that 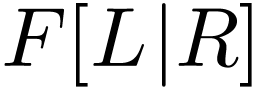 is an ordered domain extension of
is an ordered domain extension of  , since the sign
, since the sign 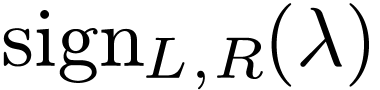 of any
constant polynomial
of any
constant polynomial  is that of the constant
is that of the constant  in
in  . So
. So
 is an ordered field extension of
is an ordered field extension of  . Now for
. Now for 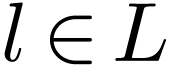 and
and 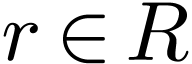 , we have
, we have 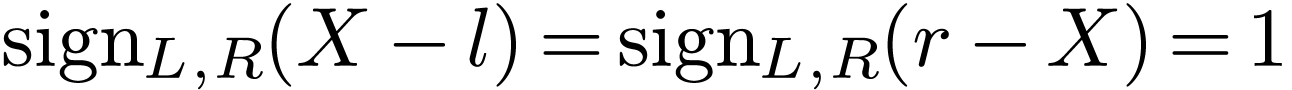 . We deduce that
. We deduce that 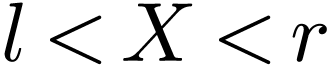 .
.
Lemma 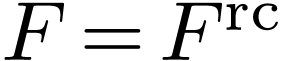 be real-closed. Let
be real-closed. Let 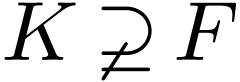 be a
proper extension, let
be a
proper extension, let 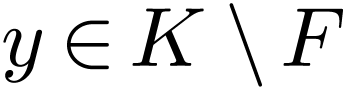 .
Set
.
Set
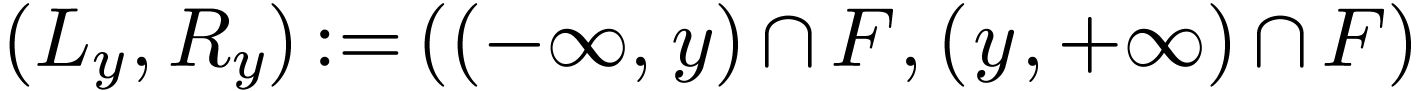
and assume that 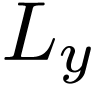 has no maximum and
has no maximum and 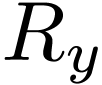 has no minimum. Then
has no minimum. Then 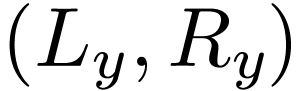 is an
unfilled cut over
is an
unfilled cut over  and it has no annihilator
polynomial.
and it has no annihilator
polynomial.
Sketch of Proof. That 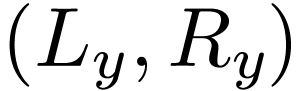 is an
unfilled cut over
is an
unfilled cut over  is immediate by definition.
Assume for contradiction that
is immediate by definition.
Assume for contradiction that 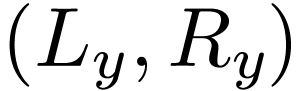 has an annihilator
polynomial
has an annihilator
polynomial  over
over  .
In particular, neither
.
In particular, neither 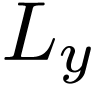 nor
nor 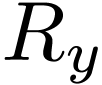 are empty. Since
are empty. Since  is real-closed, all roots of
is real-closed, all roots of
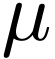 in
in 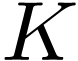 lie in
lie in  , so there are an
, so there are an 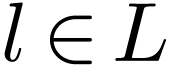 and
an
and
an 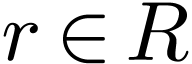 such that
such that 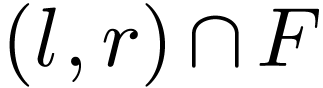 contains no
root of
contains no
root of 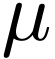 and with
and with 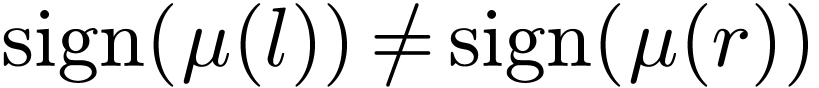 .
But then by the IVT for
.
But then by the IVT for 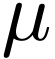 in
in  we have a root of
we have a root of 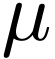 in
in 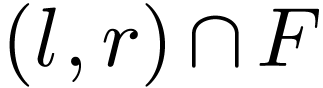 : a contradiction.
: a contradiction.
Theorem 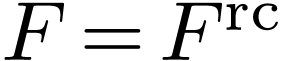 be real-closed. Let
be real-closed. Let 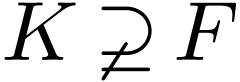 be a proper
extension let
be a proper
extension let 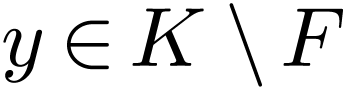 . Set
. Set
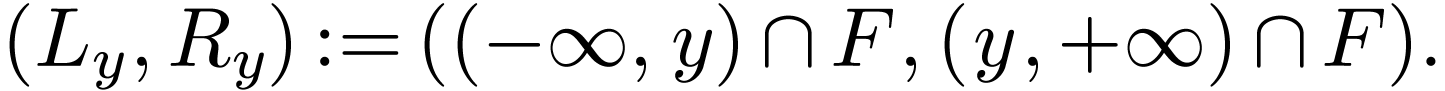
Assume that 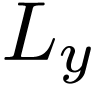 has no maximum and
has no maximum and 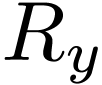 has no minimum. Then there is a unique ordered field
embedding
has no minimum. Then there is a unique ordered field
embedding 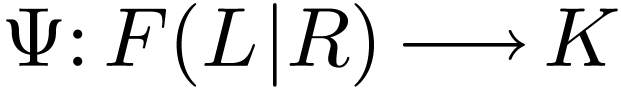 over
over  with
with
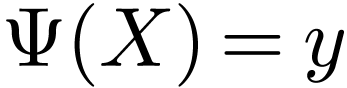 .
.
Sketch of Proof. Since  is
real-closed, the extension
is
real-closed, the extension 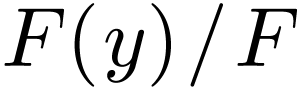 is transcendental,
and
is transcendental,
and 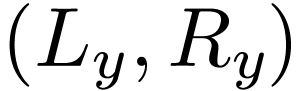 has no annihilator polynomial by Lemma 3.5. So there is a field isomorphism
has no annihilator polynomial by Lemma 3.5. So there is a field isomorphism
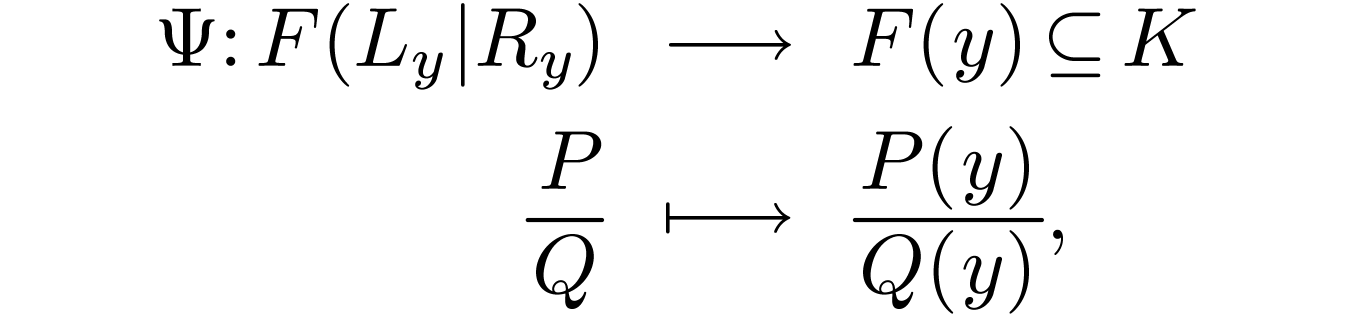
which is the unique ring morphism 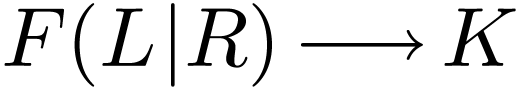 over
over  which sends
which sends 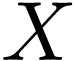 to
to 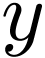 . Let us show that
. Let us show that 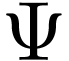 is
strictly increasing. It is enough to show that for
is
strictly increasing. It is enough to show that for 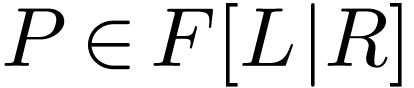 with
with 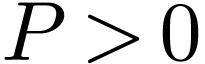 , we have
, we have 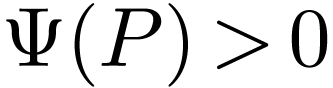 . Now, for such
. Now, for such 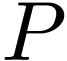 ,
there are
,
there are 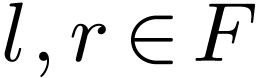 with
with 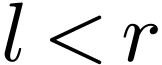 such that
we have
such that
we have 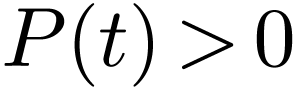 for all
for all 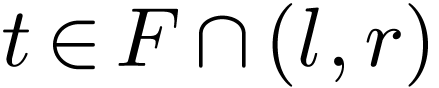 .
So
.
So 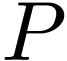 has no zero in
has no zero in 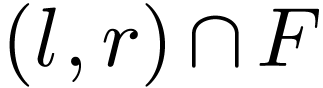 .
But
.
But  is real-closed, so
is real-closed, so 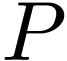 has no zero in
has no zero in 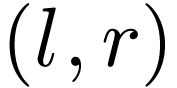 and must have constant, strictly
positive sign on this set. In particular, we get
and must have constant, strictly
positive sign on this set. In particular, we get 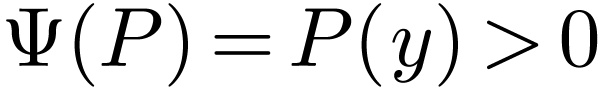 since
since 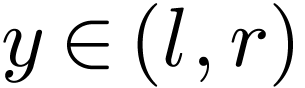 . So
. So 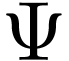 is strictly increasing.
is strictly increasing.
Theorem 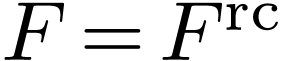 be real-closed. Let
be real-closed. Let  be a proper
extension let
be a proper
extension let 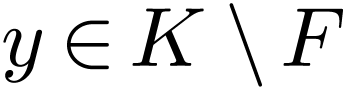 . Set
. Set
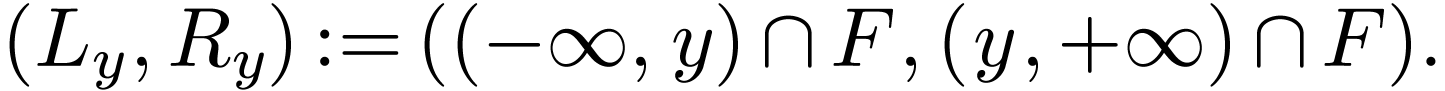
If 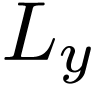 has a maximum
has a maximum 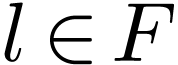 , then there is a unique ordered field embedding
, then there is a unique ordered field embedding
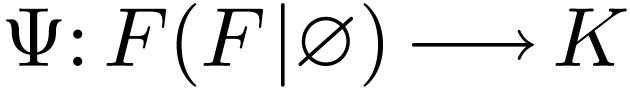 over
over  with
with 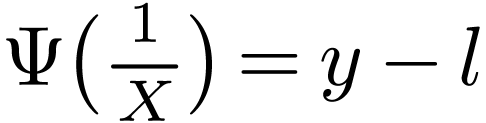 . If
. If 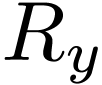 has a minimum
has a minimum
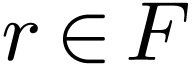 , then there is a unique
ordered field embedding
, then there is a unique
ordered field embedding 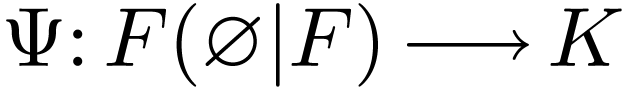 over
over  with
with 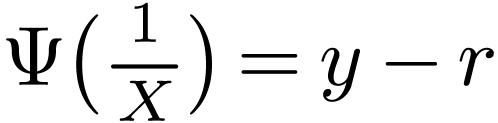 .
.
Sketch of Proof. Again the fields embeddings are
well-defined and unique, so there remains only to show that they are
strictly increasing, hence that they preserve the sign of elements in
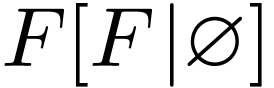 and
and 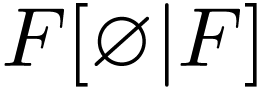 respectively.
respectively.
We treat the first case. Let 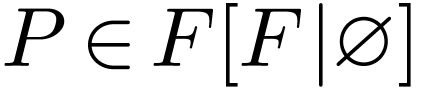 be strictly
positive. So
be strictly
positive. So 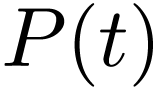 is strictly positive for large
enough
is strictly positive for large
enough 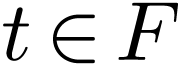 . So there is an
. So there is an 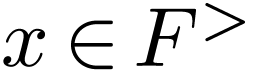 with
with 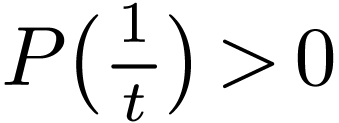 for all
for all 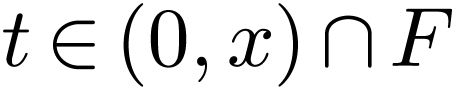 . Since
. Since  is real-closed,
as in the previous proof, we must have
is real-closed,
as in the previous proof, we must have 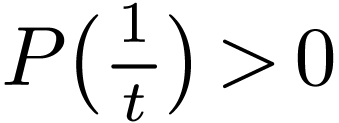 for all
for all
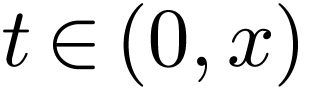 in
in 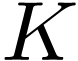 as well, whence
as well, whence 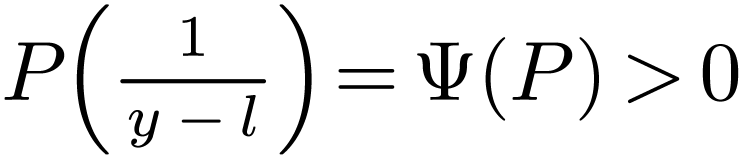 . This concludes the proof. The
case when
. This concludes the proof. The
case when 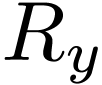 has a minimum is symmetric.
has a minimum is symmetric.
So we have a characterization of orderings on simple extensions of
real-closed fields via cuts and sets of the form 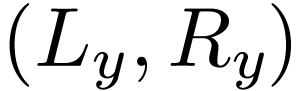 where
where 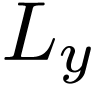 has a maximum or
has a maximum or 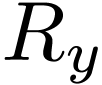 has a minimum. One final question is: when is the extension
has a minimum. One final question is: when is the extension 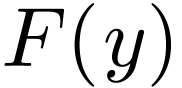 cofinal? Using the chracterizations of orderings using
cuts, this reduces to the following:
cofinal? Using the chracterizations of orderings using
cuts, this reduces to the following:
Lemma 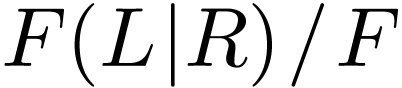 is cofinal if and only if
is cofinal if and only if 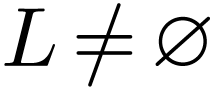 and
and 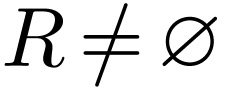 .
.
Sketch of Proof. If 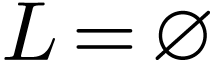 ,
then
,
then 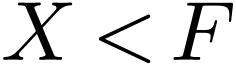 in
in 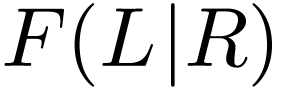 by definition,
so the extension is not cofinal. Likewise
by definition,
so the extension is not cofinal. Likewise 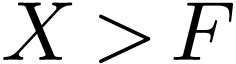 in
in
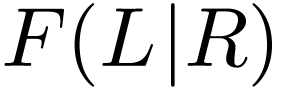 if
if 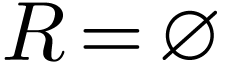 .
Conversely, assume that
.
Conversely, assume that 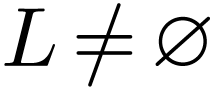 and that
and that 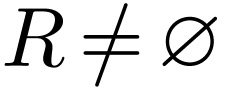 . So we have
. So we have 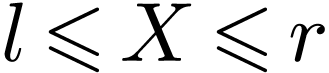 for a
certain
for a
certain  . It follows that for
all
. It follows that for
all  , there is an
, there is an
with 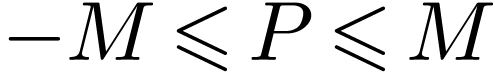 in
in 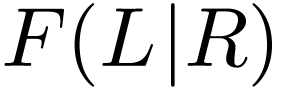 .
Now let
.
Now let 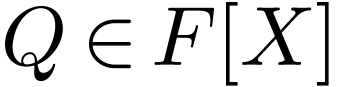 be positive. Our goal will be to prove
that there are a
be positive. Our goal will be to prove
that there are a 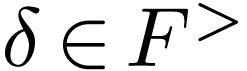 and an
and an 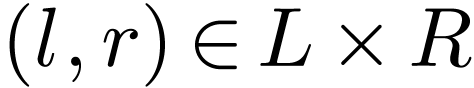 with
with 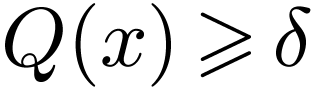 for all
for all 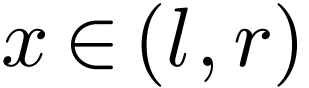 ,
which would mean that
,
which would mean that 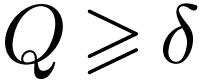 in
in 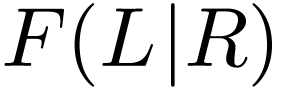 .
.
Assume for contradiction that for all 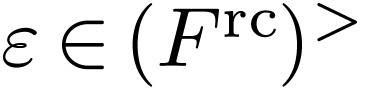 ,
there is an
,
there is an 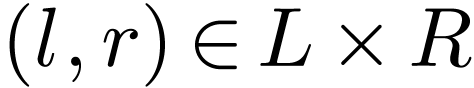 , such that
, such that 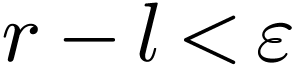 and that the interval
and that the interval 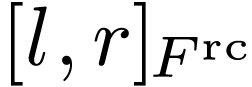 in
in 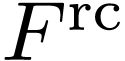 contains a root of
contains a root of  .
Choosing
.
Choosing  smaller than the distances between
distinct roots of
smaller than the distances between
distinct roots of  , we may
fix
, we may
fix 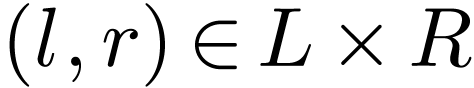 and
and 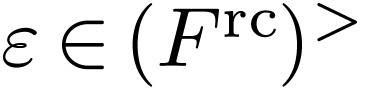 such that
such that 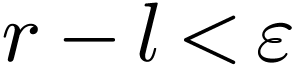 and that
and that 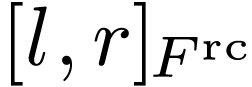 contains a unique
root
contains a unique
root 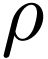 of
of  .
Let
.
Let 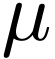 denote the minimal polynomial of
denote the minimal polynomial of 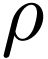 over
over  . Recall
that
. Recall
that  is a perfect field since it has
characteristic zero. So
is a perfect field since it has
characteristic zero. So 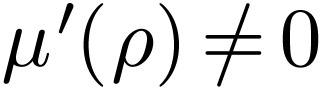 ,
which implies by Tarski's theorem that the function
,
which implies by Tarski's theorem that the function 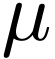 takes opposite signs on small intervals
takes opposite signs on small intervals 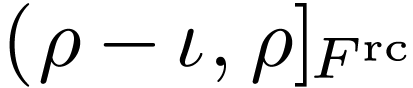 and
and  for small enough
for small enough 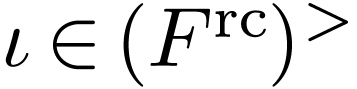 .
Our assumption implies that there is an
.
Our assumption implies that there is an 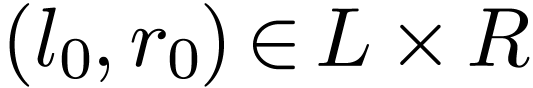 such
that
such
that 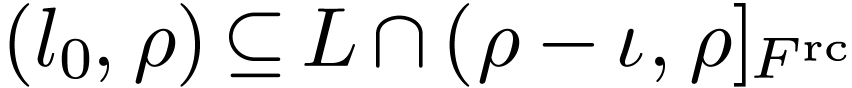 and
and  .
But then we have
.
But then we have 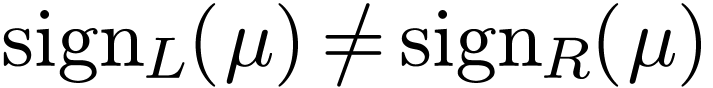 , so
, so 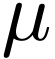 is an annihilator polynomial of
is an annihilator polynomial of 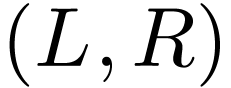 : a contradiction. We deduce that one of the
following holds:
: a contradiction. We deduce that one of the
following holds:
There is an 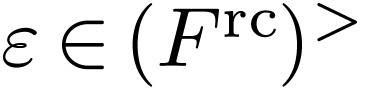 such that
such that 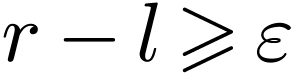 for all
for all 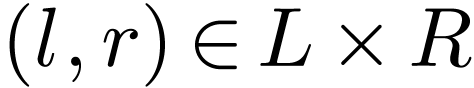 . In that case,
by Lemma 2.1, we may assume that
. In that case,
by Lemma 2.1, we may assume that 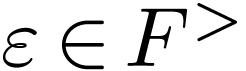 . By Tarski's theorem, given
. By Tarski's theorem, given 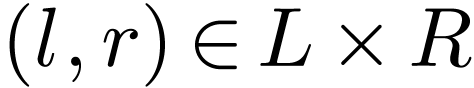 , the polynomial function
, the polynomial function  takes a strictly positive minimal value
takes a strictly positive minimal value  on
the set
on
the set
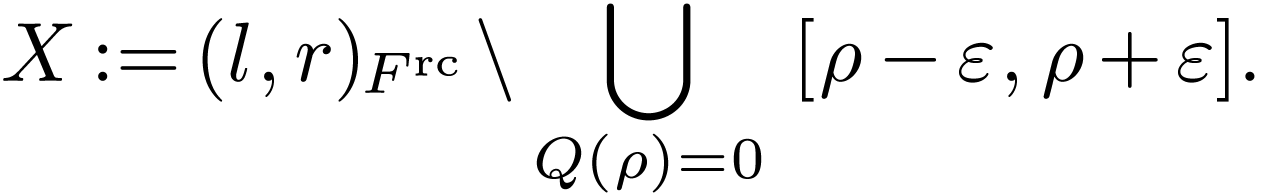
But by our assumption, we may choose 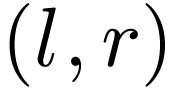 so that
so that
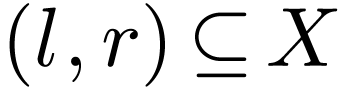 , whence
, whence 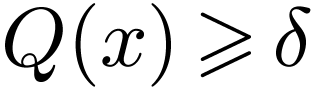 for all
for all 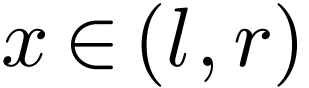 .
.
There is an 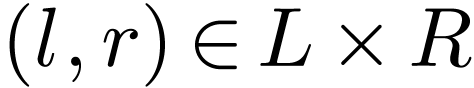 such that
such that 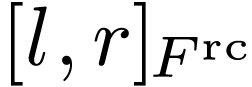 contains no root of
contains no root of  . In
that case, the polynomial function
. In
that case, the polynomial function  takes a
strictly positive minimal value
takes a
strictly positive minimal value 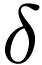 (in
(in 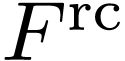 ) on
) on 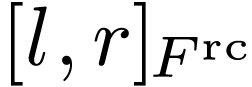 , whence
, whence 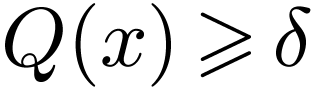 for all
for all 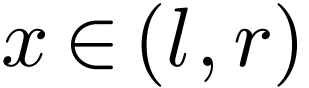 .
.
Now for 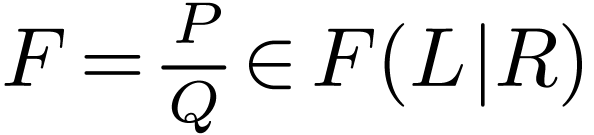 where
where 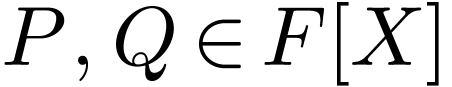 ,
we may choose
,
we may choose 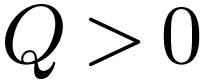 and thus obtain a
and thus obtain a 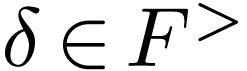 with
with 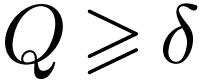 and an
and an  with
with 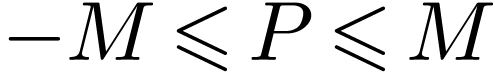 , whence
, whence 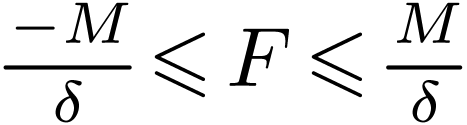 . This shows that
. This shows that 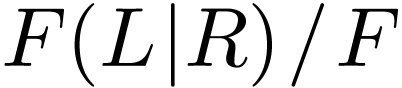 is
cofinal.
is
cofinal.
In this subsection, we assume that 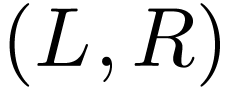 has an
annihilator polynomial. In particular,
has an
annihilator polynomial. In particular, 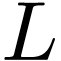 and
and
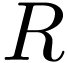 are non-empty. Pick a minimal polynomial
are non-empty. Pick a minimal polynomial 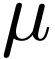 of
of 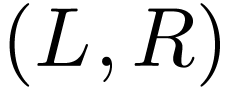 .
.
Claim: 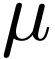 is irreducible in
is irreducible in 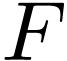 . Indeed, for strictly lower degree
polynomials
. Indeed, for strictly lower degree
polynomials 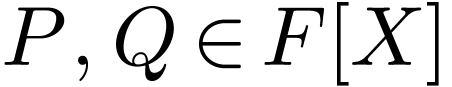 , we have
, we have 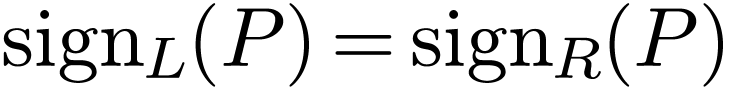 and
and 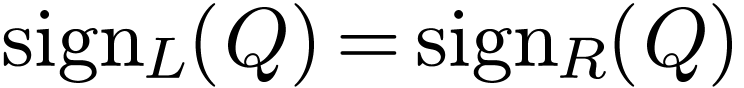 by minimality, whence
by minimality, whence
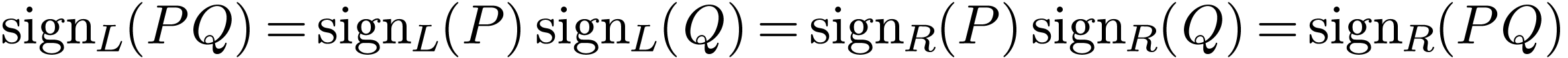 .
.
So the quotient ring 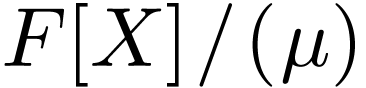 is a field extension of
is a field extension of
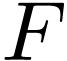 . We define a positive cone
for
. We define a positive cone
for 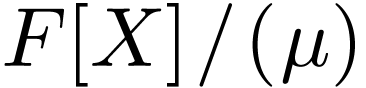 as follows. Given
as follows. Given  , the Euclidean division of
, the Euclidean division of 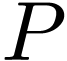 by
by 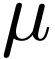 yields a unique
yields a unique 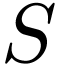 with
with
 and
and
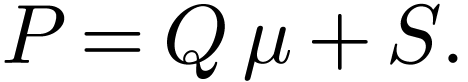
By minimality of 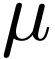 , we may set
, we may set
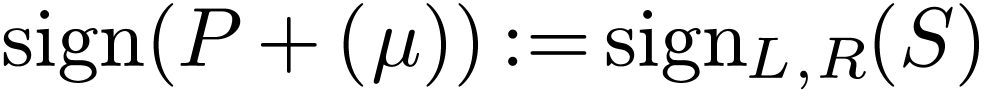 and define
and define  as the set of
elements
as the set of
elements 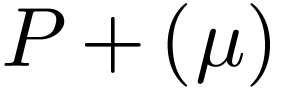 with
with 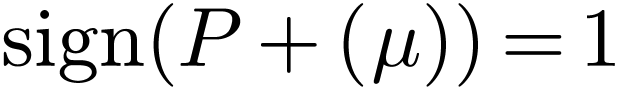 .
Note that Definition 1.3(c,d,e) are satisfied. Consider
.
Note that Definition 1.3(c,d,e) are satisfied. Consider 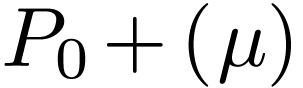 and
and 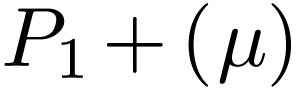 in
in 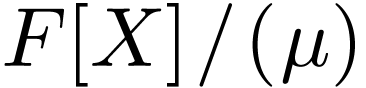 with positive sign. We
readily see that
with positive sign. We
readily see that 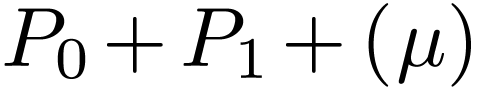 has positive sign, so
has positive sign, so  satisfies Definition 1.3(a).
satisfies Definition 1.3(a).
We next deal with Definition 1.3(b). Write
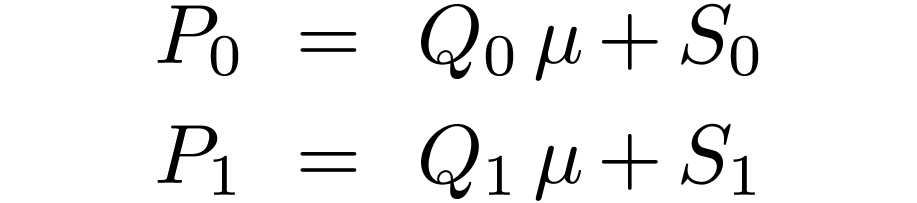
as above, and also consider the Euclidean division of 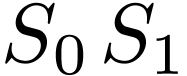 by
by 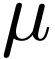 :
:
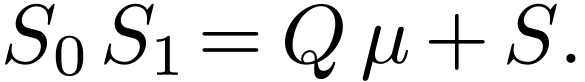
Since 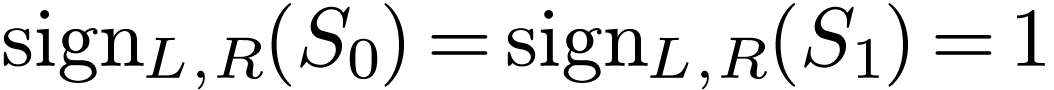 , we have
, we have 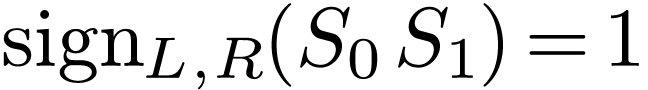 . Assume for contradiction that
. Assume for contradiction that 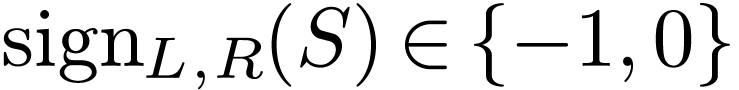 . So
. So  is negative for
large enough
is negative for
large enough 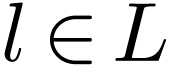 and
and 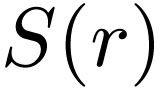 is
negative for small enough
is
negative for small enough 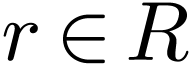 .
In particular
.
In particular 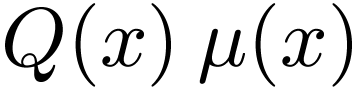 is strictly negative for large
enough
is strictly negative for large
enough 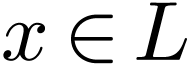 and small enough
and small enough 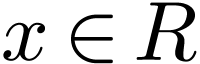 . Since
. Since 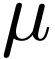 is an anihilator
polynomial of
is an anihilator
polynomial of 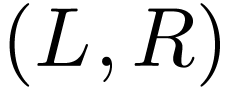 , this implies
that
, this implies
that 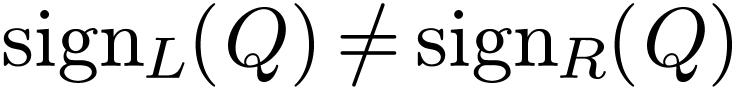 , whence that
, whence that 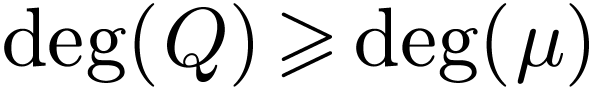 . But then
. But then 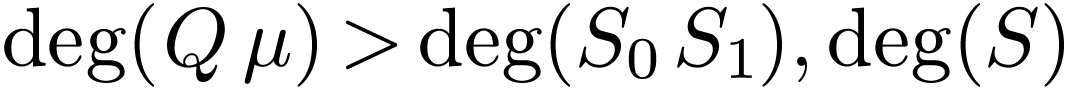 : a contradiction. We deduce that in fact
: a contradiction. We deduce that in fact 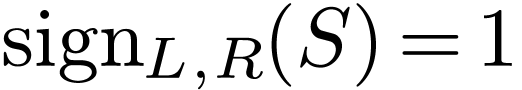 , which proves that
, which proves that  is a positive cone on
is a positive cone on 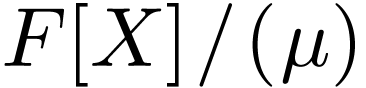 .
.
I write 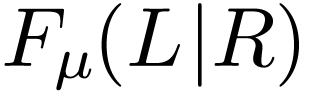 for the corresponding ordered
field. Similar arguments as in Proposition 3.4 yield:
for the corresponding ordered
field. Similar arguments as in Proposition 3.4 yield:
Proposition 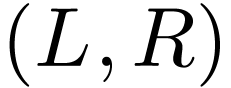 is unfilled and has a minimal polynomial
is unfilled and has a minimal polynomial 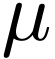 , then
, then 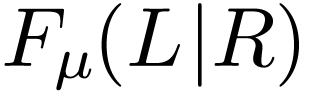 is
an ordered field extension of
is
an ordered field extension of  where
where 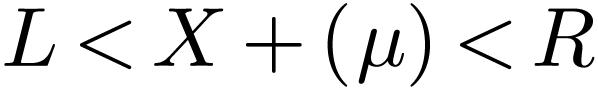 .
.
Lemma 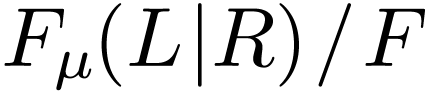 is cofinal.
is cofinal.
Sketch of Proof. This is a corollary of Lemma 2.1.
Any linearly oredered set enjoys a topology, called the order topology,
whose open sets are arbitrary unions of open intervals. An ordered field
 , equipped with the order
topology, is a topological field, i.e. the sum and product functions are
continuous for the product topology on
, equipped with the order
topology, is a topological field, i.e. the sum and product functions are
continuous for the product topology on  ,
whereas the additive inverse and multiplicative inverse functions are
continuous on their respective domains. A subset
,
whereas the additive inverse and multiplicative inverse functions are
continuous on their respective domains. A subset 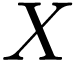 of
of 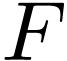 is dense in
is dense in 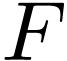 as a
linear order if and only if it is dense in
as a
linear order if and only if it is dense in 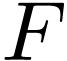 as a
topological space, i.e. if and only if for all
as a
topological space, i.e. if and only if for all 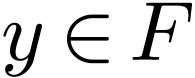 and all
and all 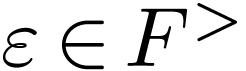 , there is an
, there is an 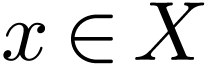 with
with 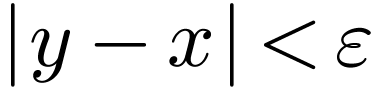 .
.
Definition
Remark  with a uniform structure as per [1,
Chapter 2], derived from its ordering. Then the notions of Cauchy
sequence, completeness and Cauchy-completion have equivalents in the
language of uniform structures, which are more general but more
involved.
with a uniform structure as per [1,
Chapter 2], derived from its ordering. Then the notions of Cauchy
sequence, completeness and Cauchy-completion have equivalents in the
language of uniform structures, which are more general but more
involved.
Definition
4.1. those are sometimes called Veronese cuts [2]
or Dedekind cuts or...
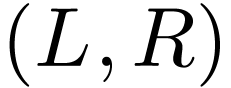 in an ordered field
in an ordered field  is
good
is
good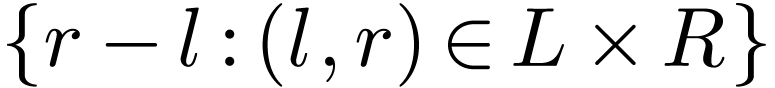 is coinitial in
is coinitial in  .
.
Note that any filled cut is good, and that a good cut 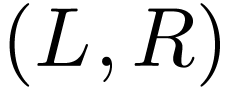 must satisfy in particular
must satisfy in particular 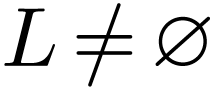 and
and 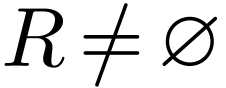 .
.
Lemma  be an ordered field, and let
be an ordered field, and let 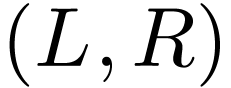 be a good, unfilled cut. If
be a good, unfilled cut. If 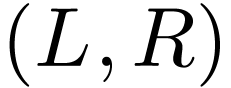 has no annihilator
polynomial, then
has no annihilator
polynomial, then 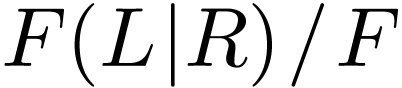 is a dense extension.
is a dense extension.
Sketch of Proof. Assume that 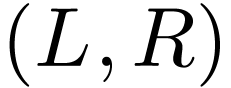 has no annihilator polynomial. So
has no annihilator polynomial. So 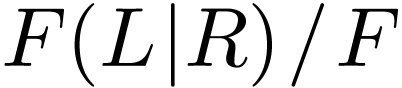 is a proper
ordered field extension. We claim that it is dense. It is cofinal by
Lemma 3.8, so we need only prove that for all
is a proper
ordered field extension. We claim that it is dense. It is cofinal by
Lemma 3.8, so we need only prove that for all 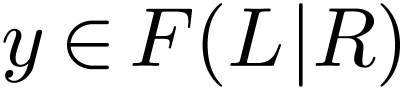 and
and 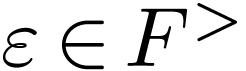 , there is
an
, there is
an 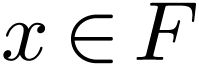 with
with 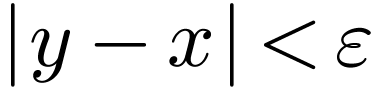 .
Write
.
Write 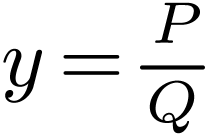 where
where 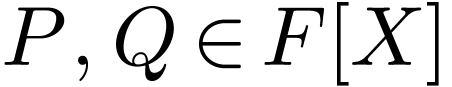 and
and 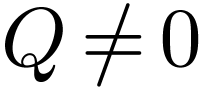 . In
. In 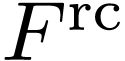 ,
the rational function
,
the rational function 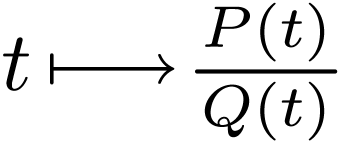 is uniformly continuous on
any bounded interval not containing its poles (indeed this is true in
is uniformly continuous on
any bounded interval not containing its poles (indeed this is true in
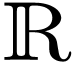 ). In particular, given
). In particular, given 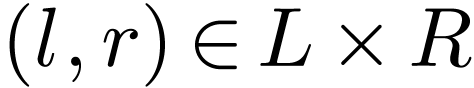 , there is a
, there is a 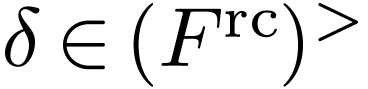 such that for all
such that for all 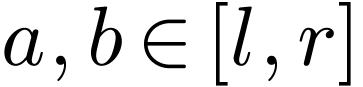 with
with 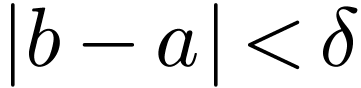 , we have
, we have 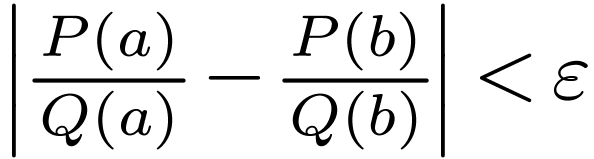 .
Since
.
Since  is cofinal, we may assume that
is cofinal, we may assume that  . Pick
. Pick  with
with
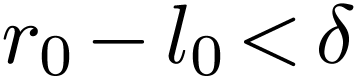 . So for all
. So for all 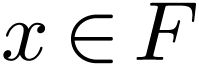 and with
and with 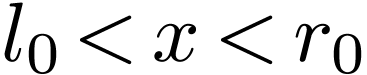 , we have
, we have 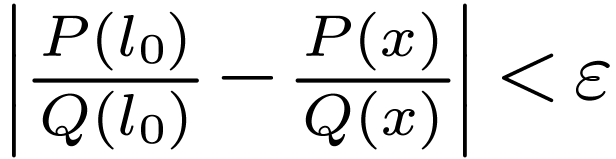 . Setting
. Setting 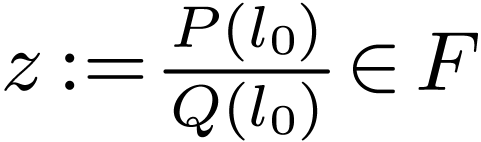 , this implies that
, this implies that 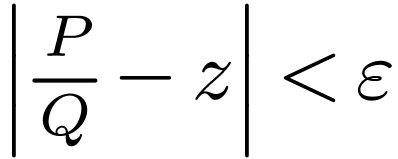 in
in  .
.
By similar arguments, we have:
Lemma  be an ordered field, and let
be an ordered field, and let  be a good, unfilled cut. If
be a good, unfilled cut. If 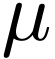 is a minimal
polynomial of
is a minimal
polynomial of 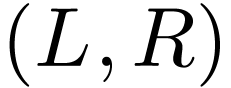 , then
, then 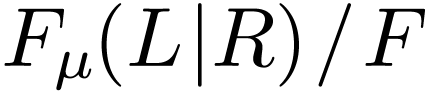 is a dense extension.
is a dense extension.
Proposition  is complete if and only if every
good cut in
is complete if and only if every
good cut in  is filled.
is filled.
Sketch of Proof. Assume that  is
complete and assume for contradiction that
is
complete and assume for contradiction that 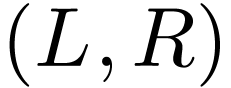 is a
good unfilled cut. So by Lemmas 4.4 and 4.5,
we have a proper dense extension of
is a
good unfilled cut. So by Lemmas 4.4 and 4.5,
we have a proper dense extension of  :
a contradiction. Conversely, consider a proper dense extension
:
a contradiction. Conversely, consider a proper dense extension 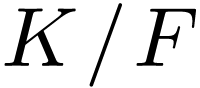 and fix a
and fix a 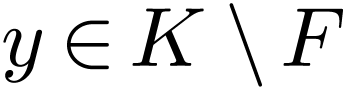 .
Since
.
Since 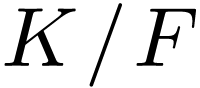 is cofinal, we have an unfilled cut
is cofinal, we have an unfilled cut 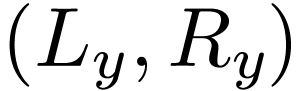 of Lemma 3.2. By density, given
of Lemma 3.2. By density, given 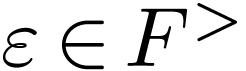 , there are
, there are 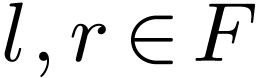 with
with 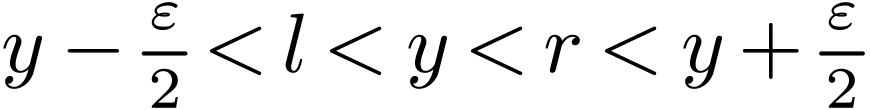 . So
. So 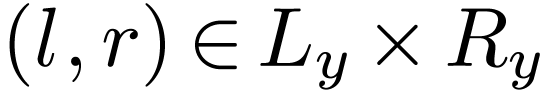 and
and 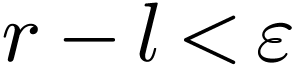 . This proves that
. This proves that 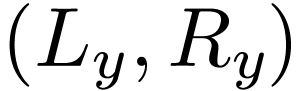 is good, hence the result.
is good, hence the result.
In this section, we fix an orderd field 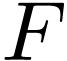 .
.
A sequence in 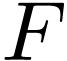 is a map
is a map 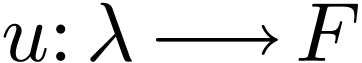 where
where 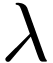 is a non-zero limit
ordinal.
is a non-zero limit
ordinal.
Definition  is a sequence
is a sequence 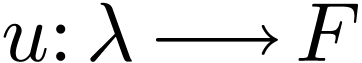 such that there is
an
such that there is
an 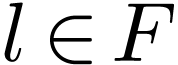 with
with
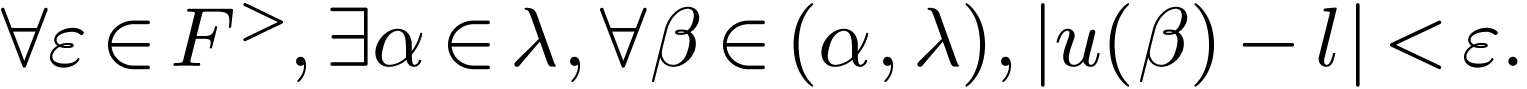
Saying that 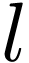 is a limit of
is a limit of 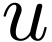 is the same as saying that the map
is the same as saying that the map 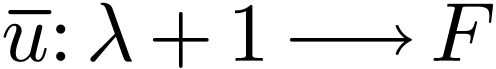 extending
extending
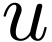 with
with 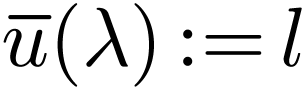 is continuous. As a
consequence of the fact that the topological space
is continuous. As a
consequence of the fact that the topological space 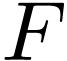 is Hausdorff, we have:
is Hausdorff, we have:
Lemma 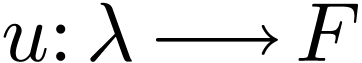 has at most one limit.
has at most one limit.
Definition  is a sequence
is a sequence 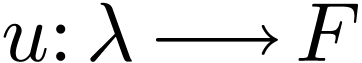 such that
such that
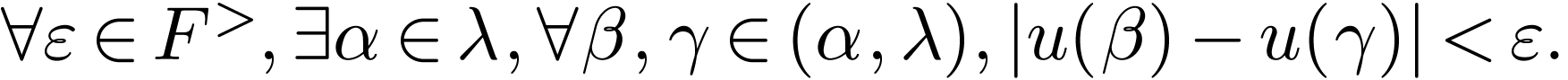
Lemma  is Cauchy.
is Cauchy.
Sketch of Proof. Pick 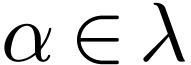 such that
such that
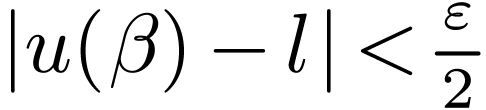 for all
for all 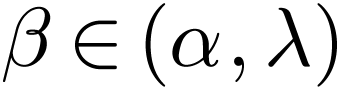 ,
then use the triangle inequality.
,
then use the triangle inequality.
Conversely, some Cauchy sequences are not convergent: take a Cauchy
sequence of rationnal numbers in the usual sense, whose limit in 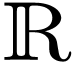 is irrational.
is irrational.
One can skip this subsection since it is not used in the sequel. However
the result written as Lemma 5.5 is quite useful when
working with Cauchy sequences. Recall that the cofinality of a linear
order 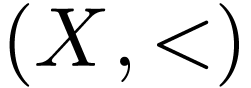 is equivalently
is equivalently
the unique regular ordinal which embeds cofinally (without strict
upper bound) into 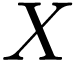 ;
;
the least ordinal which embeds cofinally into 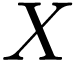 ;
;
the least cardinal of a cofinal subset of 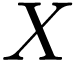 .
.
Moreover, two linear orders 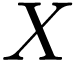 and
and 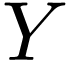 have the same cofinality if and only if there is a non-decreasing map
have the same cofinality if and only if there is a non-decreasing map
 whose range is cofinal in
whose range is cofinal in 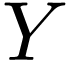 .
.
Lemma 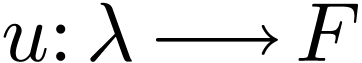 is a Cauchy sequence in
is a Cauchy sequence in  and
and
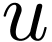 is not eventually constant, then
is not eventually constant, then 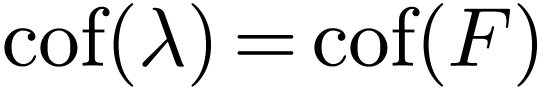 .
.
Sketch of Proof. By not eventually constant, I mean
that for all 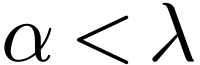 , there is a
, there is a
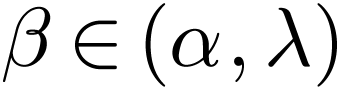 with
with 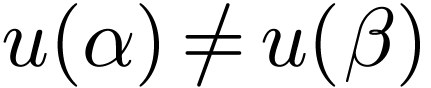 .
We will define a cofinal embedding
.
We will define a cofinal embedding 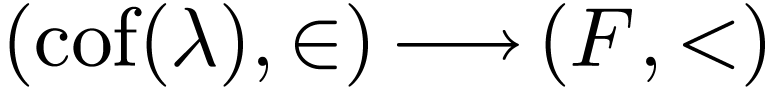 .
First pick cofinal embeddings
.
First pick cofinal embeddings 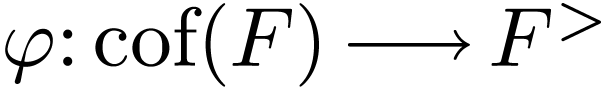 and
and 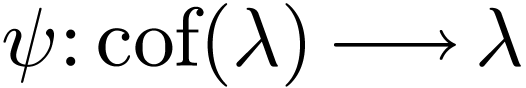 . For all
. For all 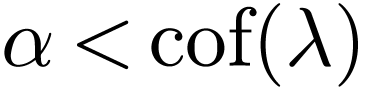 ,
we write
,
we write 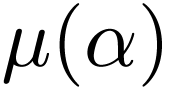 for the least ordinal in
for the least ordinal in 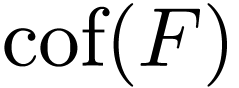 such that
such that 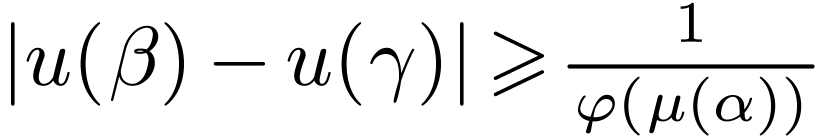 for some
for some 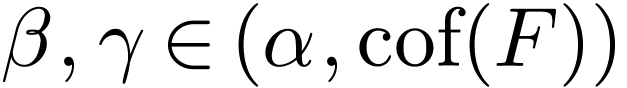 . This exists because
. This exists because  is not eventually constant and the range of
is not eventually constant and the range of 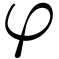 is
cofinal in
is
cofinal in  . Note that
. Note that 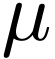 is non-decreasing. Now since
is non-decreasing. Now since 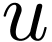 is Cauchy and
is Cauchy and 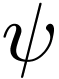 is a cofinal embedding, for all
is a cofinal embedding, for all
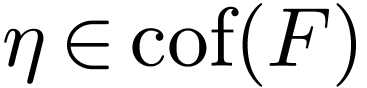 , there is an
, there is an 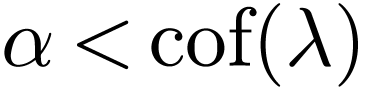 with
with 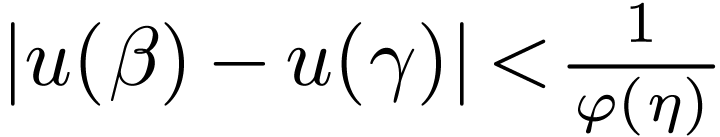 for all
for all 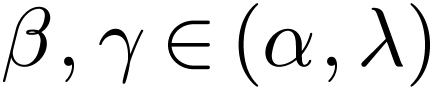 , whence
, whence 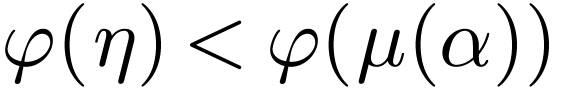 .
But
.
But 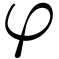 is strictly increasing, so
is strictly increasing, so 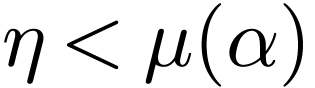 . This proves that the range of is cofinal in
. This proves that the range of is cofinal in
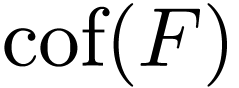 , hence
, hence 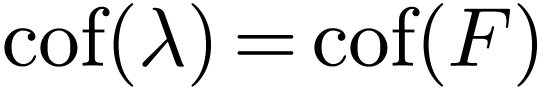 .
.
If 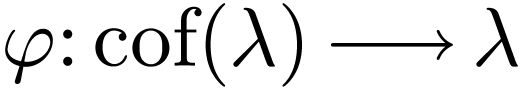 is a strictly increasing and cofinal map
(i.e. a map whose range is cofinal), then say that
is a strictly increasing and cofinal map
(i.e. a map whose range is cofinal), then say that  is a subsequence of
is a subsequence of 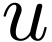 .
Note that subseqences of convergent/Cauchy sequences are
convergent/Cauchy, and that the limit is preserved in the convergent
case. The previous lemma shows that some properties of Cauchy sequences
can be reduced to those of Cauchy sequences indexed by
.
Note that subseqences of convergent/Cauchy sequences are
convergent/Cauchy, and that the limit is preserved in the convergent
case. The previous lemma shows that some properties of Cauchy sequences
can be reduced to those of Cauchy sequences indexed by 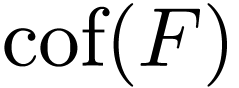 .
.
Definition  is said
Cauchy-complete if every Cauchy
sequence in
is said
Cauchy-complete if every Cauchy
sequence in  converges.
converges.
Proposition  is Cauchy-complete if and only if
it its good cuts are filled.
is Cauchy-complete if and only if
it its good cuts are filled.
Sketch of Proof. Fix a cofinal embedding 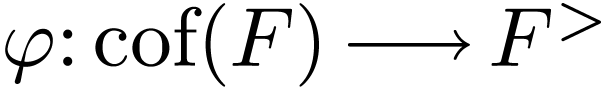 . Assume that
. Assume that  is
Cauchy-complete and assume for contradiction that there is a good,
unfilled cut
is
Cauchy-complete and assume for contradiction that there is a good,
unfilled cut 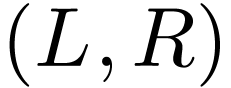 in
in  .
For all
.
For all 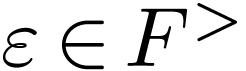 , there is an
, there is an 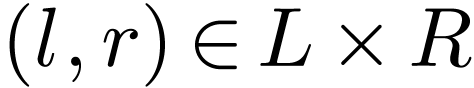 with
with 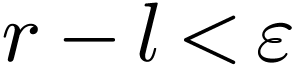 .
Since
.
Since 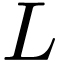 has no maximum, there is
has no maximum, there is 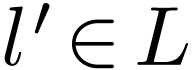 with
with 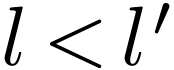 , whence
, whence 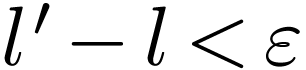 . Using this, we define a strictly increasing
sequence
. Using this, we define a strictly increasing
sequence 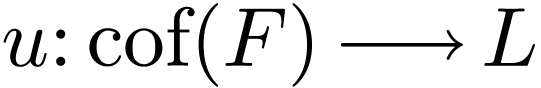 such that for all
such that for all 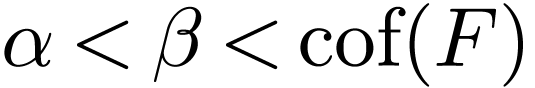 and
and 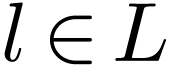 with
with 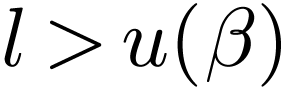 ,
we have
,
we have
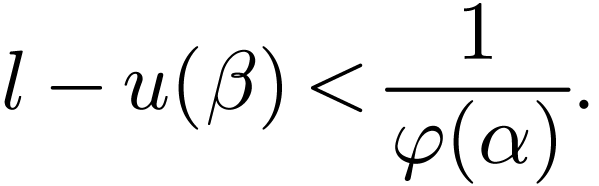 |
(5.1) |
Assume that 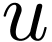 is defined on
is defined on 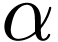 and that
and that 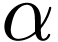 is a limit. Assume for contradiction
that
is a limit. Assume for contradiction
that 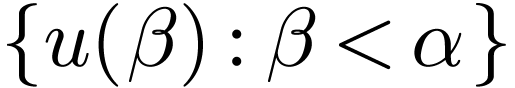 is cofinal in
is cofinal in 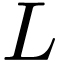 .
Note that
.
Note that 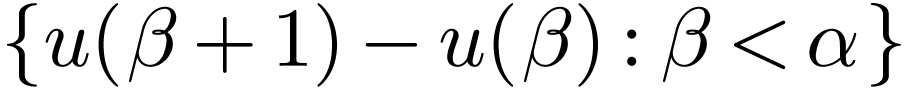 has a strict lower bound
has a strict lower bound  in
in  since its cardinality is
since its cardinality is 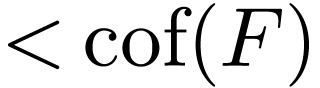 . Consider
. Consider 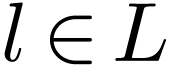 with
with 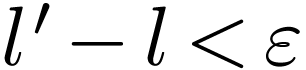 for all
for all 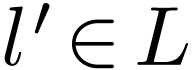 with
with 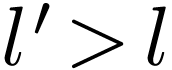 . We find a
. We find a 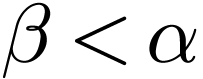 with
with 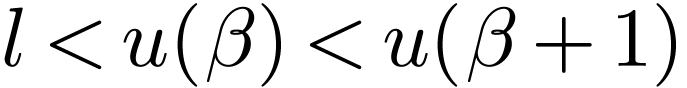 , so
, so 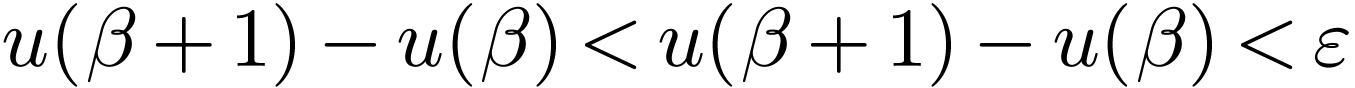 : a contradiction. So
: a contradiction. So 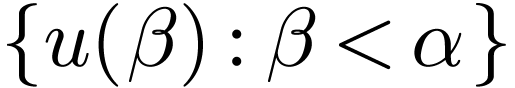 has a strict upper bound
has a strict upper bound 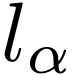 in
in 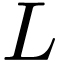 . We pick
. We pick 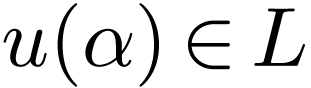 with
with 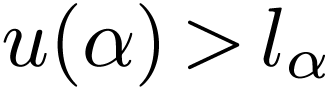 and
and 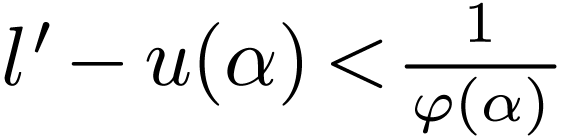 for all
for all 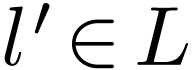 with
with 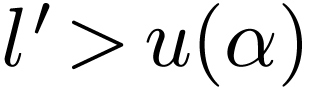 and extend the sequence accordingly. For
successor
and extend the sequence accordingly. For
successor 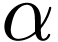 , we extend
, we extend 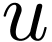 directly.
directly.
So 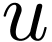 is strictly increasing, ranges in
is strictly increasing, ranges in 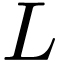 and satisfies (5.1) by definition. Note that
this implies that
and satisfies (5.1) by definition. Note that
this implies that 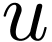 is a Cauchy sequence. Let
is a Cauchy sequence. Let 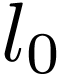 be its limit in
be its limit in  .
We claim that
.
We claim that 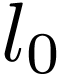 is the maximum of
is the maximum of 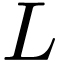 . Indeed assume that
. Indeed assume that 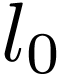 has a strict upper bound
has a strict upper bound 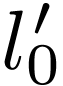 in
in 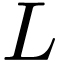 . Set
. Set 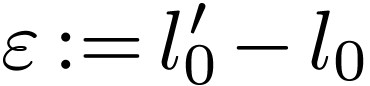 ,
and fix
,
and fix 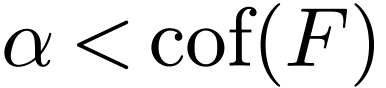 with
with 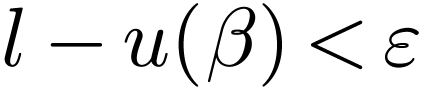 for all
for all
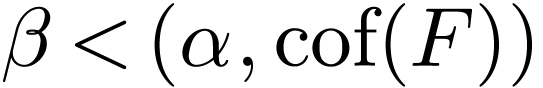 and
and 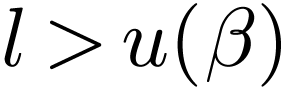 in
in 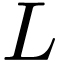 . It is easy to see that
. It is easy to see that 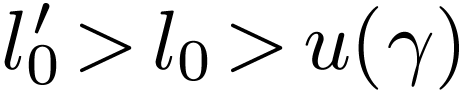 for all
for all 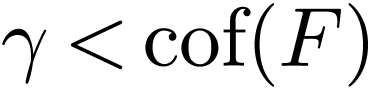 . So
. So 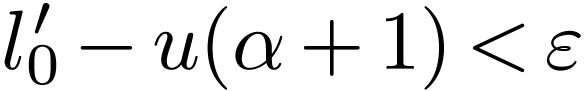 , whence
, whence 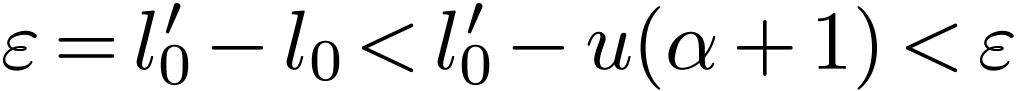 :
a contradiction.
:
a contradiction.
So 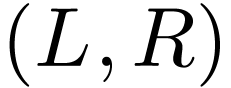 is filled: a contradiction.
is filled: a contradiction.
Conversely, assume that every good cut in  is
filled and that
is
filled and that  is not Cauchy-complete. Let
is not Cauchy-complete. Let  be a non-convergent Cauchy sequence. Write
be a non-convergent Cauchy sequence. Write
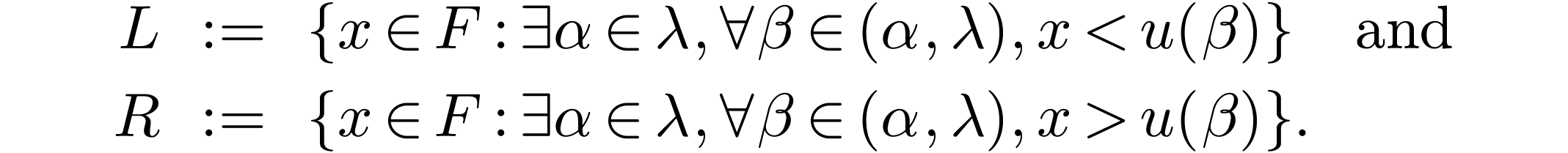
I claim that this is a cut. We have 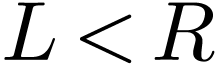 by
definition. For
by
definition. For 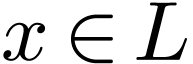 and corresponding
and corresponding 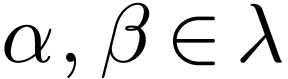 , the element
, the element 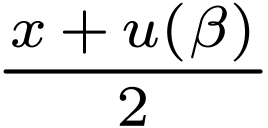 is a
strict upper bound of
is a
strict upper bound of 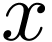 in
in 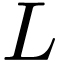 . So
. So 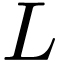 has no maximum, and
likewise
has no maximum, and
likewise 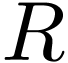 has no minimum. Now consider
has no minimum. Now consider 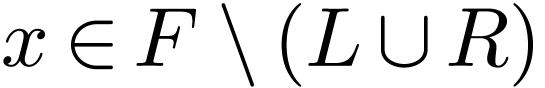 . Since
. Since 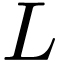 is
an initial segment of
is
an initial segment of  whereas
whereas 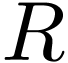 is a final segment of
is a final segment of  , we in
fact have
, we in
fact have 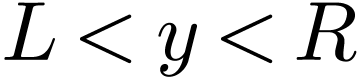 . Let
. Let 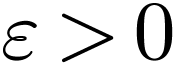 , and let
, and let 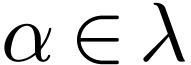 with
with 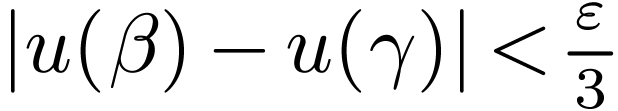 for all
for all 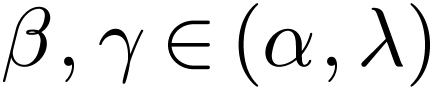 .
Since
.
Since 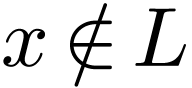 and
and 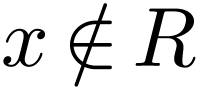 ,
there are
,
there are 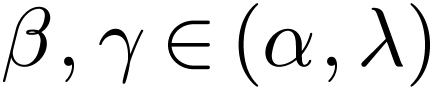 with
with 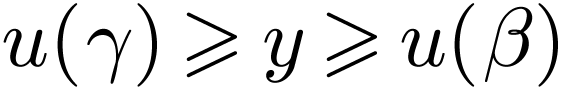 .
We deduce that for all
.
We deduce that for all 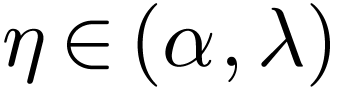 , we
have
, we
have
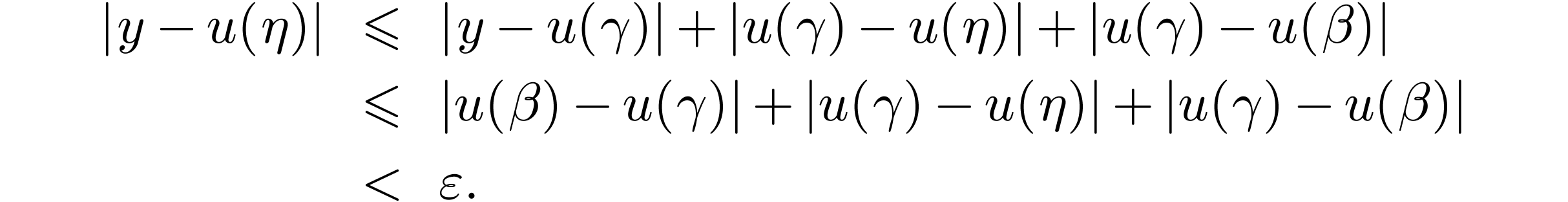
So 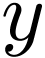 is the limit of
is the limit of 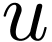 ,
which contradicts our assumption on
,
which contradicts our assumption on 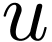 .
We deduce that
.
We deduce that 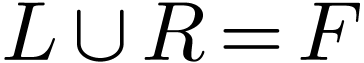 , hence
, hence  is an unfilled cut. The fact that
is an unfilled cut. The fact that 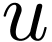 is Cauchy implies that
is Cauchy implies that 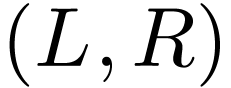 is good: a
contradiction.
is good: a
contradiction.
Proposition
Sketch of Proof. This follows from Propositions 5.7 and 4.6.
Proposition  be an ordered field. There is a dense, complete extension
of
be an ordered field. There is a dense, complete extension
of  .
.
There are several distinct ways to prove of this:
Use Dedekind's construction of the reals by means of operations on
cuts, where instead of cuts of rational numbers, one considers
good cuts in 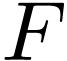 .
This directly yields the extension, but it is somewhat tedious.
.
This directly yields the extension, but it is somewhat tedious.
Use Cauchy's construction of the reals by means of Cauchy sequence,
where instead of standard sequences, one considers 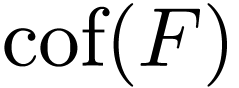 -indexed Cauchy sequences. This is also
tedious.
-indexed Cauchy sequences. This is also
tedious.
Use Zorn's lemma and some abstract nonsense. This is shorter, which is why I will proceed thus.
Sketch of Proof. So let 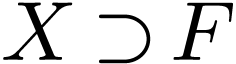 be a
set of cardinality
be a
set of cardinality 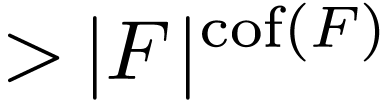 . Let
. Let  denote the set of dense ordered field extensions
denote the set of dense ordered field extensions 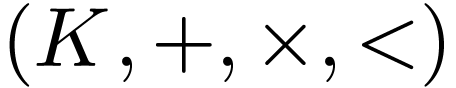 of
of  where
where 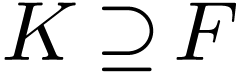 is a subset of
is a subset of 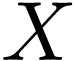 . We endow
. We endow
 with the extension ordering:
with the extension ordering: 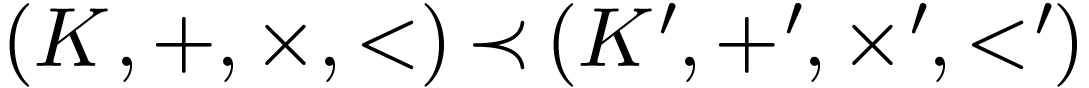 if
if 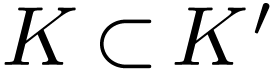 and the operations and ordering on
and the operations and ordering on 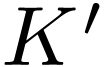 extend those on
extend those on 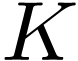 .
This set contains
.
This set contains 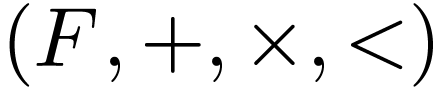 , and it is
inductive since we can take increasing unions. By Zorn's lemma, the set
, and it is
inductive since we can take increasing unions. By Zorn's lemma, the set
 has a maximal element
has a maximal element 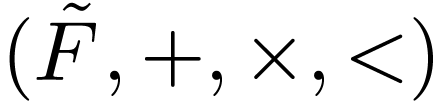 . I claim that
. I claim that 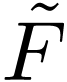 is complete.
Assume that it is not complete. So it has a proper dense extension
is complete.
Assume that it is not complete. So it has a proper dense extension  . Now as we've seen every element
of
. Now as we've seen every element
of  injectively yields an unfilled good cut in
injectively yields an unfilled good cut in
 , and a (Cauchy) sequence
, and a (Cauchy) sequence
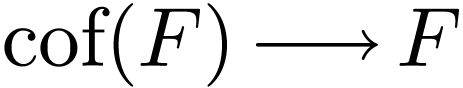 . So we have an injection
. So we have an injection
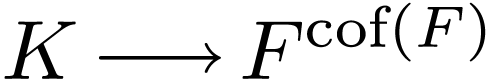 . Likewise, there is an
injection
. Likewise, there is an
injection 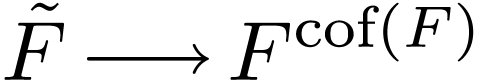 . In particular,
. In particular,
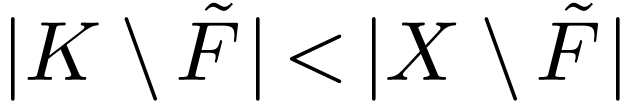 , so there is an injection
, so there is an injection
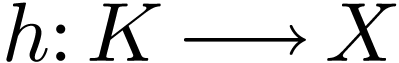 with
with 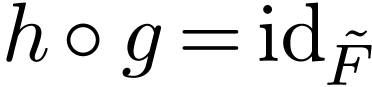 .
Using this, we obtain an isomorphic copy of
.
Using this, we obtain an isomorphic copy of 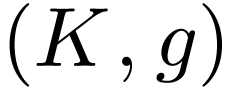 into
into
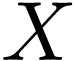 which extends the inclusion
which extends the inclusion  . This contradicts the maximality of
. This contradicts the maximality of 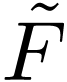 . So
. So 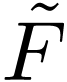 is in
fact complete.
is in
fact complete.
Theorem 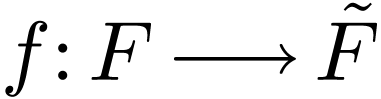 be a dense embedding into a complete extension. If
be a dense embedding into a complete extension. If 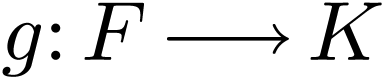 is a cofinal extension and
is a cofinal extension and 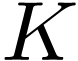 is
complete, then there is a unique embedding
is
complete, then there is a unique embedding 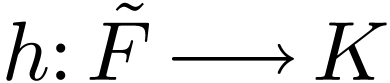 with
with
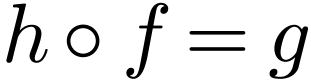 .
.
Sketch of Proof. Fix such an extension 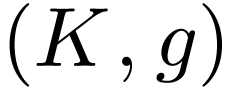 . Let
. Let 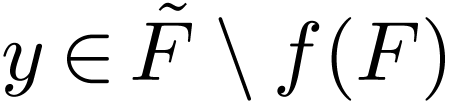 .
We have a corresponding unfilled cut
.
We have a corresponding unfilled cut 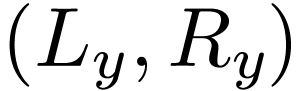 in
in  by Lemma 3.2, which as we saw in the
proof of Proposition 4.6 is a good cut.
by Lemma 3.2, which as we saw in the
proof of Proposition 4.6 is a good cut.
I claim that there is a unique element 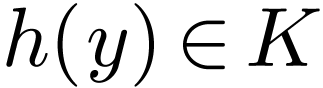 with
with
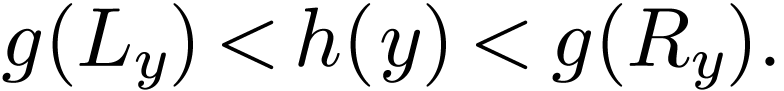 |
(6.1) |
The unicity follows from the fact that 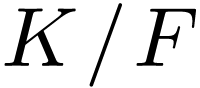 is
cofinal, indeed for
is
cofinal, indeed for 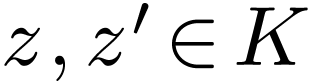 with
with 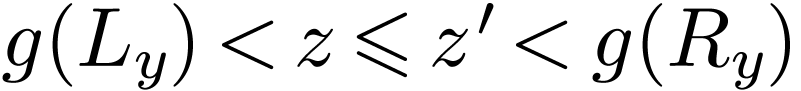 , we have
, we have 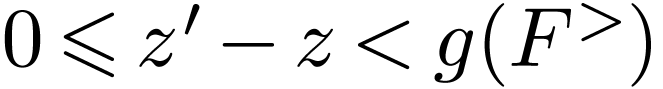 since
since 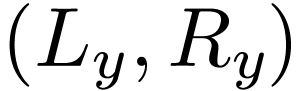 is good. But since
is good. But since 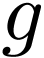 is a cofinal
embedding, it follows that
is a cofinal
embedding, it follows that 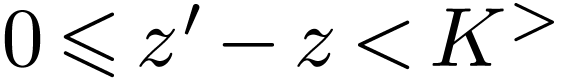 ,
whence that
,
whence that 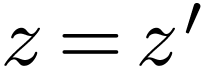 . Assume for
contradiction that no such element
. Assume for
contradiction that no such element 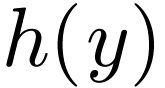 exists. Write
exists. Write
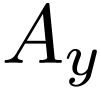 (resp.
(resp. 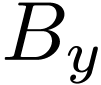 )
for the set of lower bounds (resp. upper bounds) of elements of
)
for the set of lower bounds (resp. upper bounds) of elements of 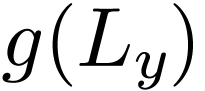 . We will prove that
. We will prove that 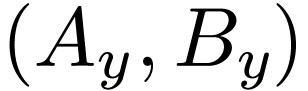 is a good unfilled cut in
is a good unfilled cut in 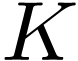 ,
contradicting the completeness of
,
contradicting the completeness of 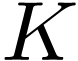 .
It is clear that
.
It is clear that 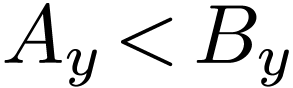 . Since
. Since 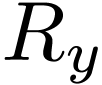 has no minimum, neither do
has no minimum, neither do 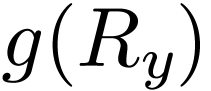 and thus
and thus 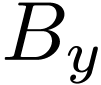 . Likewise
. Likewise 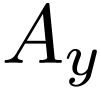 has no maximum. It remains to show that
has no maximum. It remains to show that 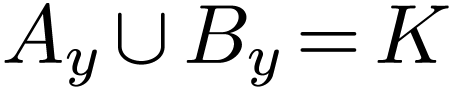 . Assume that there is a
. Assume that there is a 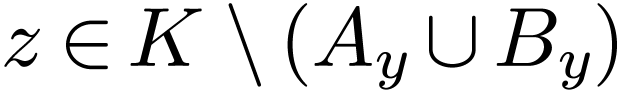 . By definition of
. By definition of 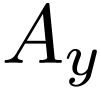 and
and 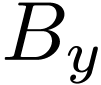 , we must have
, we must have 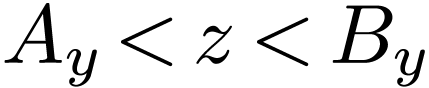 . It follows that
. It follows that 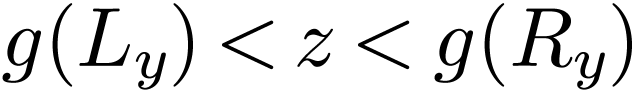 :
a contradiction. So
:
a contradiction. So 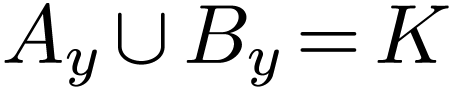 , which
concludes our proof that
, which
concludes our proof that 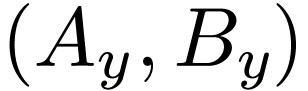 is an unfilled cut in
is an unfilled cut in
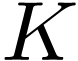 and thus our proof by contradiction of the
existence and unicity of
and thus our proof by contradiction of the
existence and unicity of 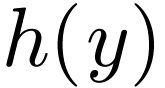 .
.
We complete our definition of the map 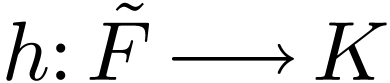 by setting
by setting
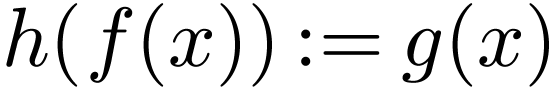 for all
for all 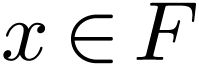 .
For
.
For 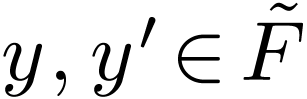 with
with 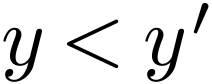 ,
there is an
,
there is an 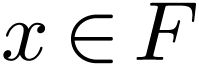 with
with 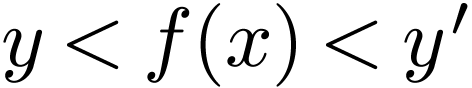 .
It follows from the definition of
.
It follows from the definition of 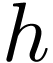 that
that  , whence
, whence 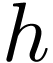 is
strictly increasing. Note that
is
strictly increasing. Note that 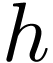 is the only
strictly increasing map
is the only
strictly increasing map 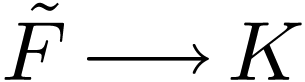 with
with 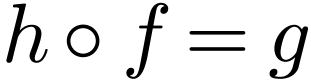 , since any such map must satisfy the defining
inequality (6.1). So it is enough to conclude to prove that
, since any such map must satisfy the defining
inequality (6.1). So it is enough to conclude to prove that
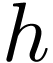 is a morphism of rings. Since
is a morphism of rings. Since 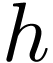 coincides with
coincides with 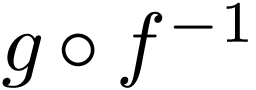 on
on 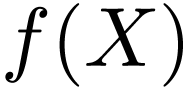 ,
we need only prove that
,
we need only prove that 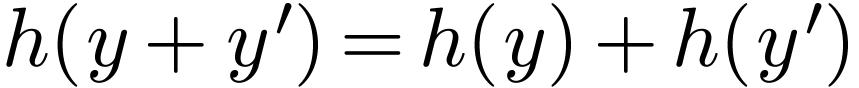 and
and 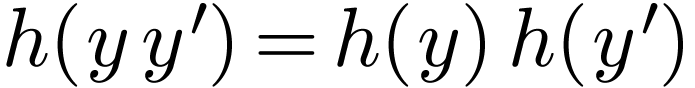 for all
for all 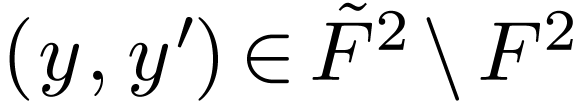 .
.
For 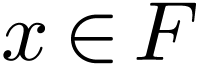 and
and 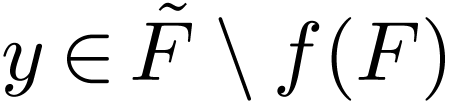 ,
we have
,
we have 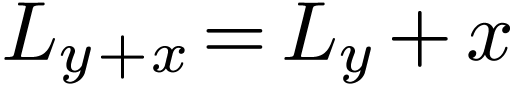 and
and 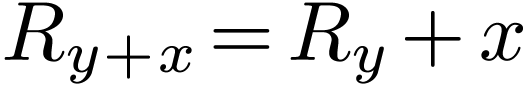 ,
so
,
so 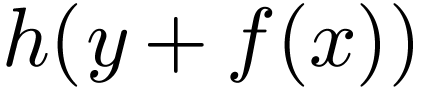 and
and 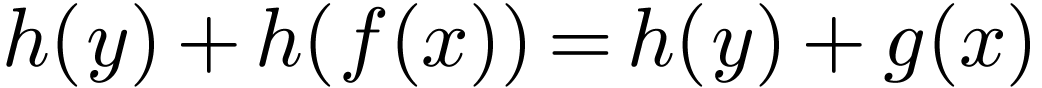 are both the
unique element
are both the
unique element 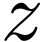 of
of 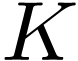 with
with
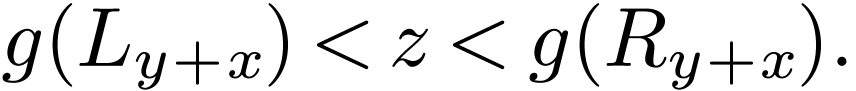
It follows that 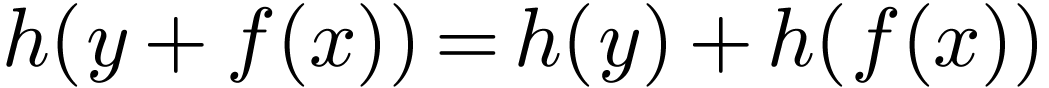 . Now let
. Now let
 . Again the element
. Again the element 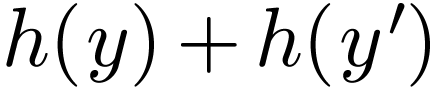 is unique with
is unique with 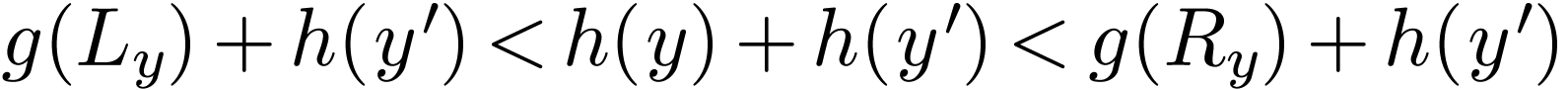 .
But by the previous argument, we also have
.
But by the previous argument, we also have
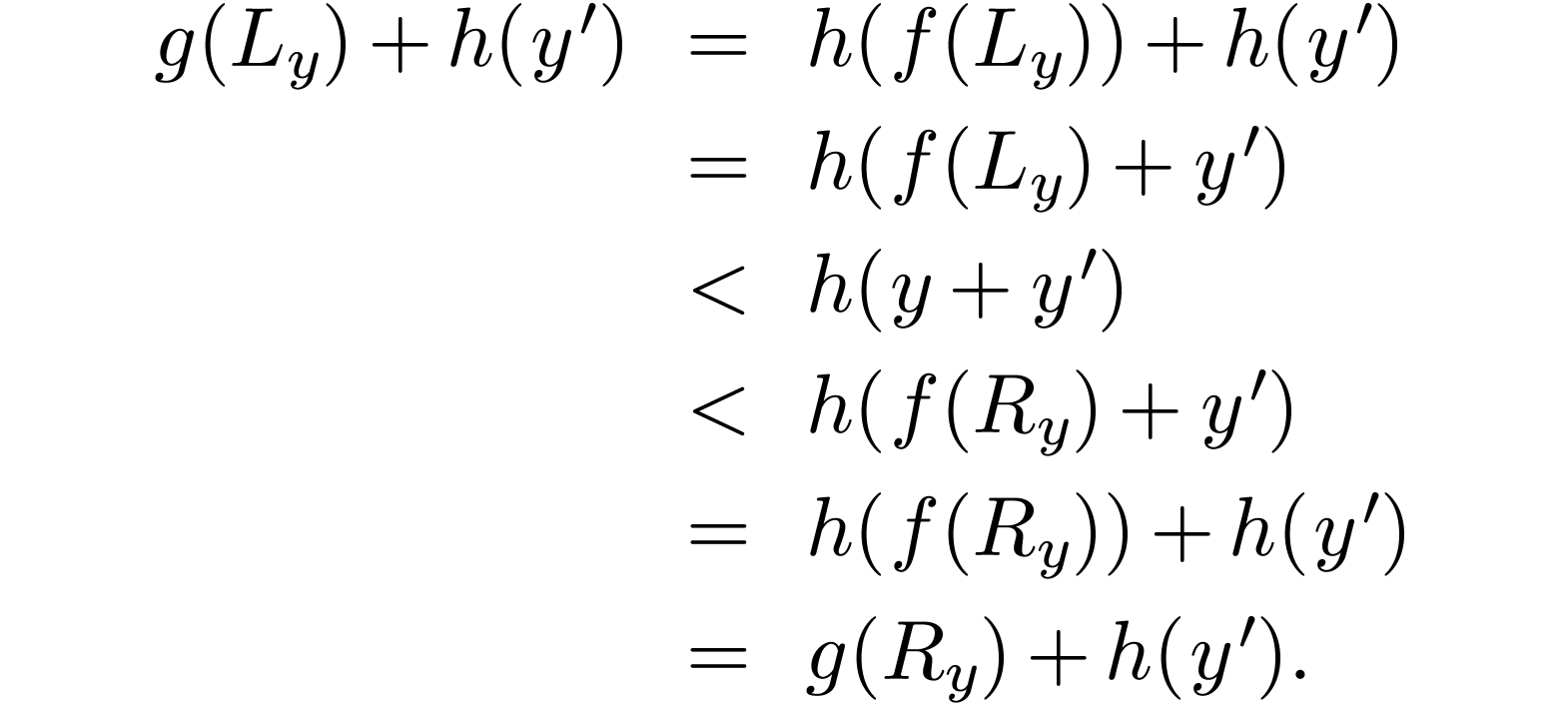
So 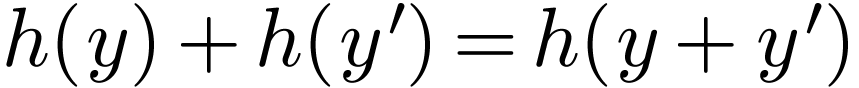 , i.e.
, i.e. 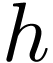 is a group morphism. It follows that in order to deal with the product,
we need only consider the case of products of strictly positive
elements. For those, similar arguments as those used for the sum yield
the result. This concludes the (sketch of) proof.
is a group morphism. It follows that in order to deal with the product,
we need only consider the case of products of strictly positive
elements. For those, similar arguments as those used for the sum yield
the result. This concludes the (sketch of) proof.
The extension 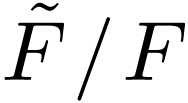 is called the
completion (or Cauchy completion) of
is called the
completion (or Cauchy completion) of 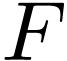 . It is unique up to unique isomorphism.
. It is unique up to unique isomorphism.
So you can see a similarity between the completion operator 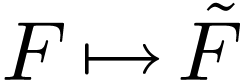 and the real closure operator
and the real closure operator 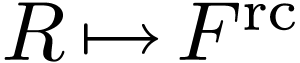 . First of all those are both functors, from the
category of ordered fields with cofinal embeddings and the category of
ordered fields with embeddings respectively, to their full subcategory
of complete and real-closed fields respectively. They are also both left
adjoints to the forgetful functors.
. First of all those are both functors, from the
category of ordered fields with cofinal embeddings and the category of
ordered fields with embeddings respectively, to their full subcategory
of complete and real-closed fields respectively. They are also both left
adjoints to the forgetful functors.
Moreover, an ordered field is real-closed if it has no proper algebraic extension, complete if it has no proper dense extension. We also have the following analogy:
Completion: |
Real closure: |
minimal cofinal and complete extension |
minimal real-closed extension |
maximal dense extension |
maximal algebraic extension |
Finally, there is a non-trivial interaction between those two closure
operators, which is that the completion of a real-closed field is
real-closed, or equivalently 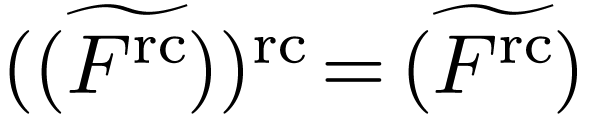 for any ordered
field
for any ordered
field  . This can be shown by
lifting the theorem of continuity of roots (for polynomials), which is
valid in
. This can be shown by
lifting the theorem of continuity of roots (for polynomials), which is
valid in  , to arbitrary
real-closed fields, using Tarski's theorem.
, to arbitrary
real-closed fields, using Tarski's theorem.
N. Bourbaki. Topologie générale (chapitres 1 à 4). Eléments de mathématique. Springer Berlin Heidelberg, 1971.
P. Ehrlich. The Rise of non-Archimedean Mathematics and the Roots of a Misconception I: The Emergence of non-Archimedean Systems of Magnitudes. Archive for History of Exact Sciences, 60(1):1–121, 2006.
I. Kaplansky. Maximal fields with valuations, ii. Duke Mathematical Journal, 12(2):243–248, 06 1945.
absolute value 2
algebraic extension 3
annihilator polynomial 4
Cauchy sequence 8
Cauchy-complete ordered field 9
(cofinal, dense) embedding 2
cofinal subset 1
(cofinal,dense) extension 2
complete ordered field 7
completion 10
convergent sequence 8
cut 4
dense subset 1
filled cut, unfilled cut 4
good cut 7
limit of a sequence 8
minimal polynomial 4
ordered domain 2
ordered field 2
positive cone 2
real closure 3
real-closed field 3
sequence 8
 set of strictly positive elements in
set of strictly positive elements in  2
2
 ordered fraction field of
ordered fraction field of  2
2
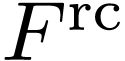 real closure of
real closure of  7 3
7 3
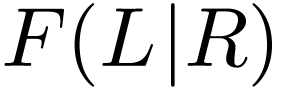 simple extension for
simple extension for  without annihilator polynomial 4
without annihilator polynomial 4
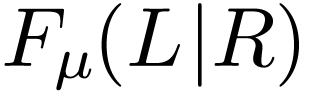 simple extension of the cut
simple extension of the cut 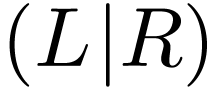 with minimal polynomial
with minimal polynomial 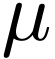 6
6