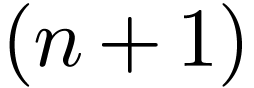 -th round, Alice sets forth
an ordinal
-th round, Alice sets forth
an ordinal 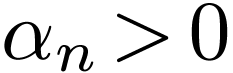 , then Bob
proposes an ordinal
, then Bob
proposes an ordinal 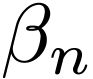 , with
the following constraints:
, with
the following constraints:
|
Késako?
Here's a game, entitled « non-standard gap », which lets you figure out if the person you're speaking to has a non-standard mind, or - and surely it's the same thing - if they're secretely a set theorist.
This is a two-player game where Alice and Bob play in turns. At the
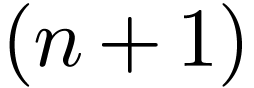 -th round, Alice sets forth
an ordinal
-th round, Alice sets forth
an ordinal 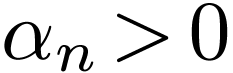 , then Bob
proposes an ordinal
, then Bob
proposes an ordinal 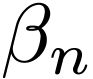 , with
the following constraints:
, with
the following constraints:
 |
(1) |
Alice loses the game in the  -th
round if Bob submits her a winning strategy, with proof that in less
than a determined number
-th
round if Bob submits her a winning strategy, with proof that in less
than a determined number 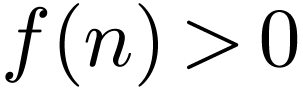 of rounds after this
of rounds after this
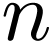 -th one, Alice won't be able
to extend her sequence while observing the constraints (that is, we'll
have
-th one, Alice won't be able
to extend her sequence while observing the constraints (that is, we'll
have 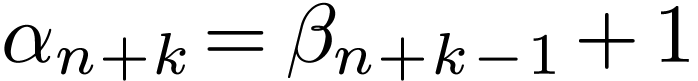 for a certain
for a certain  ).
Bob loses the game if he gives up or dies of thirst.
).
Bob loses the game if he gives up or dies of thirst.
Example. Alice plays the number 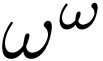 ;
;
Bob plays 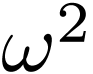 ;
;
Alice plays 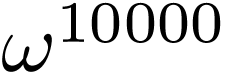 ;
;
Bob plays 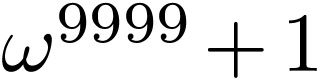 ;
;
Alice plays  ;
;
Bob plays 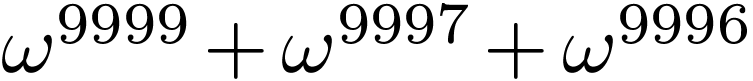 ;
;
Alice plays 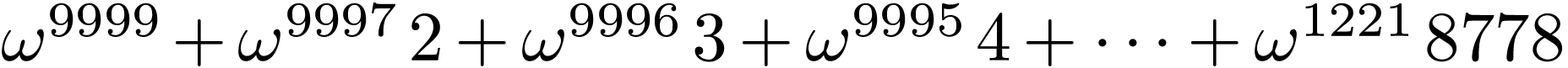 .
.
Bob then proposes the following winning strategy:
If Alice has just played the number
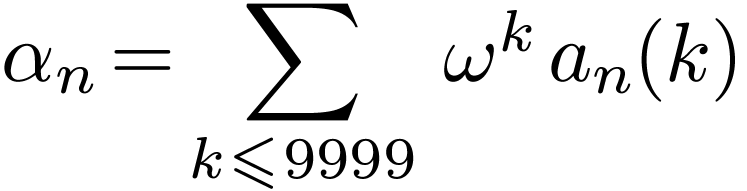
where 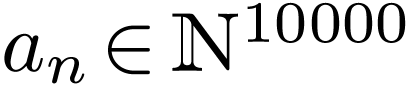 , then Bob will play
, then Bob will play
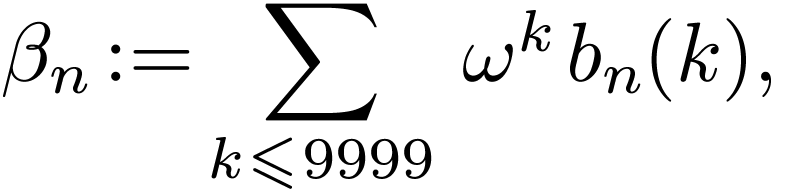
where 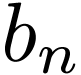 is the predecessor of
is the predecessor of 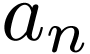 in
in 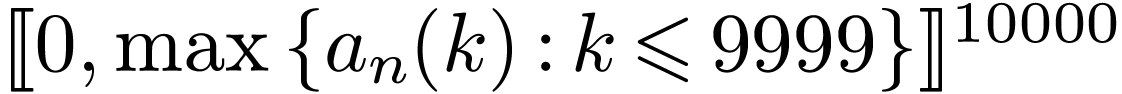 for the appropriate lexicographical ordering.
Bob claims, with proof, that Alice will lose in at most
for the appropriate lexicographical ordering.
Bob claims, with proof, that Alice will lose in at most 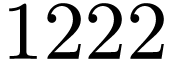 additional rounds.
additional rounds.
Question 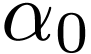 being fixed, does
Bob have a winning strategy? If not, then which is this ordinal
being fixed, does
Bob have a winning strategy? If not, then which is this ordinal 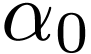 that is smallest, for which Bob has no winning
strategy?
that is smallest, for which Bob has no winning
strategy?
Question
Remark. I never lost a game of non-standard gap.