Abelian and non-Abelian ordered groups
|
|
There is a universal divisible extension  .
.
The theory of divisible Abelian ordered groups is the
model-completion of the theory of Abelian ordered groups. It has
QE and is o-minimal.
In the non-Abelian case, solving
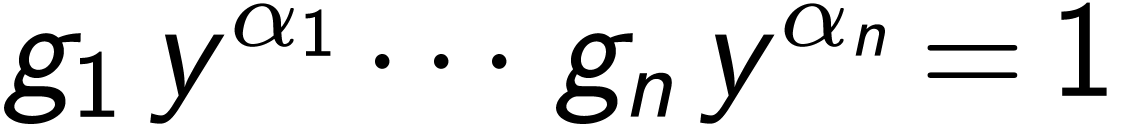
in extensions of  is
highly non-trivial (recall the functional representation of
is
highly non-trivial (recall the functional representation of  ...).
...).
Divisibility, conjugacy, problems
|
|
Question 1.
Is any ordered group contained in a divisible
one?
[Bludov, 2002] Yes if it is
metabelian.
[Bludov, 2005] No, in
general.
Question 2.
Is there an ordered group in which
any two strictly positive elements are conjugate?
Question 3.
Is there a first-order theory of ordered
groups which is complete and model complete, and has non-Abelian
models? [Pillay-Steinhorn,
1986]: such theory is not o-minimal.
An orderable group is a group  which can be ordered.
which can be ordered.
Every nilpotent torsion-free group is orderable.
Since orderable groups are closed under subgroups, isomorphism and
ultrapowers, they form an elementary class in the first-order
language  .
.
[Bludov, 2002] This class is
not finitely axiomatizable.
So any elementary class of ordered groups in 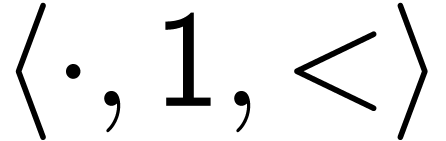 induces an elementary class in
induces an elementary class in 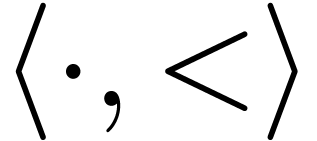 of thus orderable groups.
of thus orderable groups.
Miscellany about free groups
|
|
In the 40's, Tarski aksed whether free groups
have the same first-order theory, and if so, whether this theory is
decidable.
Both answers are positive [Sela,
2006] and [Kharlampovich-Myasnikov, 2006].
Free groups can always be ordered [Iwasawa, 1948],
and:
The free product of a family of groups can be ordered in such
a way as to preserve the ordering on each member of the
family.
Consider the following axioms for an ordered group  :
:
All Abelian ordered groups are growth order groups.
Question 4.
If  expands the real ordered field, then must
expands the real ordered field, then must  be a growth order group?
be a growth order group?
Differential fields of series and GOG
|
|
Idea: obtain GOG closed under certain equations
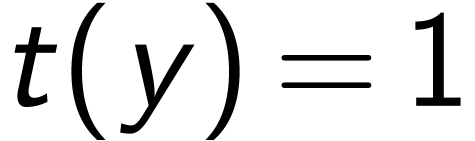 by constructing ordered
differential fields of formal series with composition laws:
by constructing ordered
differential fields of formal series with composition laws:
These operations extend to the ordered field  of formal Laurent series.
of formal Laurent series.
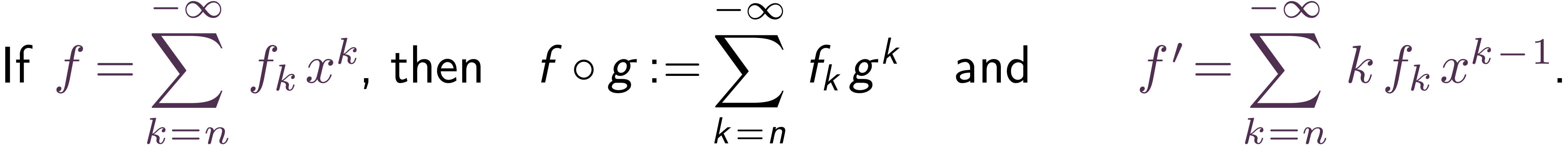
Problem: The ordered monoid 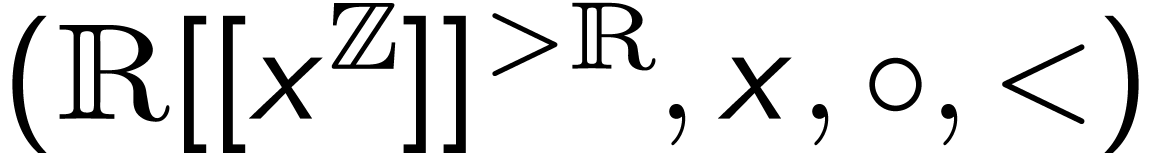 is not a group.
is not a group.  has no inverse
has no inverse
The operations extend to the field  of Puiseux series, and
of Puiseux series, and 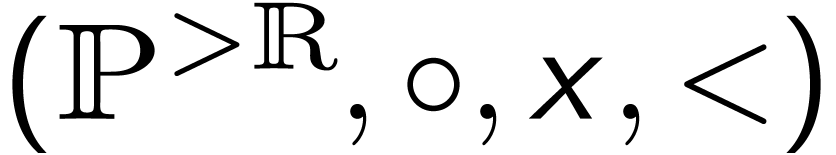 is a growth order group.
is a growth order group.
-
Is  divisible?
divisible?
We now look at the sructure 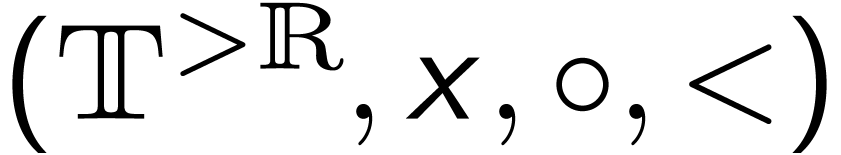 .
.
This is a right-ordered group, i.e for all 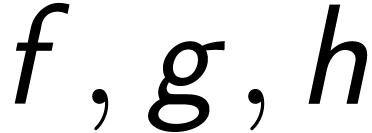 ,
,  .
.
This is a growth order group.
The group is not divisible since 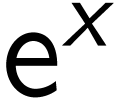 has no square root. There is no “half exponential” which
can be expressed as a combination of exponentials and logarithms.
However:
has no square root. There is no “half exponential” which
can be expressed as a combination of exponentials and logarithms.
However:
Any two 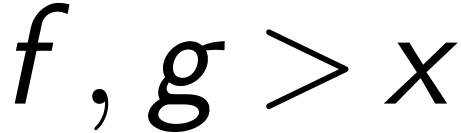 with
with
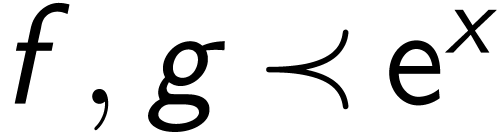 are conjugate.
are conjugate.
Conjucacy and Abel's equation
|
|
Question 5.
Can an o-minimal expansion of 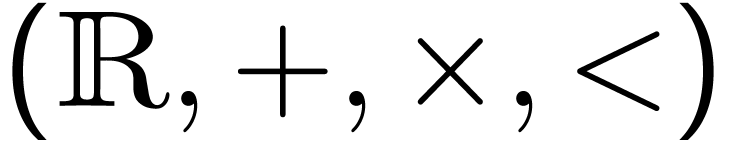 define a transexponential function?
define a transexponential function?
Using Taylor series arguments, one shows that:
The structure 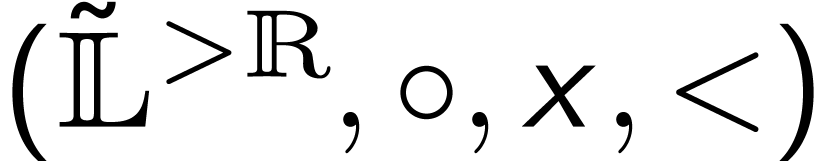 is
an ordered group.
is
an ordered group.
In the group 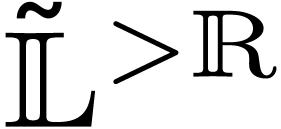 , all
conjugacy equations can now be solved:
, all
conjugacy equations can now be solved:
Using this, one shows that:
The structure 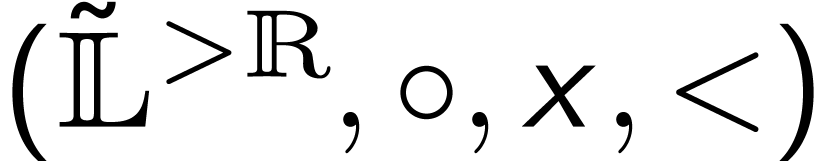 is
a growth order group.
is
a growth order group.
So we have a GOG solution to our Question 2
on ordered groups.
We have a simplest positive infinite number  corresponding to the ordinal
corresponding to the ordinal  and the series
and the series  .
.
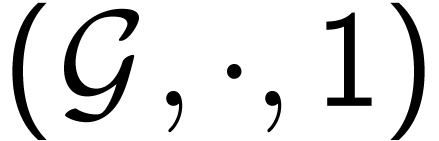 equipped with a linear
ordering
equipped with a linear
ordering  with
with

 .
.
 is an embedding
is an embedding  for
some linearly ordered set
for
some linearly ordered set  ,
where
,
where  is the
ordering by universal comparison.
is the
ordering by universal comparison.
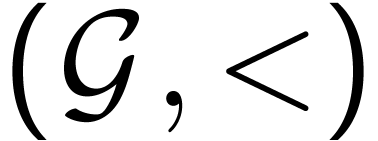 itself
with translations on the left, i.e.
itself
with translations on the left, i.e.  .
.
 is dense or
is dense or
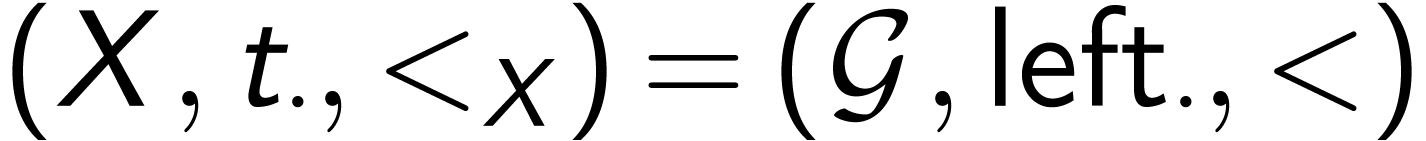 , then
, then 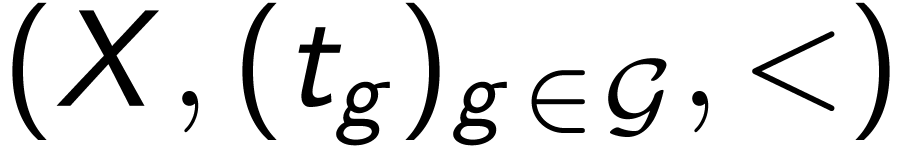 has QE and is o-minimal.
has QE and is o-minimal.

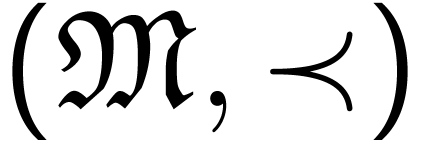 is a
linearly ordered set. Each
is a
linearly ordered set. Each  is represented as a series
is represented as a series  .
.
 be an ordered
field. Let
be an ordered
field. Let  be an
ordered vector space over
be an
ordered vector space over  is an ordered
group for the product
is an ordered
group for the product 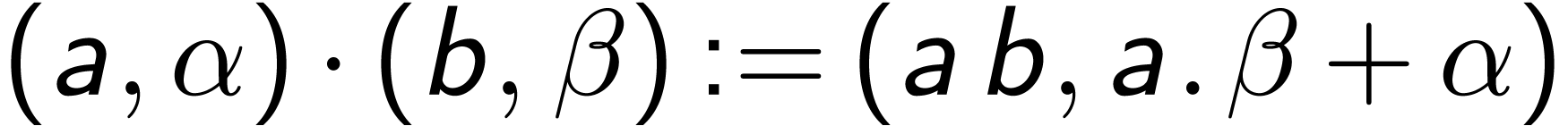 and the lexicographic ordering.
and the lexicographic ordering.
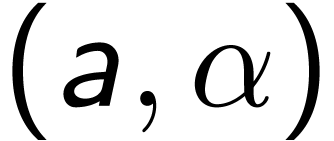 as
the strictly increasing affine map
as
the strictly increasing affine map  ,
and the ordering is then
,
and the ordering is then  iff
iff  for sufficiently
large
for sufficiently
large  .
.
 .
.  : free product of
: free product of  and
and  .
.
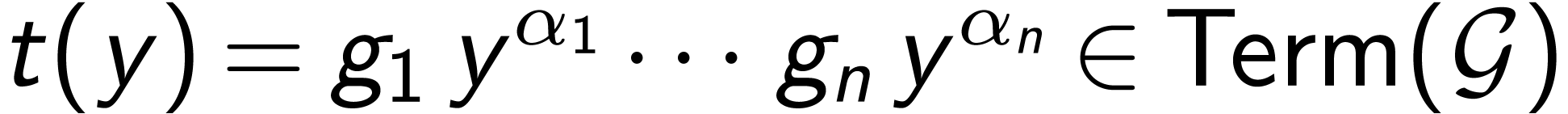
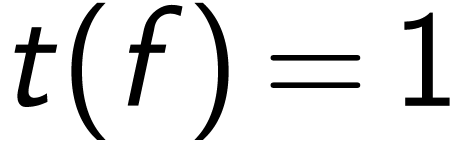 for
for  lying in extensions
of
lying in extensions
of 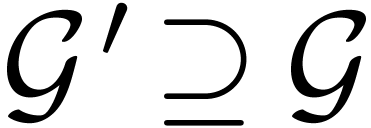 and
and  , the extension
, the extension  is determined by an ordering
on the quotient group
is determined by an ordering
on the quotient group  where
where
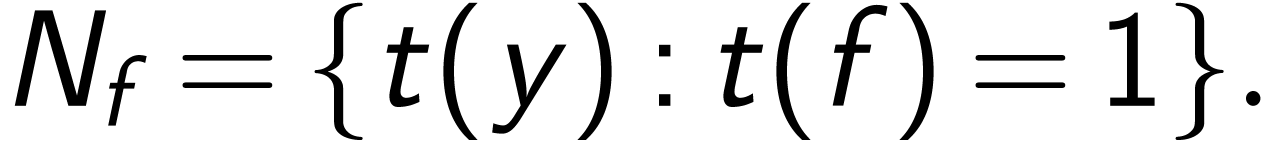
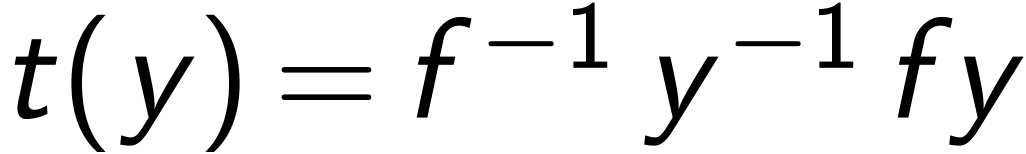
 centralizer
extension
centralizer
extension
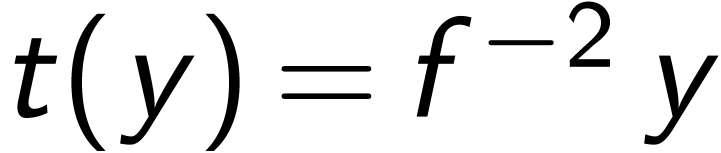

 is Abelian. For
is Abelian. For
 , we have
, we have 
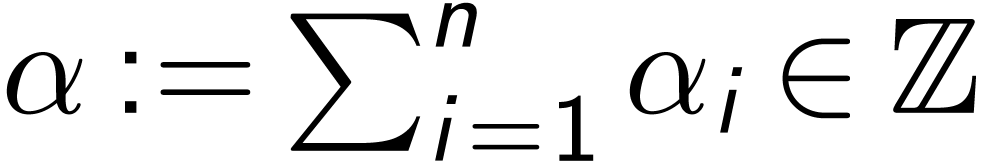 and
and  .
.
 .
.
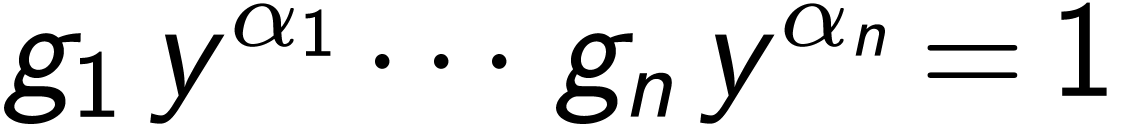
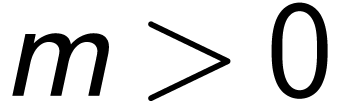 ,
, 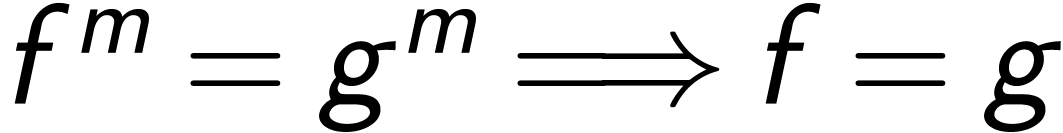 .
.
 ,
,
 .
.
 .
.
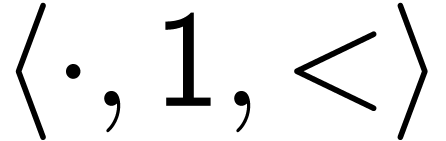 induces an elementary class in
induces an elementary class in 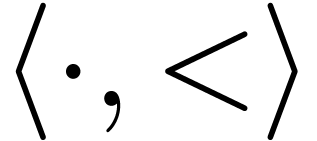 of thus orderable groups.
of thus orderable groups.
 and a convex normal subgroup
and a convex normal subgroup  such that
such that 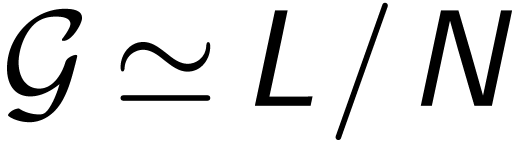 .
.
 be an o-minimal
structure.
be an o-minimal
structure.
 for the set of
germs
for the set of
germs  at
at  of definable maps
of definable maps 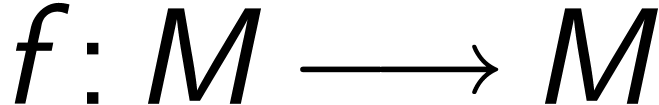 . We have
. We have 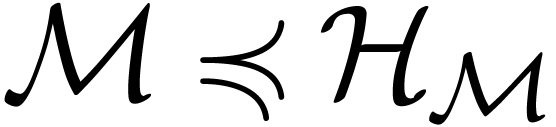 for a natural “asymptotic” structure on
for a natural “asymptotic” structure on 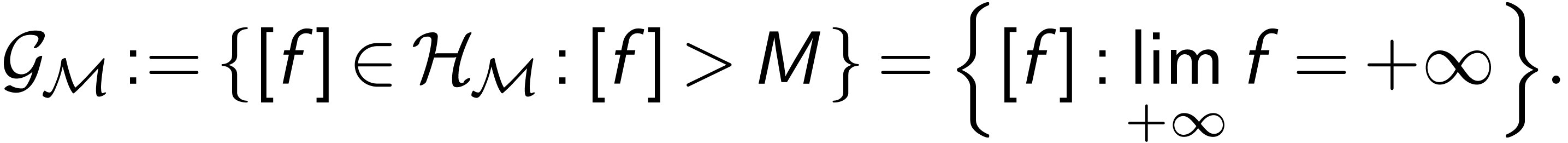
 is closed under
composition
is closed under
composition  , and
, and  is an ordered group.
is an ordered group.
 :
real-closed field.
:
real-closed field. 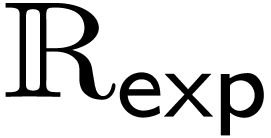 :
real exponential field.
:
real exponential field.
 , we have
, we have 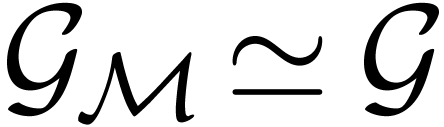 .
.
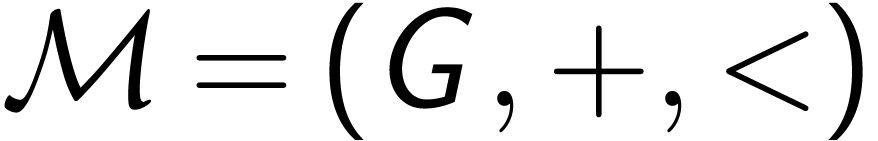 is a divisible
ordered Abelian group, then
is a divisible
ordered Abelian group, then  .
.
 , we have
, we have  . Moreover
. Moreover  . Moreover
. Moreover 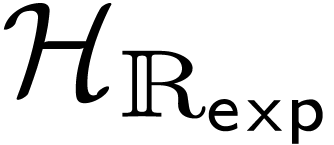 contains
all germs of functions that can be obtained as combinations of
contains
all germs of functions that can be obtained as combinations of
 ,
,  , and semialgebraic functions.
, and semialgebraic functions.
 with
with
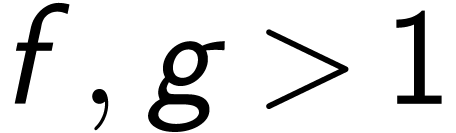 . How is the
inequation
. How is the
inequation

 , if
, if  , then
, then 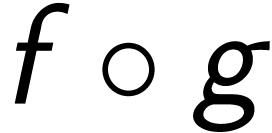 intuitively grows faster than
intuitively grows faster than  .
.
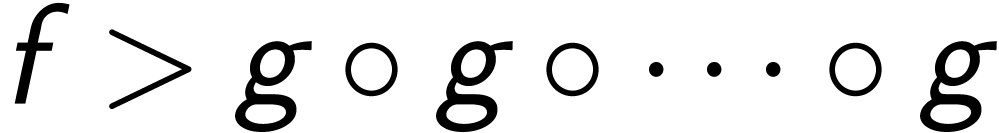 for all finite iterations.
for all finite iterations.
 ,
where
,
where
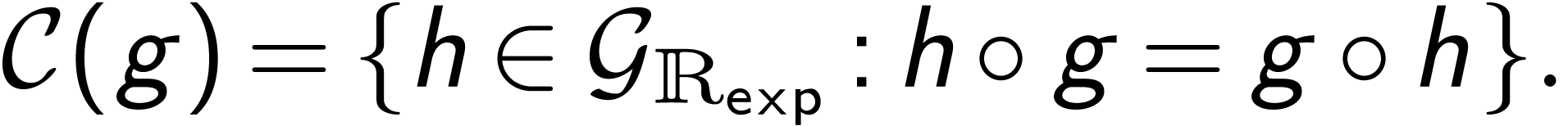
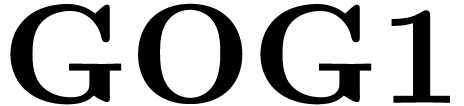
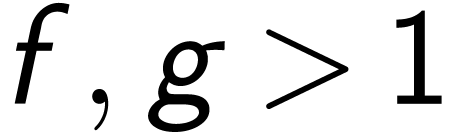 ,
we have
,
we have  .
.
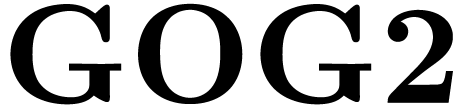
 and all
and all 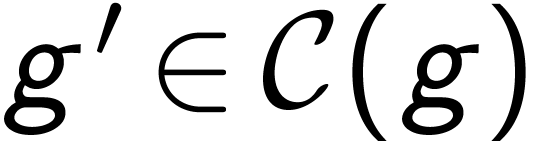 , there is an
, there is an 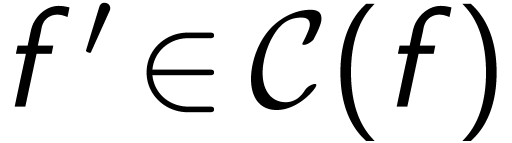 with
with  .
.
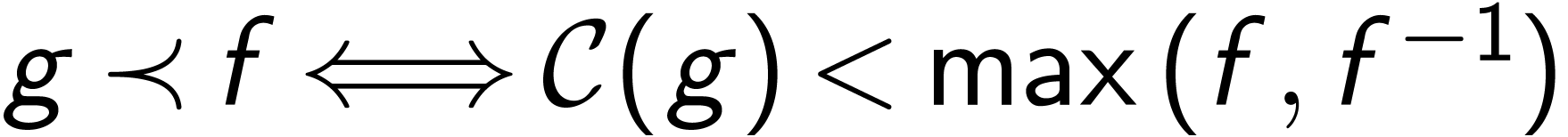 is an ordering which is compatible with
is an ordering which is compatible with  . The relation
. The relation  if (
if ( and
and  ) is a convex equivalence relation.
) is a convex equivalence relation.
 is said
central if for all
is said
central if for all  ,
there is a
,
there is a 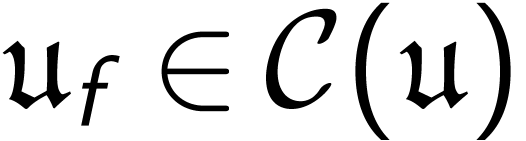 such that
such that
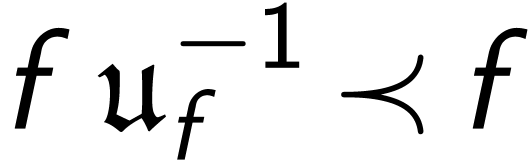 .
.
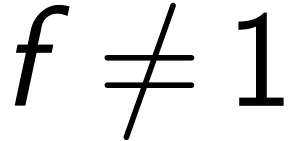 ,
there is a central
,
there is a central 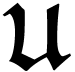 with
with  .
.
 expands the real ordered field, then must
expands the real ordered field, then must 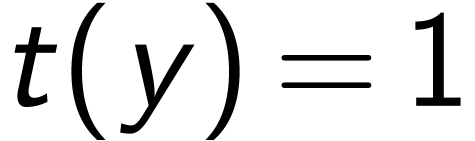 by constructing ordered
differential fields of formal series with composition laws:
by constructing ordered
differential fields of formal series with composition laws:
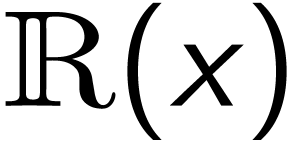 with
with 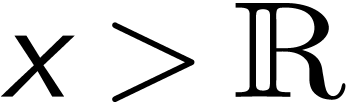 . For
. For  with
with  , the derivative
, the derivative
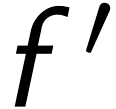 and the compositum
and the compositum  of formal Laurent series.
of formal Laurent series.
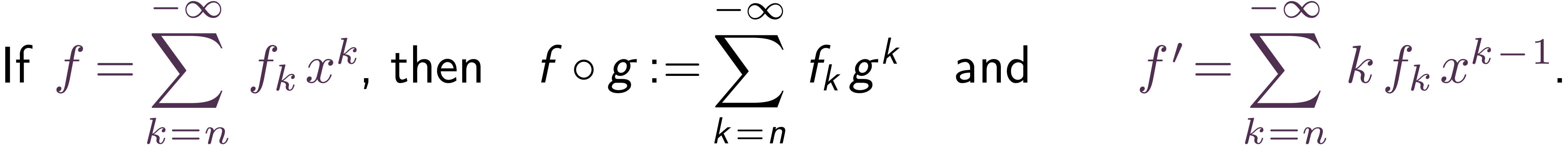
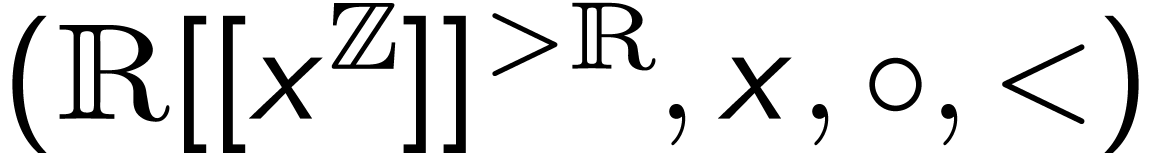 is not a group.
is not a group. 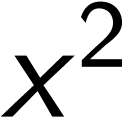 has no inverse
has no inverse
 of Puiseux series, and
of Puiseux series, and 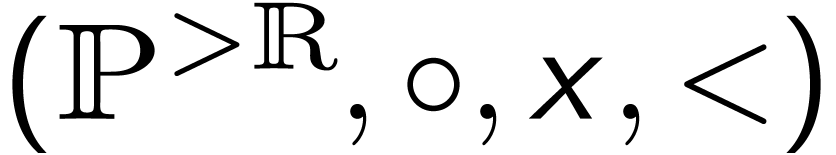 is a growth order group.
is a growth order group.
 conjugate in
conjugate in  ?
?
 and
and  are not conjugate.
are not conjugate.
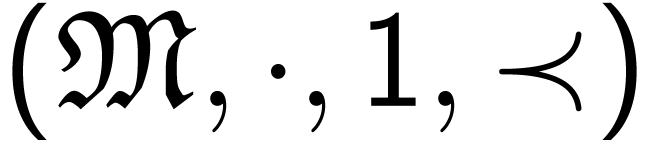 be a linearly
ordered abelian group. Then
be a linearly
ordered abelian group. Then 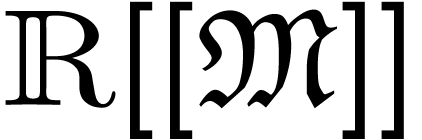 is an ordered field for the Cauchy product
is an ordered field for the Cauchy product
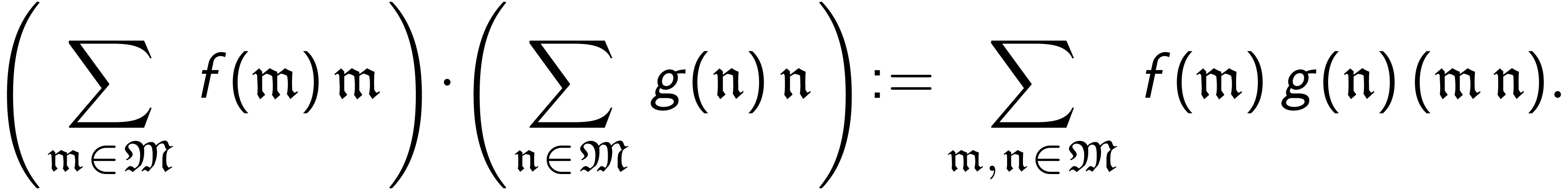
 is infinitesimal
then
is infinitesimal
then  .
.
 of
transseries: generalized series involving
of
transseries: generalized series involving  ,
,  and
and 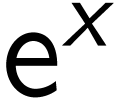 and combinations
thereof.
and combinations
thereof.

 and
and  must be
uniformly bounded.
must be
uniformly bounded.
 enjoys a
derivation
enjoys a
derivation 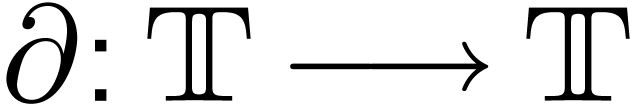 that acts termwise, e.g.
that acts termwise, e.g.
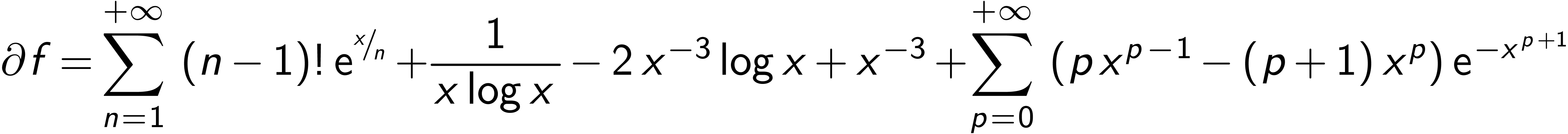
 enjoys a
composition law
enjoys a
composition law 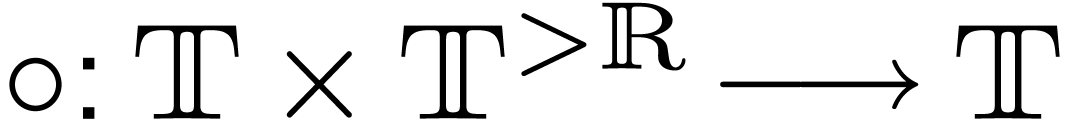 that acts termwise on the right:
that acts termwise on the right:
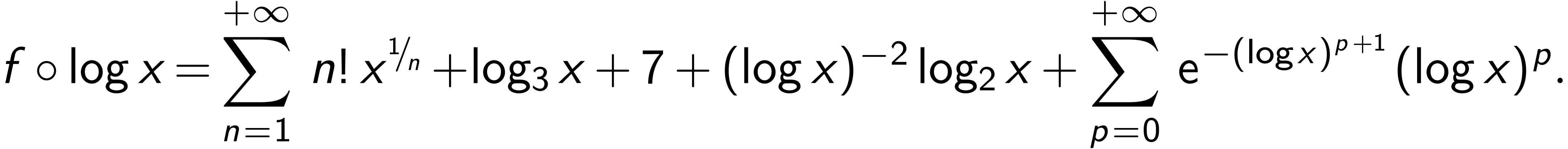
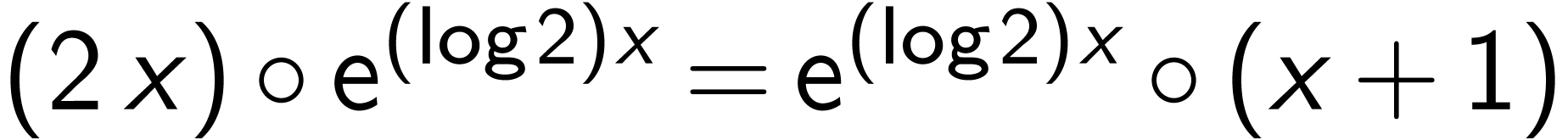 .
.
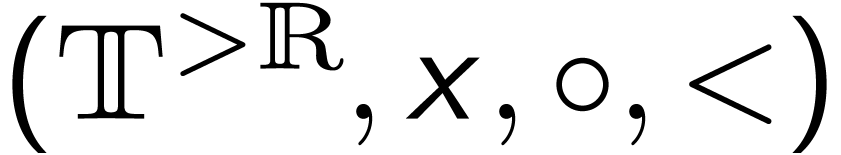 .
.
 ,
,  .
.
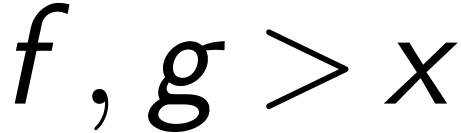 with
with
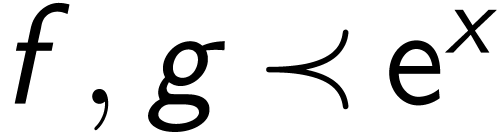 are conjugate.
are conjugate.
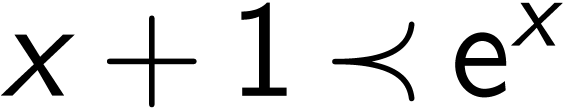 and
and 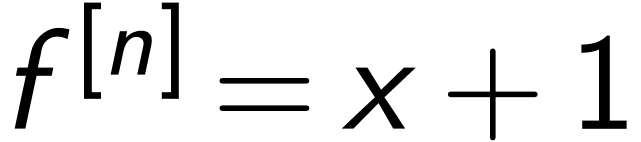 has a solution
has a solution  for all
for all  ,
we deduce that
,
we deduce that

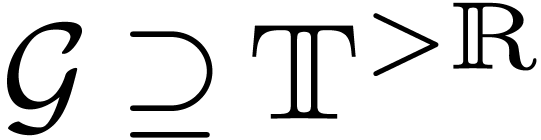 in which
in which  solve the conjugacy equation
solve the conjugacy equation
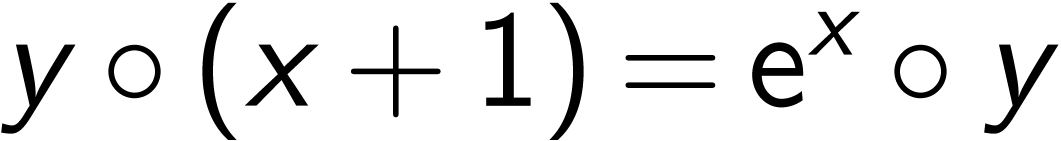
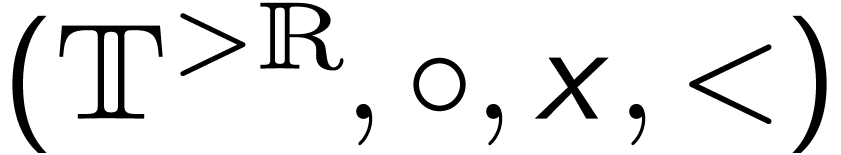 .
.
 of
of
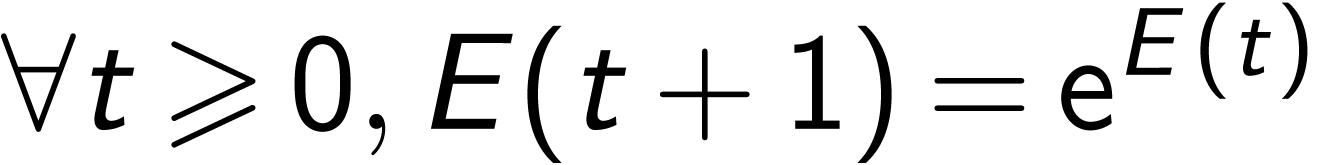
 . Its growth is
transexponential:
. Its growth is
transexponential: 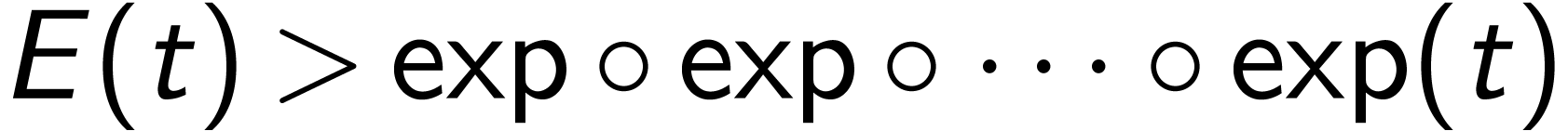 for
sufficiently large
for
sufficiently large  .
.
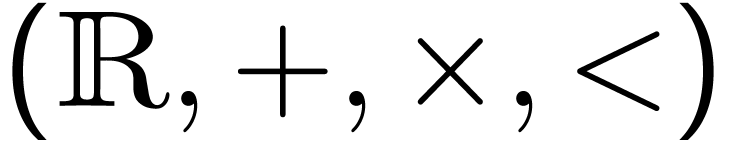 define a transexponential function?
define a transexponential function?
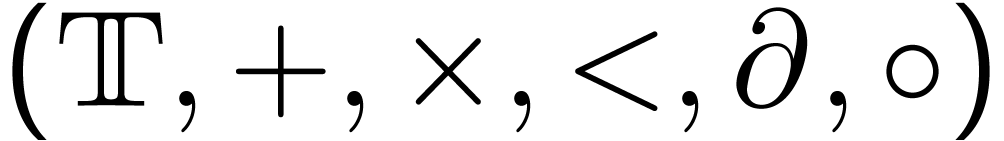 .
.
 with composition where (
with composition where (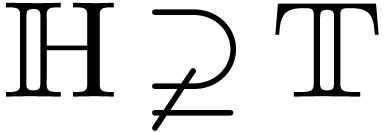 with formal
symbols
with formal
symbols  for all
for all 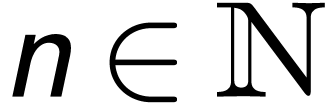 , where
, where 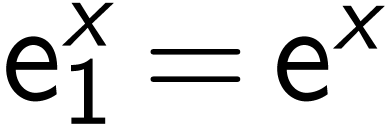 and
and
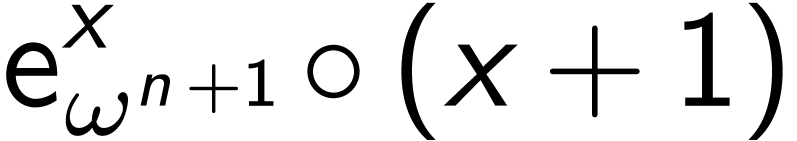
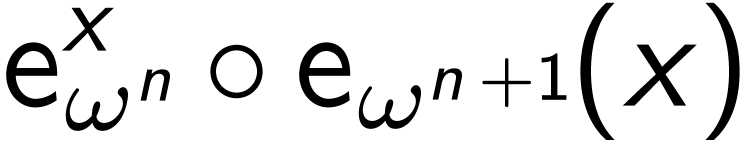
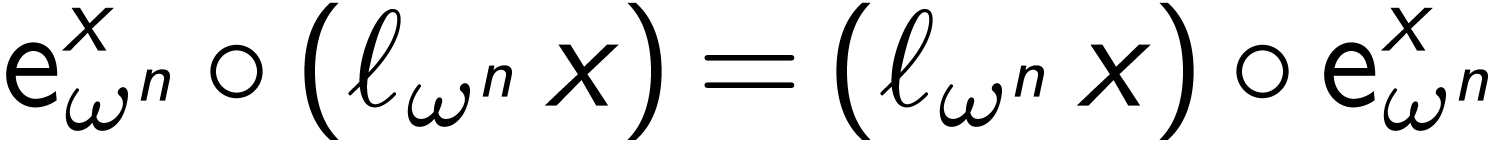

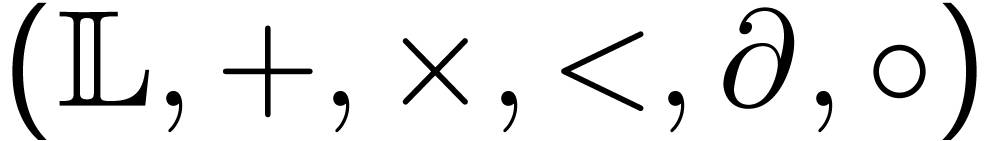 where for all
where for all 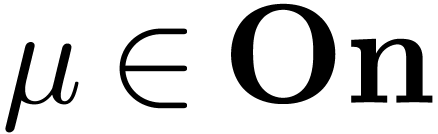 , we have a symbol
, we have a symbol  with
with  and
and
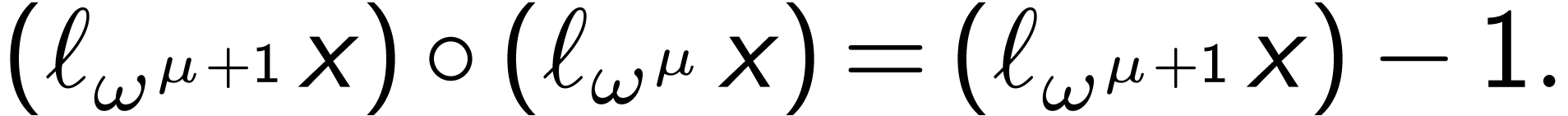
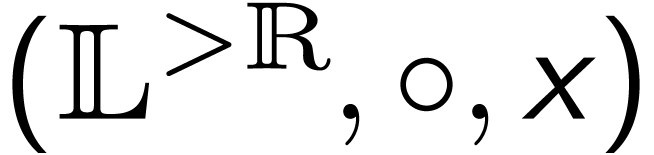 is not a group.
is not a group.
 where
where 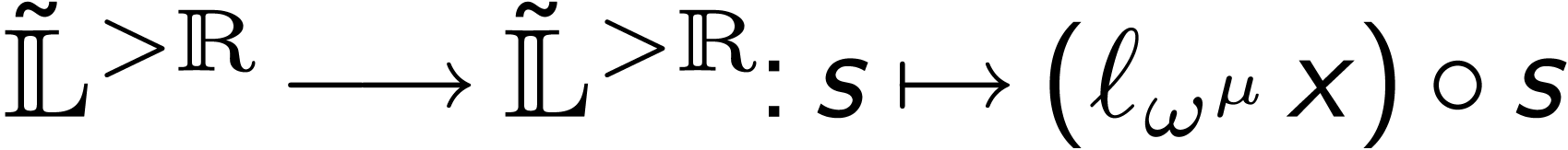 is bijective
and strictly increasing.
is bijective
and strictly increasing.
 and composition law
and composition law  on
on  extend in a
natural way to
extend in a
natural way to  .
.
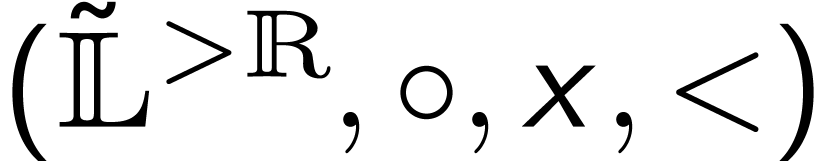 is
an ordered group.
is
an ordered group.
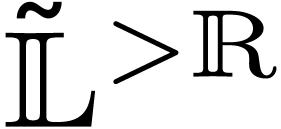 , all
conjugacy equations can now be solved:
, all
conjugacy equations can now be solved:
 in
in  of surreal
numbers. It comes with a linear ordering
of surreal
numbers. It comes with a linear ordering  of
simplicity.
of
simplicity.
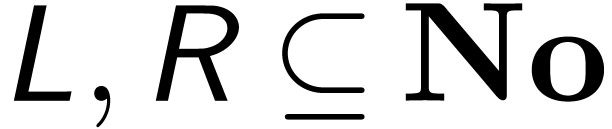 are subsets with
are subsets with  ,
then there is a unique
,
then there is a unique 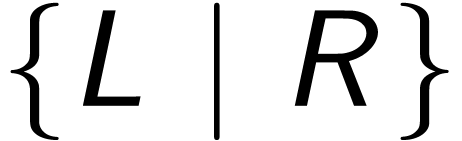 with
with  .
.
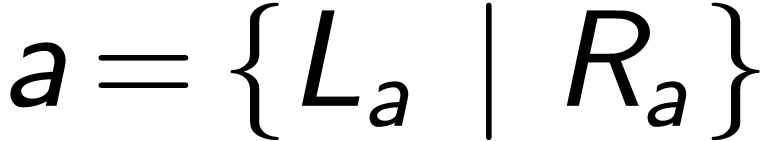 ,
,
 , we have
, we have
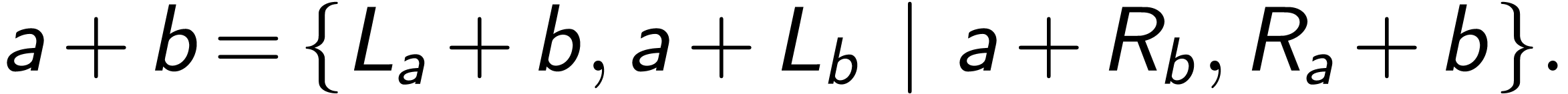
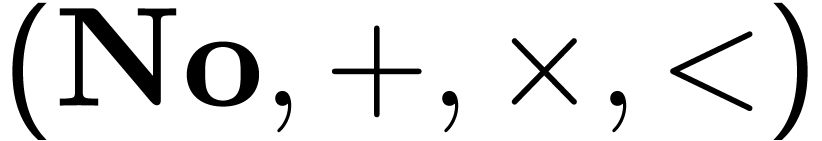 naturally contains the reals
naturally contains the reals  with their Hessenberg (commutative) arithmetic.
with their Hessenberg (commutative) arithmetic.
 corresponding to the ordinal
corresponding to the ordinal  .
.
 and
and  , define
, define  as the number
as the number

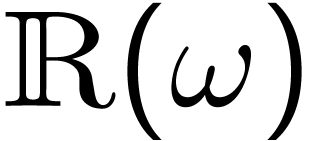 for polynomial asymptotics.
for polynomial asymptotics.
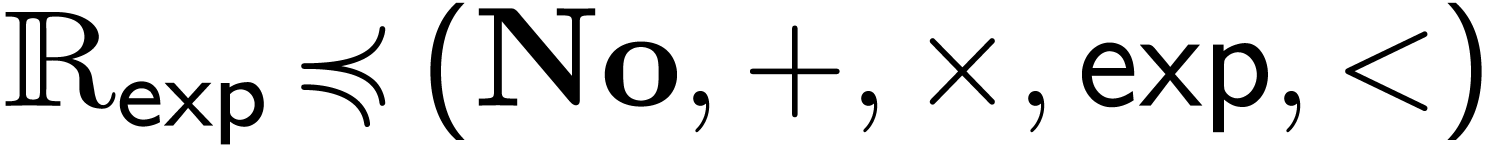 .
.
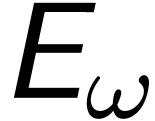 on
on 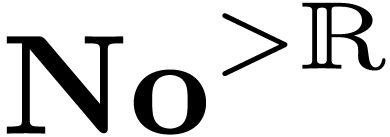 .
.
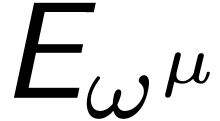 and
and 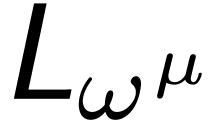 as in
as in 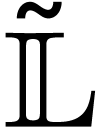 on surreal numbers.
on surreal numbers.
 , and every
surreal number can be represented as a (possibly infinitely
nested) hyperseries in the same vein as elements of
, and every
surreal number can be represented as a (possibly infinitely
nested) hyperseries in the same vein as elements of 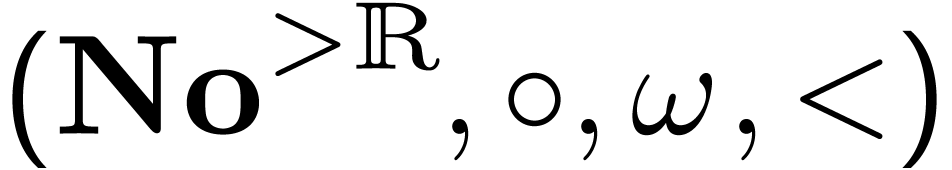 is a growth order
group with exactly three conjucacy classes.
is a growth order
group with exactly three conjucacy classes.
 ,
, 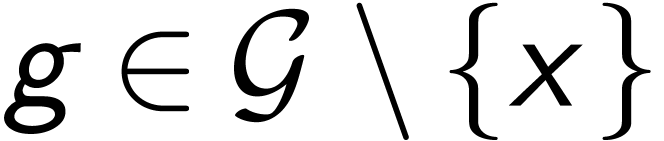 , we have a unique isomorphism
, we have a unique isomorphism

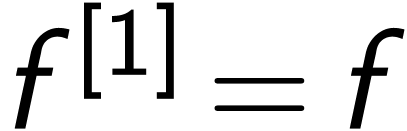 . Indeed this holds
for
. Indeed this holds
for 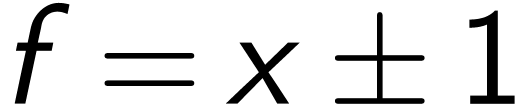 , and is carried over
by conjugacy.
, and is carried over
by conjugacy.
 operation, one
can define, for all strictly
operation, one
can define, for all strictly  -decreasing
ordinal indexed sequence
-decreasing
ordinal indexed sequence 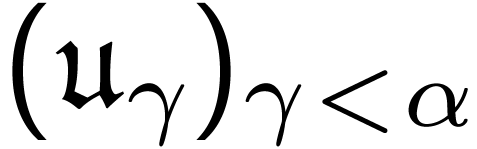 of “
of “ -simple”
elements of
-simple”
elements of  , a transfinite composition
, a transfinite composition
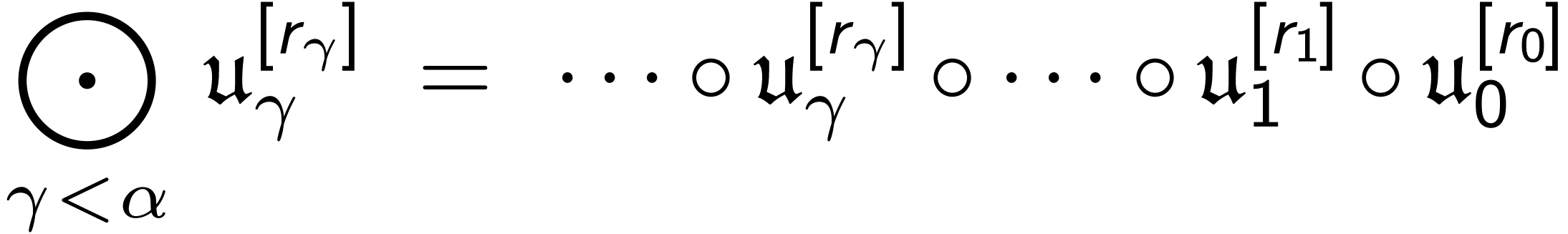
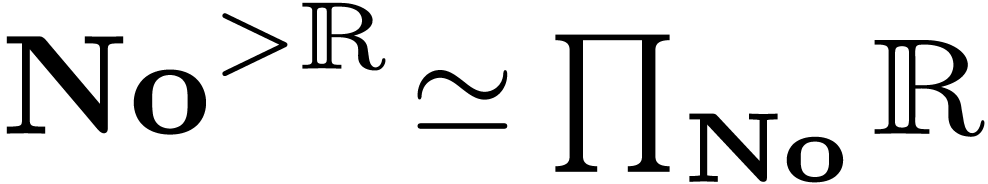 .
.
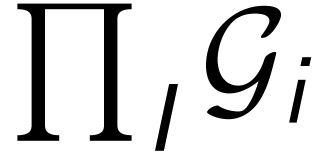 of Abelian ordered groups
of Abelian ordered groups 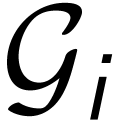 indexed by a linearly ordered set
indexed by a linearly ordered set  ?
?