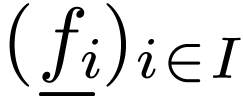 with arities
with arities 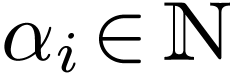 ,
together with of one of two types together with a family of relation
symbols
,
together with of one of two types together with a family of relation
symbols 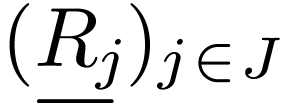 with arities
with arities 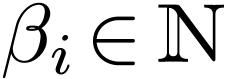 . Among the relation symbols, there is always a
particular symbol of arity
. Among the relation symbols, there is always a
particular symbol of arity 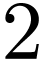 denoted
denoted  .
.
|
A signature is a family of function symbols
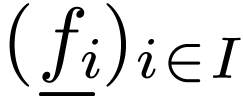 with arities
with arities 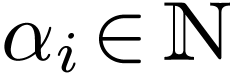 ,
together with of one of two types together with a family of relation
symbols
,
together with of one of two types together with a family of relation
symbols 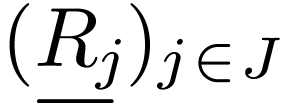 with arities
with arities 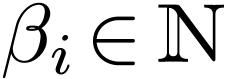 . Among the relation symbols, there is always a
particular symbol of arity
. Among the relation symbols, there is always a
particular symbol of arity 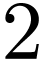 denoted
denoted  .
.
Given a signature 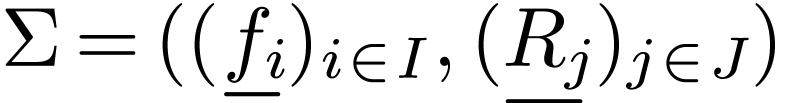 , a
first-order structure for
, a
first-order structure for  is
a set
is
a set 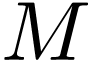 , together with a
family
, together with a
family 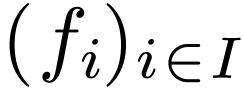 of functions
of functions 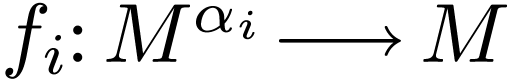 and
a family
and
a family 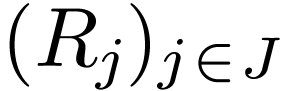 of subsets
of subsets 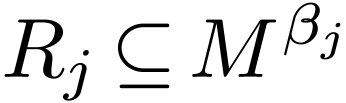 called relations. Each of these defines a specific interpretation of the
function and relation symbols. For instance a relation symbol
called relations. Each of these defines a specific interpretation of the
function and relation symbols. For instance a relation symbol  of arity
of arity  is interpreted by binary
relation
is interpreted by binary
relation 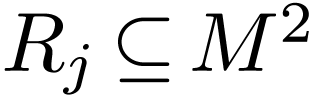 , a function
, a function 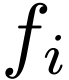 of arity 0 is interpreted as a constant
of arity 0 is interpreted as a constant 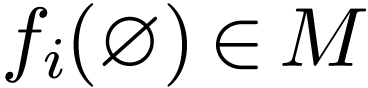 , a relation of arity
, a relation of arity 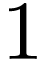 is interpreted subset of
is interpreted subset of 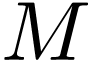 .
The equality symbol is always interpreted as the binary relation of
equality on
.
The equality symbol is always interpreted as the binary relation of
equality on 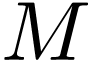 , i.e. as the
diagonal
, i.e. as the
diagonal 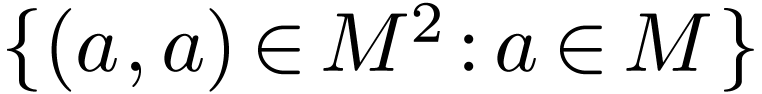 .
.
We will consider certain properties of 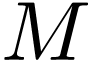 that
pertain to these functions and relations, and which can be stated in a
specific language involving symbols for each such function and relation.
This language is called a first-order language.
that
pertain to these functions and relations, and which can be stated in a
specific language involving symbols for each such function and relation.
This language is called a first-order language.
Example  , then we will take two functions
, then we will take two functions 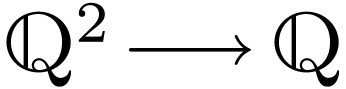 , namely the sum and the product, two constants
, namely the sum and the product, two constants
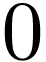 and
and 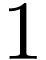 ,
and one binary relation, namely the standard ordering on
,
and one binary relation, namely the standard ordering on  , seen here as the subset
, seen here as the subset 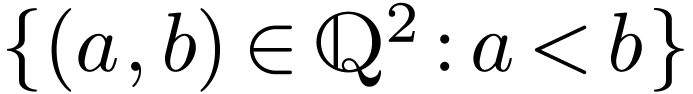 of
of 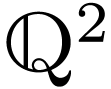 .
.
Example 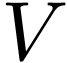 over
over
 , then we'll have the group
operation
, then we'll have the group
operation 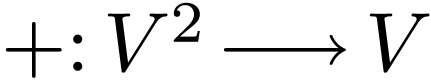 on
on 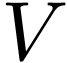 and, for
each complex number
and, for
each complex number 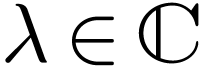 , the
scalar multiplication by
, the
scalar multiplication by 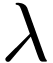 :
:
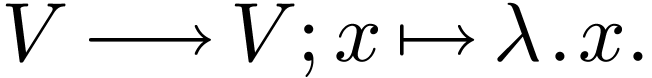
Consider a fixed signature 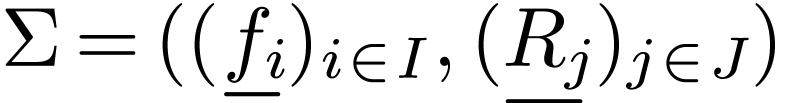 .
We then define specific types and sets of words, i.e. finite
strings of symbols, as follows:
.
We then define specific types and sets of words, i.e. finite
strings of symbols, as follows:
The set 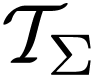 of terms
in the signature
of terms
in the signature 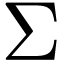 is the smallest set of
finite strings of symbols among variable symbols, parentheses
symbols ( and ) and function symbols
is the smallest set of
finite strings of symbols among variable symbols, parentheses
symbols ( and ) and function symbols 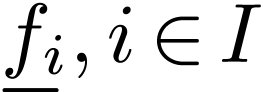 ,
which contains all variable symbols, and such that for all
,
which contains all variable symbols, and such that for all 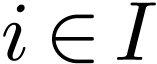 , if
, if 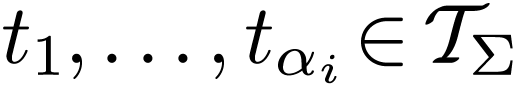 , then
, then 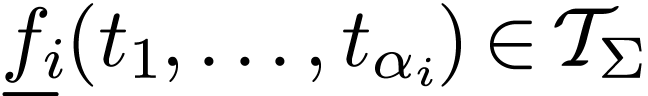 .
.
For instance, if 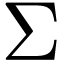 contains two function
symbols
contains two function
symbols 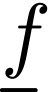 and
and 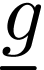 of
arities
of
arities 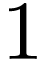 and
and 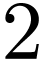 respectively, then the word
respectively, then the word
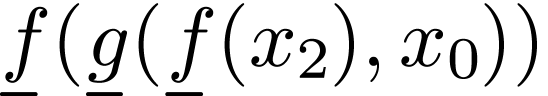
is a term.
Atomic formulas are words of the form
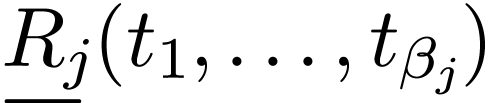 where
where 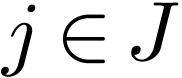 and
and  are terms and
are terms and 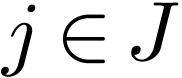 .
Neg-atomic formulas are words of the
form
.
Neg-atomic formulas are words of the
form 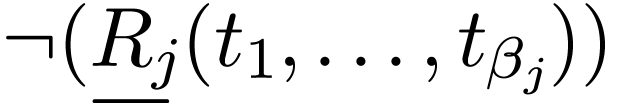 where
where 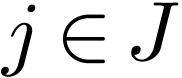 and
and  are terms and
are terms and 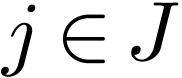 .
.
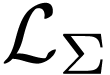 -formulas are well-written words involving atomic formulas,
parentheses, logical connectives
-formulas are well-written words involving atomic formulas,
parentheses, logical connectives 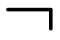 (“not”, negation),
(“not”, negation),  (“or”, disjunction),
(“or”, disjunction),  (“and”, conjunction), and quantifiers
(“and”, conjunction), and quantifiers 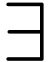 (“there exists”, existential quantifier), and
(“there exists”, existential quantifier), and  (“for all”, universal quantifier).
(“for all”, universal quantifier).
The first-order language 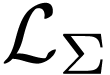 over this signature is the set of all
over this signature is the set of all 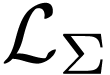 -formulas.
-formulas.
If a symbol of variable occuring in a formula is preceded by a
quantifier in one of its occurrences, then we say that it is bound.
Otherwise, we say that it is free. Usually, we write
denote by  an
an 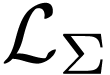 -formula
-formula 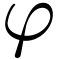 whose free
variables are among
whose free
variables are among  .
.
A formula without free variable is called an 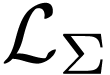 -sentence. Those are the formulas which can be
interpreted as true or false in structures (whereas formulas with free
variables may have a truth value depending on the value of those
variables).
-sentence. Those are the formulas which can be
interpreted as true or false in structures (whereas formulas with free
variables may have a truth value depending on the value of those
variables).
An 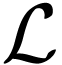 -formula is said
quantifier-free if it contains no occurrence of
-formula is said
quantifier-free if it contains no occurrence of 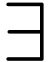 or
or  .
Quantifier-free formulas are thus boolean combinations of atomic
formulas, i.e. obtained as conjunctions, disjunctions and negations (and
combinations thereof) of atomic formulas.
.
Quantifier-free formulas are thus boolean combinations of atomic
formulas, i.e. obtained as conjunctions, disjunctions and negations (and
combinations thereof) of atomic formulas.
Proposition  is is logically
equivalent to a formula of the form
is is logically
equivalent to a formula of the form
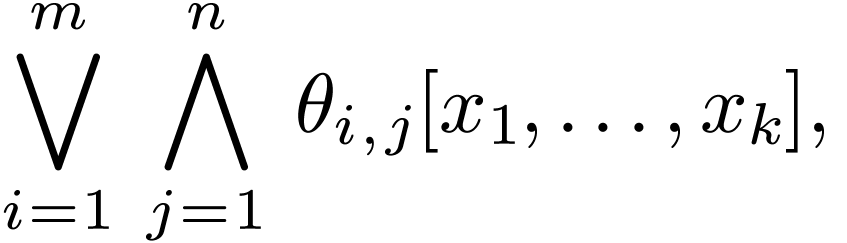
where 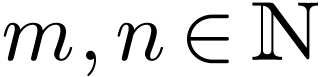 , and each
, and each 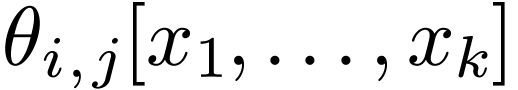 is either atomic or neg-atomic.
is either atomic or neg-atomic.
An  -formula is in prenex
normal form form if it is, up to permutation of the
variable symbols, of the form
-formula is in prenex
normal form form if it is, up to permutation of the
variable symbols, of the form

where  is quantifier-free and
is quantifier-free and  are symbols of quantifiers (i.e.
are symbols of quantifiers (i.e. 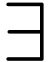 or
or  ).
).
Proposition 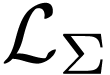 -formula is logically equivalent to
a formula in prenex normal form.
-formula is logically equivalent to
a formula in prenex normal form.
We fix a signature 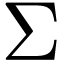 and an
and an 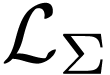 -structure
-structure 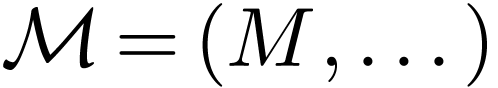 .
Given a formula
.
Given a formula  and
and 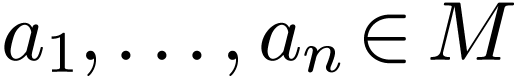 , we say that
, we say that  holds in
holds in  if the
straightforward interpretation of
if the
straightforward interpretation of  ,
where
,
where
each variable symbol 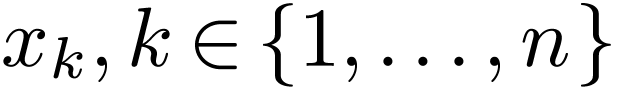 is replaced by
is replaced by 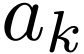 ,
,
each function symbol 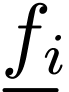 is replaced by the
function
is replaced by the
function 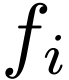 ,
,
each term  is replaced by the element
is replaced by the element 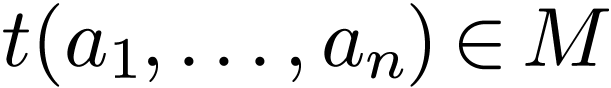 accordingly,
accordingly,
each atomic formula 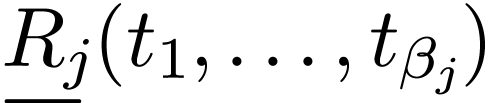 is replaced by the
statement:
is replaced by the
statement:
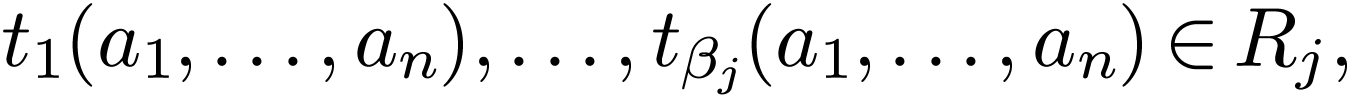
each logical combination thereof is evaluated following basic logic,
is true.
Remark  only apply
to variables which range in elements, and not subsets of the structure.
One could also have symbols of variable
only apply
to variables which range in elements, and not subsets of the structure.
One could also have symbols of variable 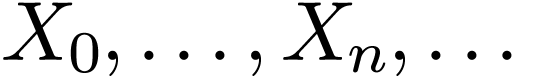 denoting
subsets of
denoting
subsets of  , so that a
formula in this higher-order language for the structure
, so that a
formula in this higher-order language for the structure 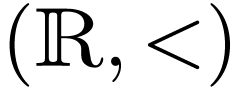 could state that
could state that 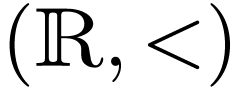 has the least upper bound
property.
has the least upper bound
property.
But the first-order language does not allow this. It can be shown that
there is no set 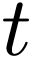 of sentences in the first-order
language over
of sentences in the first-order
language over 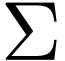 with one binary relation symbol
such that
with one binary relation symbol
such that 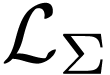 -structure in which
all sentences in
-structure in which
all sentences in 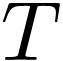 hold are exactly linearly
ordered sets with the least upper bound property.
hold are exactly linearly
ordered sets with the least upper bound property.
Consider a first-order signature 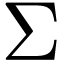 and an
and an 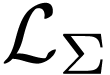 -structure
-structure  . We say that
. We say that  eliminates
quantifiers (or has quantifier elimination) if for every
eliminates
quantifiers (or has quantifier elimination) if for every
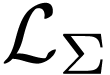 -formula
-formula  , there is a quantifier-free
, there is a quantifier-free 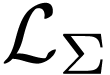 -formula
-formula  such that the
following sentence holds in
such that the
following sentence holds in  :
:
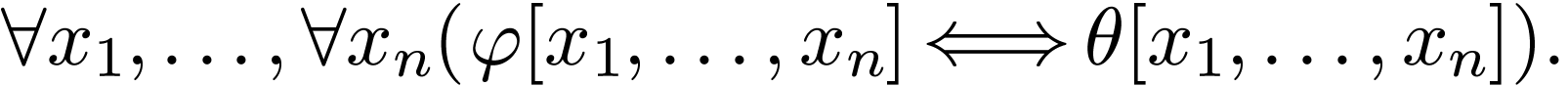
There are many tests in order to show that  eliminates quantifiers. One of the most basic ones is the following
eliminates quantifiers. One of the most basic ones is the following
Proposition  and each quantifier-free formula
and each quantifier-free formula 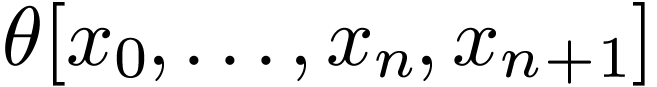 , there is a quantifier-free
formula
, there is a quantifier-free
formula  such that the following holds in
such that the following holds in  :
:
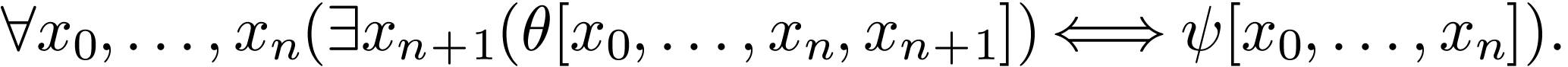
Then  eliminates quantifiers.
eliminates quantifiers.
Idea of proof. Prenex normal form  induction.
induction.
In this section, we fix a first-order signature 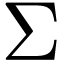 and an
and an  -structure
-structure 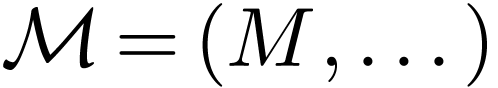 .
.
Given 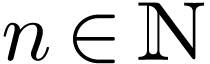 , we say that a set
, we say that a set
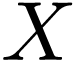 is definable in dimension
is definable in dimension
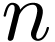 in
in  if
if 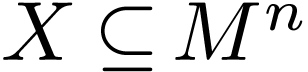 and there are an
and there are an 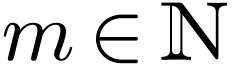 , a tuple
, a tuple
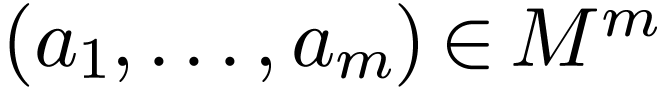 and a formula
and a formula 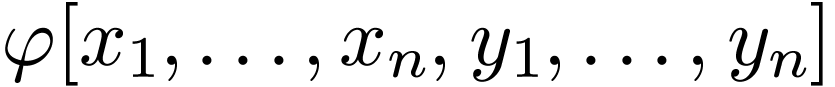 such that
such that
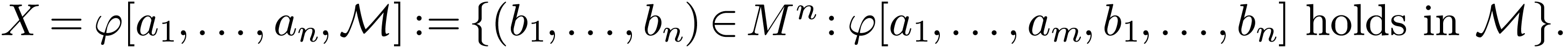
We say that 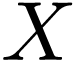 is definable without quantifiers if
is definable without quantifiers if
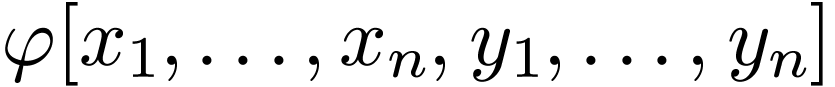 can be taken to be quantifier-free.
can be taken to be quantifier-free.
Example 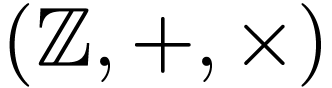 , the set
, the set 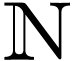 is definable. Indeed, Lagrange's four squares theorem, an integer
is definable. Indeed, Lagrange's four squares theorem, an integer 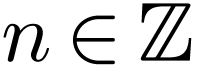 is positive if and only if it is a sum of for squares
of integers. So
is positive if and only if it is a sum of for squares
of integers. So
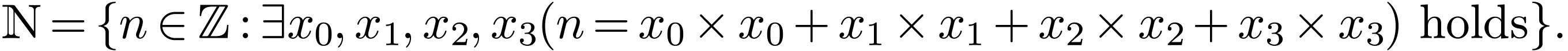
The set 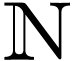 is not definable without
quantifiers. Indeed, recall that quantifier-free formulas are equivalent
to boolean combinations of atomic formulas. In
is not definable without
quantifiers. Indeed, recall that quantifier-free formulas are equivalent
to boolean combinations of atomic formulas. In 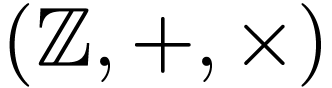 , an atomic formula in one free variable
, an atomic formula in one free variable 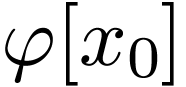 is equivalent to an equality
is equivalent to an equality 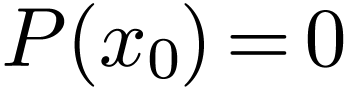 where
where
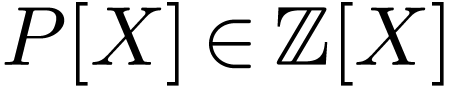 . Hence it defines either
. Hence it defines either
 if
if 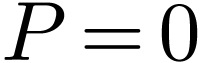 ,
or a finite subset otherwise. In particular, it defines a finite or
cofinite (complement of a finite) subset of
,
or a finite subset otherwise. In particular, it defines a finite or
cofinite (complement of a finite) subset of  . Since the set of finite or cofinite subsets of
. Since the set of finite or cofinite subsets of
 is closed under unions and intersections, any
boolean combination ot atomic formulas defines a finite or cofinite
subset. So
is closed under unions and intersections, any
boolean combination ot atomic formulas defines a finite or cofinite
subset. So 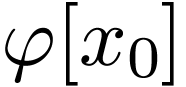 defines a finite or cofinite subset.
Since
defines a finite or cofinite subset.
Since 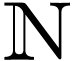 is neither finite nor cofinite in
is neither finite nor cofinite in  , it cannot be defined by
, it cannot be defined by 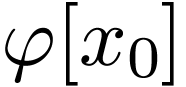 .
.
Remark 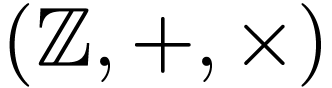 , many things are definable.
For instance, every recursively enumerable subset of
, many things are definable.
For instance, every recursively enumerable subset of 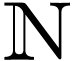 is definable in dimension
is definable in dimension 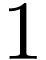 in
in 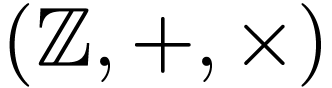 .
.
Here we fix an 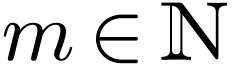 , an
, an 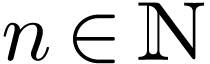 with
with 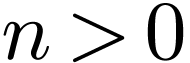 , a tuple
, a tuple
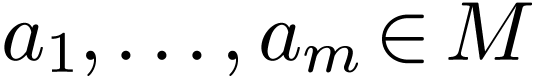 , as well as
, as well as 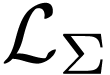 -formulas
-formulas
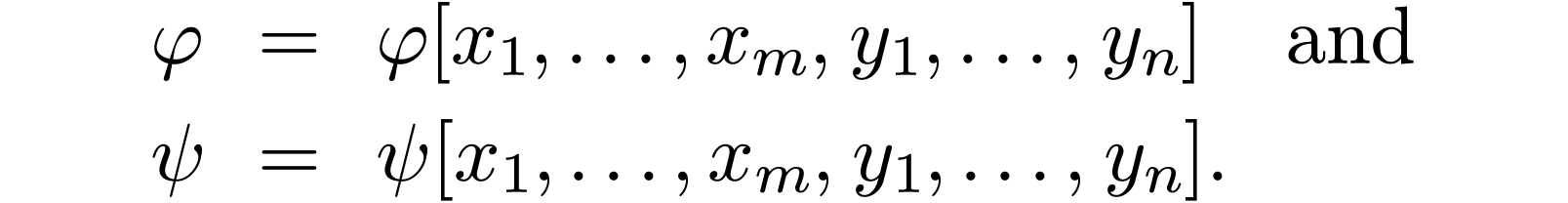
We have the following list of correspondences between geometric operations on definable sets
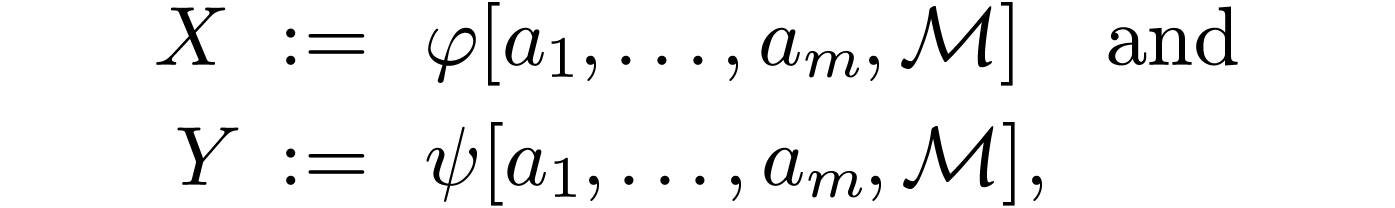
and their defining formulas 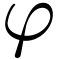 and
and 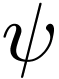 .
.
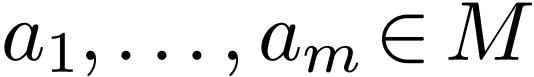
| Logical operation on defining formula | Geometric operation on definable set |
Negation 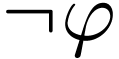 |
Complement 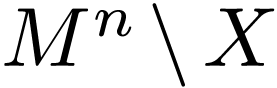 |
Disjunction:  |
Union  |
Conjunction:  |
Intersection  |
Existential quantifier: 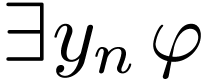 |
Projection on 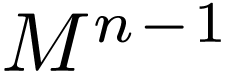 . . |
Universal quantifier: 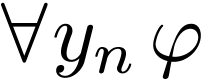 |
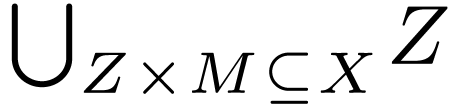 |
Thus the theory of definability can be stated in purely geometric terms. This is the spirit of [2]. However, many important results regarding definability (in particular in o-minimality) crucially rely on the interplay between intuitions coming from logic and geometry, algebra, analysis, graph theory, and so on...
Let 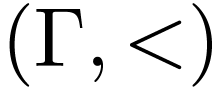 be a linearly ordered set. An
interval in
be a linearly ordered set. An
interval in 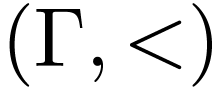 is a subset
is a subset 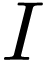 of one of the following forms for
of one of the following forms for 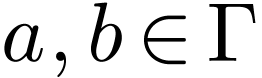 :
:
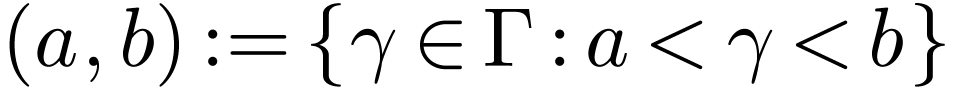 ,
,
 ,
,
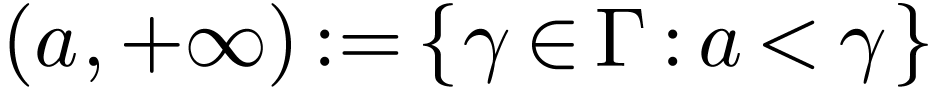 ,
,
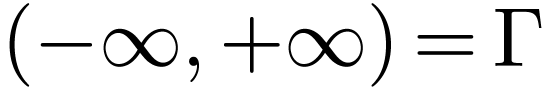 ,
,
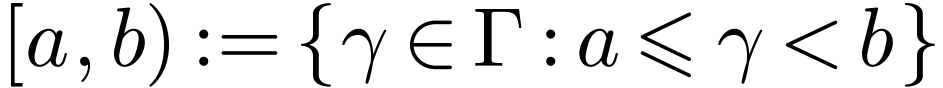 ,
,
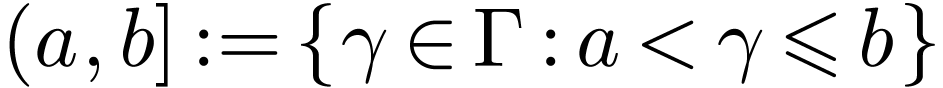 ,
,
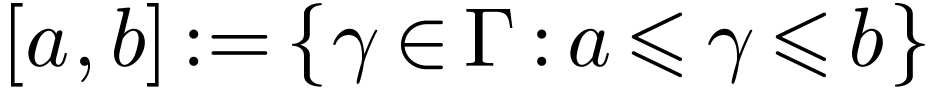 ,
,
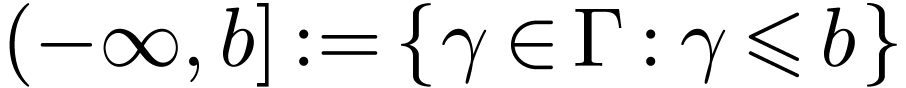 ,
,
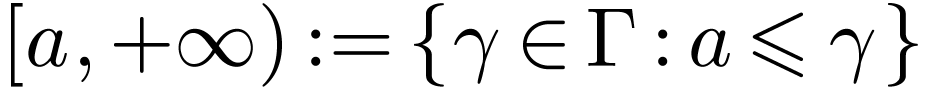 ,
,
The first four types of intervals are called open intervals.
Example 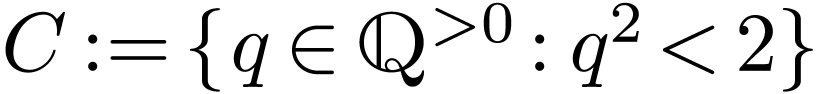 is not an interval in
is not an interval in 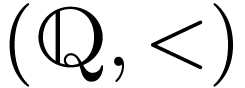 , whereas
, whereas
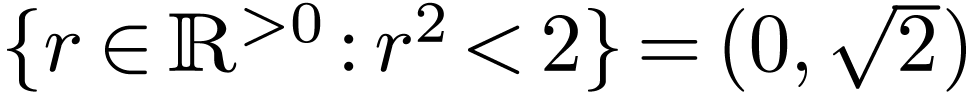
is an interval in 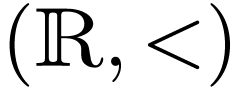 .
.
Proposition 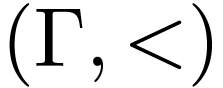 be a linearly ordered set. Then the quantifier-free
definable subsets of
be a linearly ordered set. Then the quantifier-free
definable subsets of 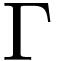 are exactly the finite
unions of intervals in
are exactly the finite
unions of intervals in 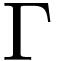 .
.
Definition 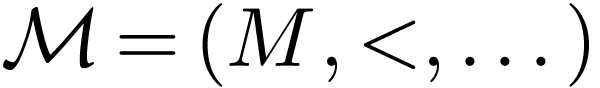 is said
o-minimal if every definable subset
of
is said
o-minimal if every definable subset
of  in dimension
in dimension 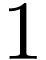 is a
finite union of intervals in
is a
finite union of intervals in 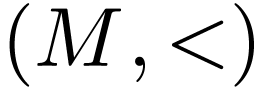 .
.
Corollary 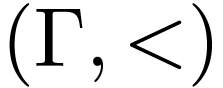 eliminates quantifiers, then it is o-minimal.
eliminates quantifiers, then it is o-minimal.
The set  in Example 9 is definable
in the ordered group
in Example 9 is definable
in the ordered group 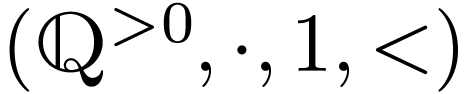 . This
set is not a finite union of intervals, otherwise it would have a least
upper bound in
. This
set is not a finite union of intervals, otherwise it would have a least
upper bound in  . Therefore
. Therefore
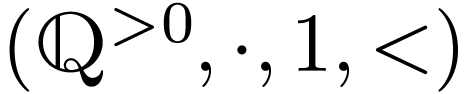 is not o-minimal.
is not o-minimal.
O-minimal ordered fields. In the Fachseminar and in RAG
I, we will see examples of o-minimal ordered fields. Here we consider
the case of rational numbers. The ordered field 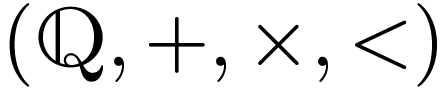 is not o-minimal for similar reasons as above. What's more, by a theorem
of Julia
is not o-minimal for similar reasons as above. What's more, by a theorem
of Julia  of integers is definable in
of integers is definable in 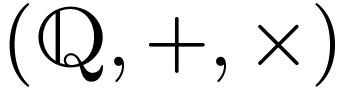 .
So every definable set in
.
So every definable set in 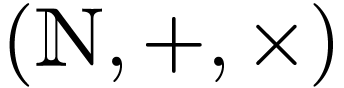 is definable in
is definable in 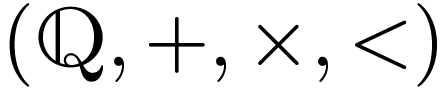 . In view of Remark 8,
we see that
. In view of Remark 8,
we see that 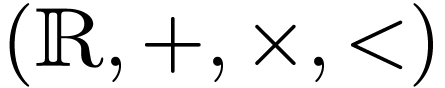 and
and 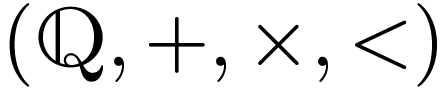 are at
the opposite ends of the spectrum of “tameness” of definable
subsets.
are at
the opposite ends of the spectrum of “tameness” of definable
subsets.
Proposition 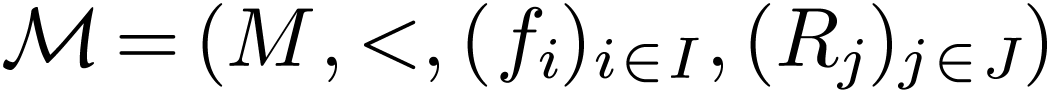 is o-minimal, and let
is o-minimal, and let 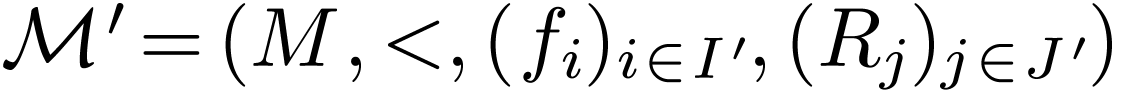 where
where 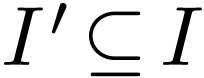 and
and 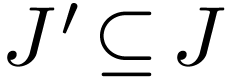 ,
as a first-oder structure in the language
,
as a first-oder structure in the language 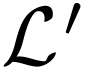 with
signature
with
signature 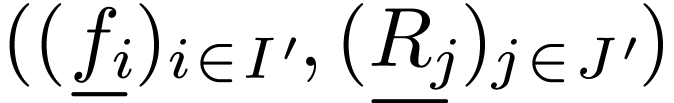 . Then
. Then 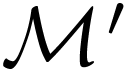 is o-minimal.
is o-minimal.
Proof.  -formulas
are
-formulas
are  -formulas, and given an
-formulas, and given an
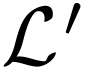 -formula
-formula 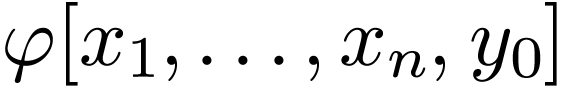 and
and 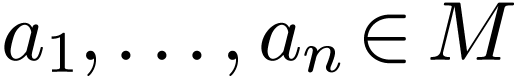 , the definable set
, the definable set 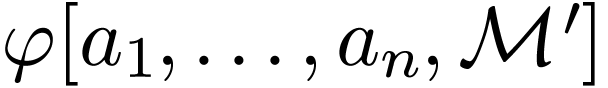 is equal to
is equal to 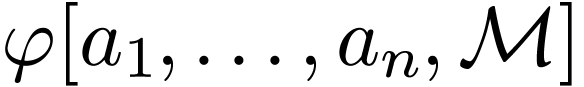 ,
which is a finite union of intervals by o-minimality of
,
which is a finite union of intervals by o-minimality of  , hence the result.
, hence the result.
Let 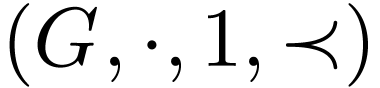 be a bi-ordered group. A unary
representation of
be a bi-ordered group. A unary
representation of  is a total
order
is a total
order 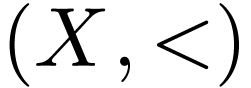 together with a morphism
together with a morphism
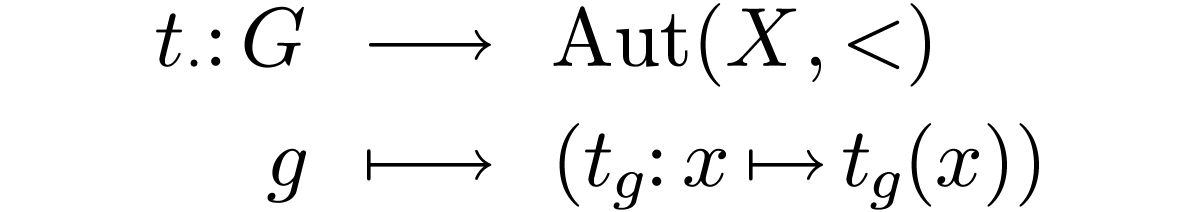
where 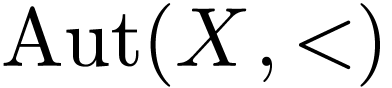 is the group under composition of strictly
increasing bijections
is the group under composition of strictly
increasing bijections  , such
that for all
, such
that for all 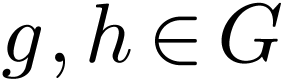 , we have
, we have
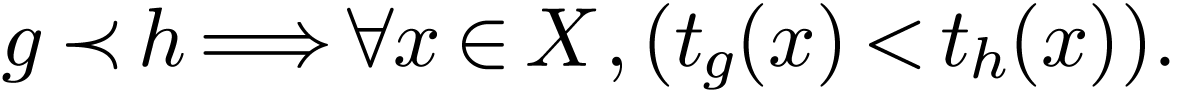
Example
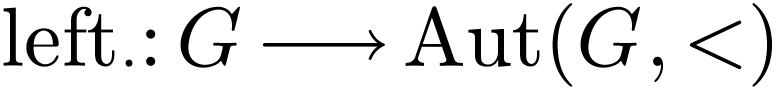
of  by letting it act on itself by left
translations, i.e. by setting
by letting it act on itself by left
translations, i.e. by setting 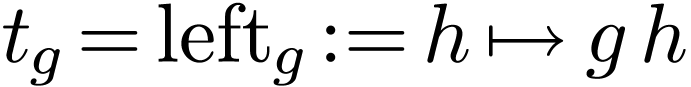 for
each
for
each 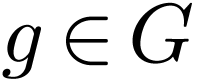 .
.
Example 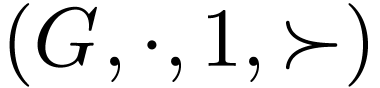 with the reverse ordering
with the reverse ordering  defined by
defined by

This is still a bi-ordered group. We have a unary representation

of  on its underlying linear ordering
on its underlying linear ordering 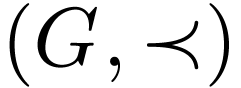 given by right translations:
given by right translations: 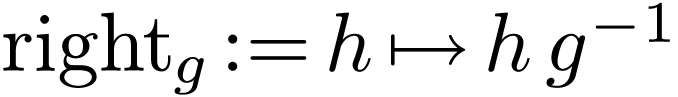 for
each
for
each 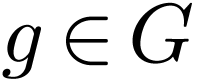 .
.
We now fix a unary representation 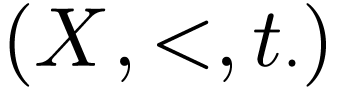 of
of 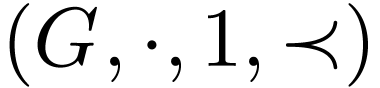 , and we consider the first-order
structure
, and we consider the first-order
structure 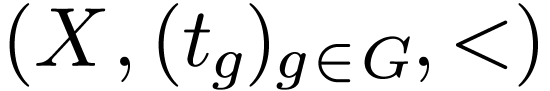 in the first-order language
in the first-order language 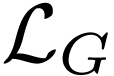 with unary function symbols
with unary function symbols 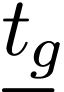 for
each
for
each 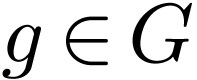 and a binary relation symbol
and a binary relation symbol 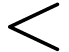 . We then have
. We then have
Theorem 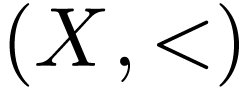 is dense or that
is dense or that 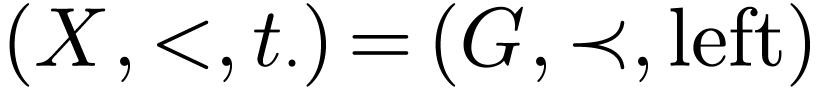 .
Then
.
Then 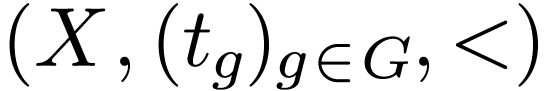 has quantifier elimination in
has quantifier elimination in 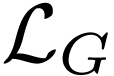 .
.
Proof. We first note that we have the following
equivalences for 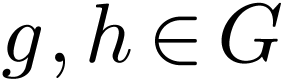 and
and 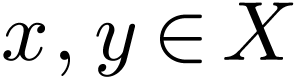 :
:
Now consider an existential formula 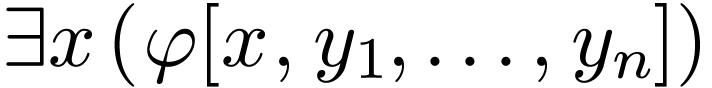 for
for 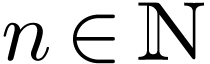 . So there are atomic and
neg-atomic formulas
. So there are atomic and
neg-atomic formulas 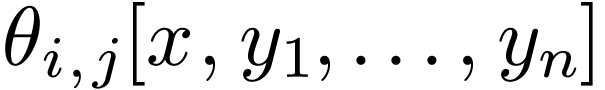 such that
such that
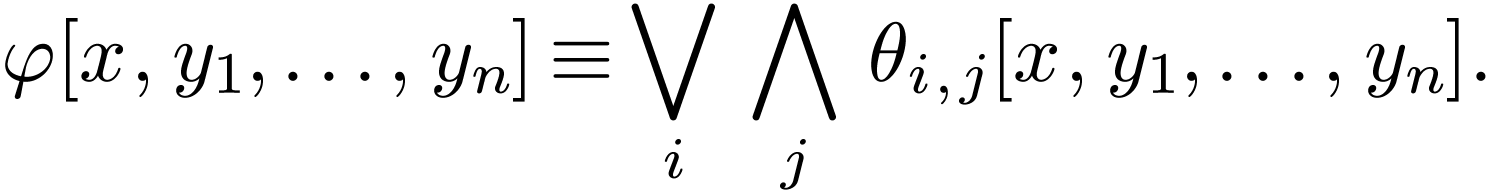
Each neg-atomic formula among the 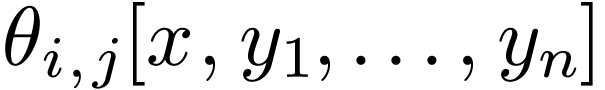 's
may be replaced by a disjunction of atomic formulas as in (3-4). Then as in (1-2), we may replace
all atomic formulas by formulas of the form
's
may be replaced by a disjunction of atomic formulas as in (3-4). Then as in (1-2), we may replace
all atomic formulas by formulas of the form 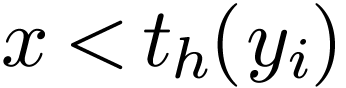 or
or
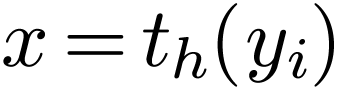 for
for 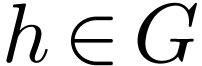 and
and 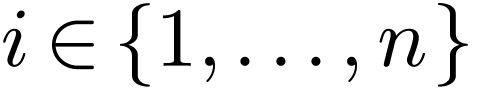 . So each
. So each 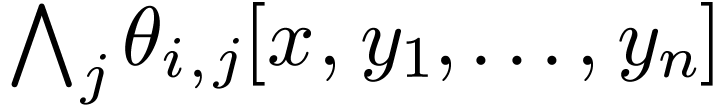 is equivalent
to a formula
is equivalent
to a formula
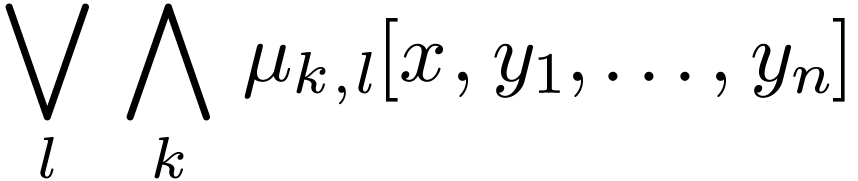
where each 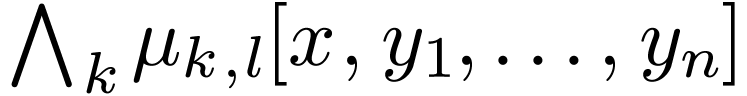 says that
says that
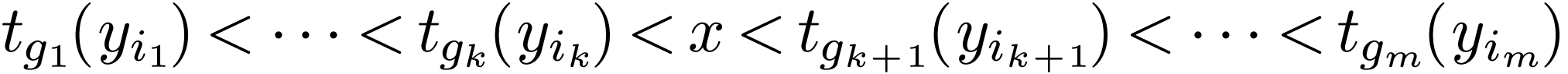
for some 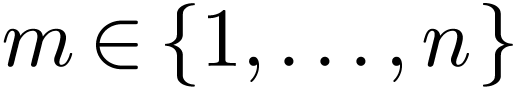 ,
, 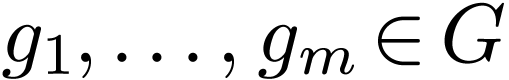 and
and 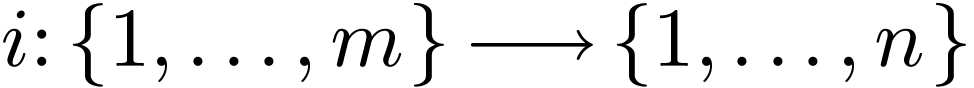 . Note that the formula
. Note that the formula
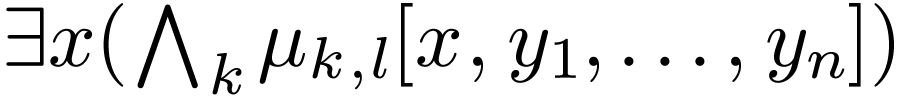 is false (hence equivalent to a quantifer-free
formula) if
is false (hence equivalent to a quantifer-free
formula) if 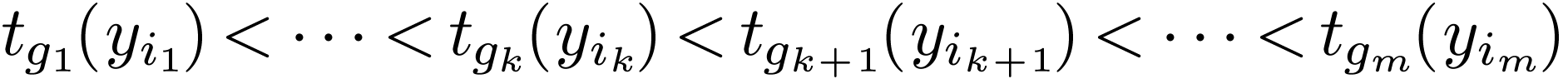 is false. If this last formula is
true, then
is false. If this last formula is
true, then 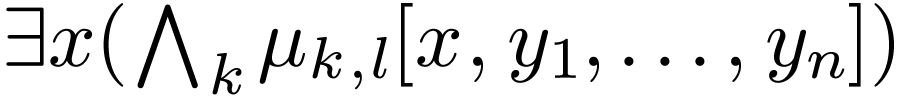 is equivalent to
is equivalent to
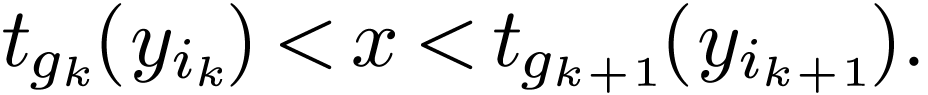
If 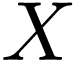 is densely ordered, then this last formula is
always true.
is densely ordered, then this last formula is
always true.
If 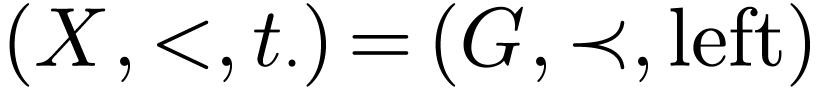 and
and  is not densely
ordered, then consider the least element
is not densely
ordered, then consider the least element  of
of
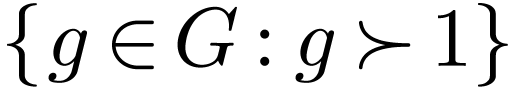 . The formula
. The formula 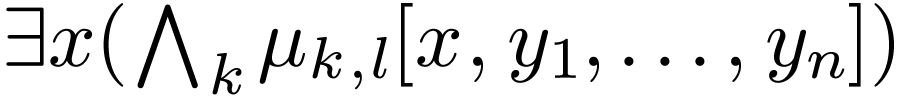 is equivalent to
is equivalent to
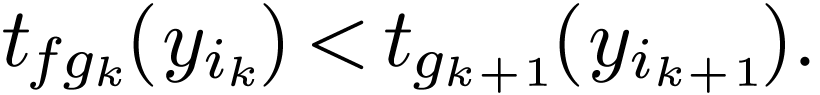
So in any case, the formula 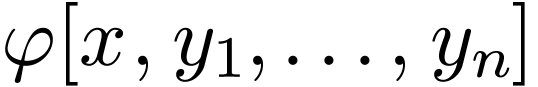 is equivalent to a
quantifier-free formula.
is equivalent to a
quantifier-free formula.
Corollary 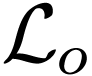 ,
and is thus o-minimal.
,
and is thus o-minimal.
Corollary 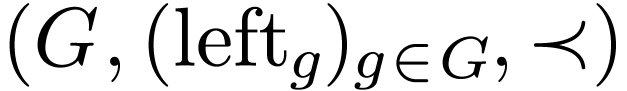 is o-minimal.
is o-minimal.
B. Baizhanov, J. Baldwin, and V. Verbovskiy. Cayley's theorem for ordered groups: o-minimality. Sibirskie Èlektronnye Matematicheskie Izvestiya [electronic only], 4:278–281, 2007.
L. van den Dries. Tame topology and o-minimal structures, volume 248 of London Math. Soc. Lect. Note. Cambridge University Press, 1998.
 holds in
holds in  2
2
atomic formula 1
definable subset 3
first-order language 2
first-order structure 1
 -formula
2
-formula
2
free variable 2
neg-atomic formula 1
o-minimal structure 4
prenex normal form 2
quantifier elimination 3
quantifier-free formula 2
signature 1
term 1
unary representation 5
variable symbol 1