|
|
 .
vincent.bagayoko@lilo.org
.
vincent.bagayoko@lilo.org
Log-atomic numbers are surreal numbers whose iterated logarithms are monomials, i.e. additively irreducible numbers. Presenting surreal numbers as sign sequences, we give the sign sequence formula for log-atomic numbers. In doing so, we relate log-atomic numbers to fixed-points of certain surreal functions.
The class  of surreal numbers
of J. H. Conway [7] is an inductively defined ordered field
with additional structure. Conway uses the abstract notion of Dedekind
inspired cut as a fundamental constructor to define numbers by
well-founded induction.
of surreal numbers
of J. H. Conway [7] is an inductively defined ordered field
with additional structure. Conway uses the abstract notion of Dedekind
inspired cut as a fundamental constructor to define numbers by
well-founded induction.
Indeed, any number  is obtained from sets
is obtained from sets 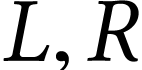 of previously defined numbers, as the
“simplest” number with
of previously defined numbers, as the
“simplest” number with 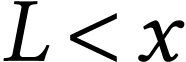 and
and 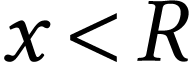 . This relation is denoted
. This relation is denoted 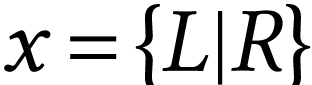 . Conversely, any sets of surreal
numbers
. Conversely, any sets of surreal
numbers 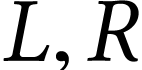 with
with 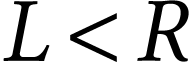 give rise
to a unique simplest number
give rise
to a unique simplest number 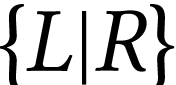 .
Thus the definition of
.
Thus the definition of  comes with several
features: an inductively defined order
comes with several
features: an inductively defined order  ,
an order-saturation property, a corresponding ordinal rank called the
birthday
,
an order-saturation property, a corresponding ordinal rank called the
birthday 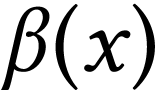 which represents the minimal ordinal
number of inductive steps required to yield
which represents the minimal ordinal
number of inductive steps required to yield 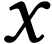 . For instance
. For instance  has birthday
has birthday
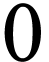 whereas
whereas 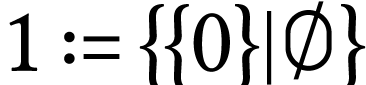 has birthday
has birthday
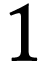 and
and 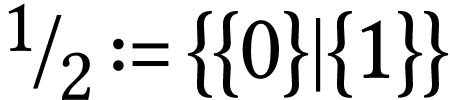 has birthday
has birthday 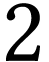 .
.
The versatility of this construction allowed Conway and several authors
after him to define a rich structure on  .
In particular, he defined ring operations that are compatible with the
ordering and turn
.
In particular, he defined ring operations that are compatible with the
ordering and turn 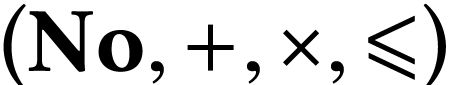 into an ordered field
extension of the reals, as well as an extension of the ordered semi-ring
into an ordered field
extension of the reals, as well as an extension of the ordered semi-ring
 of ordinal numbers under Hessenberg
sum and product.
of ordinal numbers under Hessenberg
sum and product.
Conway also discovered that  enjoys a natural
structure of field of Hahn series as per [10]. Every
surreal number can be expressed as a possibly transfinite sum of
additively irreducible numbers called monomials. Moreover,
monomials can be parametrized by a morphism
enjoys a natural
structure of field of Hahn series as per [10]. Every
surreal number can be expressed as a possibly transfinite sum of
additively irreducible numbers called monomials. Moreover,
monomials can be parametrized by a morphism 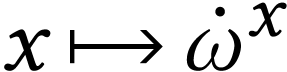 , called the
, called the 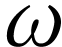 -map,
for which Conway gave a an equation using the cut presentation of
numbers. Whereas the latter presentation is useful to produce inductive
definitions of functions, by induction on the birthday for instance, the
presentation of numbers as Hahn series is useful to compute certain
operations on
-map,
for which Conway gave a an equation using the cut presentation of
numbers. Whereas the latter presentation is useful to produce inductive
definitions of functions, by induction on the birthday for instance, the
presentation of numbers as Hahn series is useful to compute certain
operations on  . In
particular, it can be used to describe H. Gonshor's exponential function
[9], and A. Berarducci and V. Mantova's surreal derivation
[5].
. In
particular, it can be used to describe H. Gonshor's exponential function
[9], and A. Berarducci and V. Mantova's surreal derivation
[5].
The sign sequence presentation of surreal numbers, invented and studied
by H. Gonshor in [9], is a way to give precise description
of surreal numbers. In this picture, numbers are sequences of signs 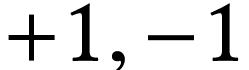 indexed by ordinals, or equivalently, nodes in the
binary tree
indexed by ordinals, or equivalently, nodes in the
binary tree 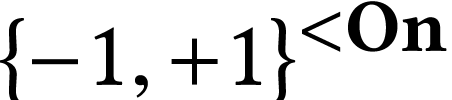 . The birthdate
measure then coincides with the domain, called length, of the
sign sequences. A natural relation of simplicity, which
corresponds to the inclusion of sign sequences in one another and is
denoted
. The birthdate
measure then coincides with the domain, called length, of the
sign sequences. A natural relation of simplicity, which
corresponds to the inclusion of sign sequences in one another and is
denoted 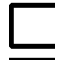 , emerges as a more precise
measure of the complexity of numbers.
, emerges as a more precise
measure of the complexity of numbers.
Sign sequences are by no means an optimal tool to describe surreal
numbers in the context of the ordered field, exponential ordered field,
Hahn series field, or differential field structures. For instance given
numbers 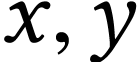 with known sign sequences, computing the
sign sequence of
with known sign sequences, computing the
sign sequence of  , or even
formulating the properties of that of
, or even
formulating the properties of that of 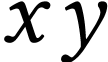 in general
are open problems. However, sign sequences behave relatively well with
respect to operations that preserve simplicity under certain conditions.
This includes the
in general
are open problems. However, sign sequences behave relatively well with
respect to operations that preserve simplicity under certain conditions.
This includes the 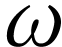 -map, the
transfinite summation which identifies numbers with Hahn series, and the
exponentiation of monomials. In this context, sign sequences can be
useful tools to understand the behavior of length under the operations,
as well as deriving general properties of certain classes of numbers
with respect to the relations
-map, the
transfinite summation which identifies numbers with Hahn series, and the
exponentiation of monomials. In this context, sign sequences can be
useful tools to understand the behavior of length under the operations,
as well as deriving general properties of certain classes of numbers
with respect to the relations 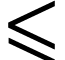 and
and 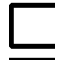 .
.
Describing the sign sequences of elements in a class  often requires a reference with respect to which they can be given. One
way to give such a reference is to find a parametrization of
often requires a reference with respect to which they can be given. One
way to give such a reference is to find a parametrization of  , i.e. a bijection
, i.e. a bijection 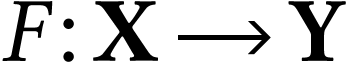 for a certain subclass
for a certain subclass 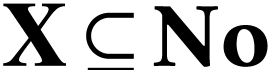 , and
then describe the sign sequence of
, and
then describe the sign sequence of 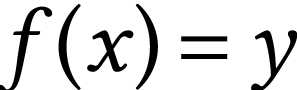 in terms of
that of
in terms of
that of 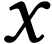 for each
for each 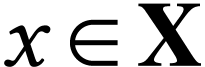 .
This presumes that the behavior of function
.
This presumes that the behavior of function 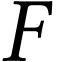 on
sign sequences may be understood, suggesting that
on
sign sequences may be understood, suggesting that 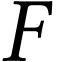 should be compatible in a sense with the relations
should be compatible in a sense with the relations 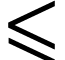 and
and 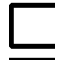 . There enters the notion
of surreal substructure of [3]. Surreal substructures are
subclasses
. There enters the notion
of surreal substructure of [3]. Surreal substructures are
subclasses 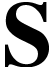 of
of  that are
isomorphic to
that are
isomorphic to 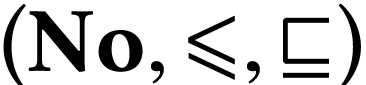 under the restrictions of
under the restrictions of 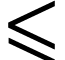 and
and  to
to  . The isomorphism
. The isomorphism 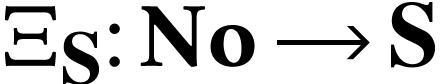 then being
unique, one may rely on it to relate the sign sequence of
then being
unique, one may rely on it to relate the sign sequence of 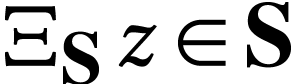 with that of
with that of 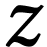 .
.
Surreal substructures naturally appear when defining certain operations
on  , see for instance [3, Sections 6 and 7]. The study of surreal substructure yields
tools to express and compute sign sequences. In particular, expressing a
structure
, see for instance [3, Sections 6 and 7]. The study of surreal substructure yields
tools to express and compute sign sequences. In particular, expressing a
structure 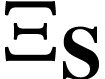 using classes of fixed points for
given parametrizations yields a method to compute the sign sequence
formula of
using classes of fixed points for
given parametrizations yields a method to compute the sign sequence
formula of 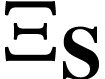 . Relying
extensively on [3], we will develop the relevant notions in
Sections 1 and 2.
. Relying
extensively on [3], we will develop the relevant notions in
Sections 1 and 2.
A surreal substructure of particular interest is the class  of log-atomic numbers. Those are numbers
of log-atomic numbers. Those are numbers 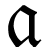 such that the
such that the 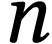 -fold
iteration of
-fold
iteration of 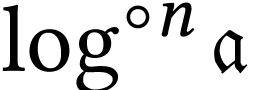 of the logarithm at
of the logarithm at 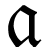 yields a monomial for each
yields a monomial for each 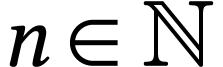 .
This structure plays a crucial role in the definition of derivations on
.
This structure plays a crucial role in the definition of derivations on
 that are compatible with the exponential and the
structure of field of series of
that are compatible with the exponential and the
structure of field of series of  .
It is also used in the investigation of the properties of expansions of
numbers as transseries. This class was characterized by Berarducci and
Mantova [5, Section 5] who defined such a derivation and
proved a fundamental structure property for
.
It is also used in the investigation of the properties of expansions of
numbers as transseries. This class was characterized by Berarducci and
Mantova [5, Section 5] who defined such a derivation and
proved a fundamental structure property for  . Finally
. Finally  plays a role in
the definition of the first surreal hyperexponential function
plays a role in
the definition of the first surreal hyperexponential function 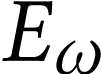 [4]. Our our goal in this article is to
compute the sign sequence formula for
[4]. Our our goal in this article is to
compute the sign sequence formula for  .
This will in particular give the sign sequence for
.
This will in particular give the sign sequence for 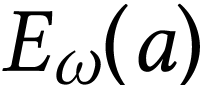 for each surreal number
for each surreal number 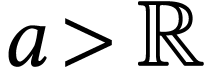 whose length is strictly
below the first
whose length is strictly
below the first 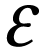 -number
-number 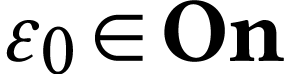 .
.
In this task, we are continuing work of S. Kuhlmann and M. Matusinski in
[13]. Indeed, they considered a surreal substructure 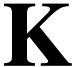 properly contained in
properly contained in 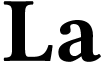 and
determined its sign sequence formula. The relation between
and
determined its sign sequence formula. The relation between 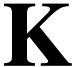 and
and 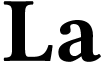 was subject to the conjecture
was subject to the conjecture
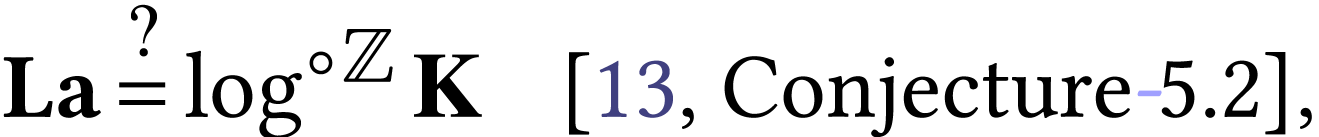
which turned out to be false [5, Proposition 5.24]. The
correct relation between 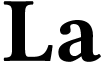 and
and 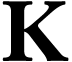 was later found by Mantova and Matusinski [14]. We will
rely on their sign sequence formula and a presentation of
was later found by Mantova and Matusinski [14]. We will
rely on their sign sequence formula and a presentation of  using classes of fixed points to derive our formula.
using classes of fixed points to derive our formula.
As Gonshor, we define numbers as sign sequences.
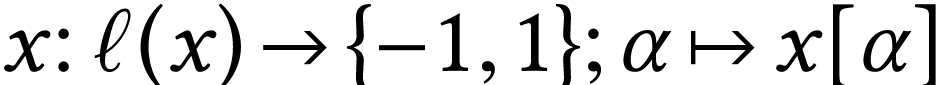 , where
, where 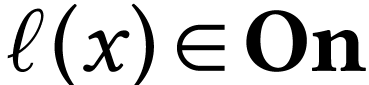 is an ordinal number. We call
is an ordinal number. We call 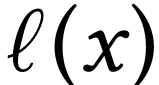 the
the 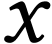 and the map
and the map 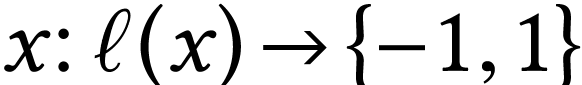 the
the 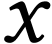 .
We write
.
We write  for the class of surreal numbers.
for the class of surreal numbers.
Given a surreal number  , we
extend its sign sequence with
, we
extend its sign sequence with 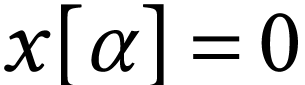 for all
for all 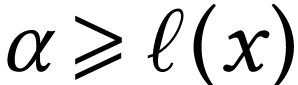 . Given
. Given  and
and
 , we also introduce the
restriction
, we also introduce the
restriction 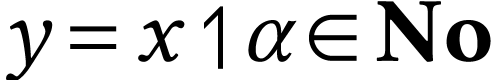 to
to 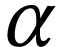 as being the initial segment of
as being the initial segment of 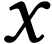 of length
of length 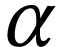 , i.e.
, i.e. 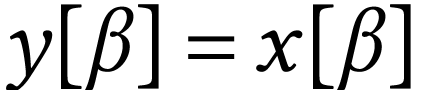 for
for
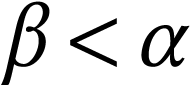 and
and 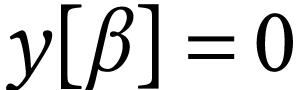 for
for 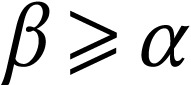 .
.
The ordering 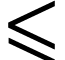 on
on  is
lexicographical: given distinct elements
is
lexicographical: given distinct elements 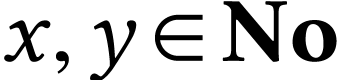 ,
there exists a smallest ordinal
,
there exists a smallest ordinal 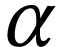 with
with 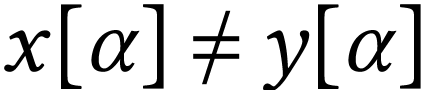 and we set
and we set 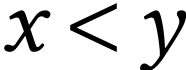 if and only if
if and only if  .
.
For 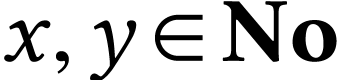 , we say that
, we say that 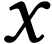 is simpler than
is simpler than 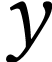 , and write
, and write  , if
, if
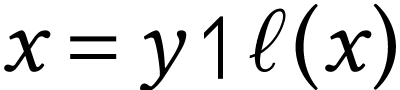 . The partially ordered class
. The partially ordered class
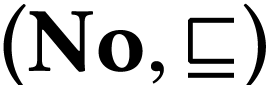 is well-founded. We write
is well-founded. We write  if
if  and
and 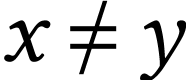 .
For
.
For  , we write
, we write

for the set of numbers that are strictly simpler than 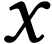 . The set
. The set 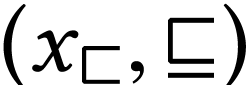 is
well-ordered with order type
is
well-ordered with order type 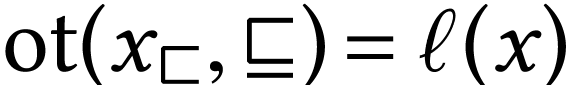 .
Moreover,
.
Moreover, 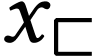 is the union of the sets
is the union of the sets
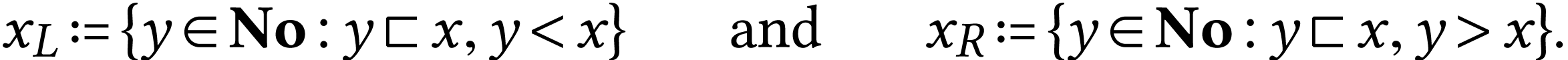
Every linearly ordered subset 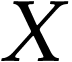 of
of 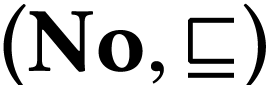 has a supremum
has a supremum 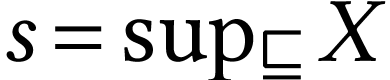 in
in  . Indeed, we have
. Indeed, we have 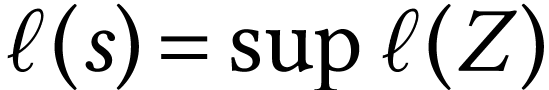 , and
, and 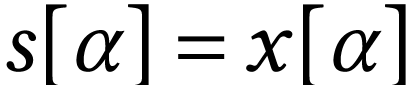 for
all
for
all 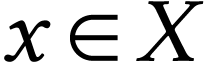 with
with 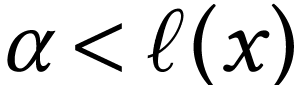 .
Numbers
.
Numbers 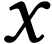 that are equal to
that are equal to 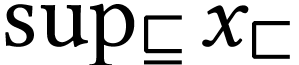 are called limit numbers; other numbers are called
successor numbers. Limit numbers are exactly the
numbers whose length is a limit ordinal.
are called limit numbers; other numbers are called
successor numbers. Limit numbers are exactly the
numbers whose length is a limit ordinal.
Notice that  is a proper class. For instance, the
linearly ordered class
is a proper class. For instance, the
linearly ordered class 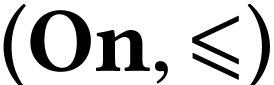 is embedded into the
partial order
is embedded into the
partial order 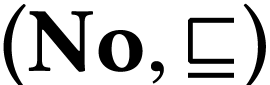 through the map
through the map 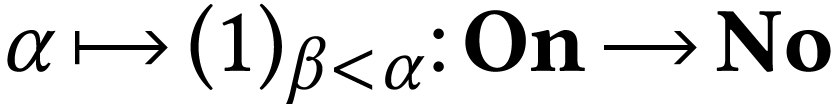 . We will thus identify ordinals numbers as
surreal numbers.
. We will thus identify ordinals numbers as
surreal numbers.
Any non-archimedean ordered field 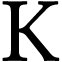 admits a
non-trivial valuation called the natural valuation [1,
Section 3.5]. The natural valuation of
admits a
non-trivial valuation called the natural valuation [1,
Section 3.5]. The natural valuation of 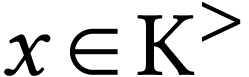 is
related to its archimedean class, i.e. the class
is
related to its archimedean class, i.e. the class
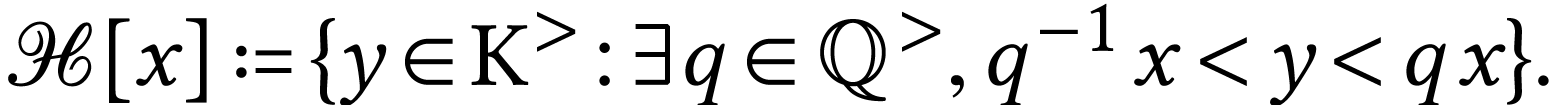
In NBG, the corresponding valued ordered field can be embedded [11] into a field of generalized Hahn series, as defined by Hahn [10]. The existence of such embeddings, called Kaplansky embeddings, usually requires the axiom of choice.
Having defined the structure of ordered field, Conway noticed that for
 , the instances where choice
is required could be circumvented by the use of the inductive nature of
, the instances where choice
is required could be circumvented by the use of the inductive nature of
 . Indeed, in
. Indeed, in  , each archimedean class
, each archimedean class 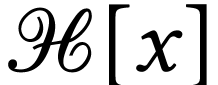 has a unique
has a unique 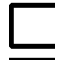 -minimal element
denoted
-minimal element
denoted 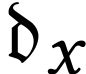 , and the class
, and the class 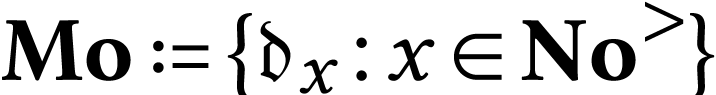 is a subgroup of
is a subgroup of 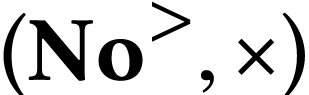 which
can be used to carry the definition of the Kaplansky embedding.
which
can be used to carry the definition of the Kaplansky embedding.
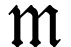 which is simplest in the class
which is simplest in the class 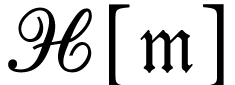 ,
i.e. a number of the form
,
i.e. a number of the form 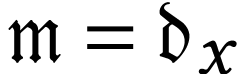 for a certain
for a certain  .
.
Moreover, Conway defined a parametrization 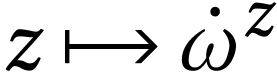 of
of  . This is a strictly
increasing morphism
. This is a strictly
increasing morphism 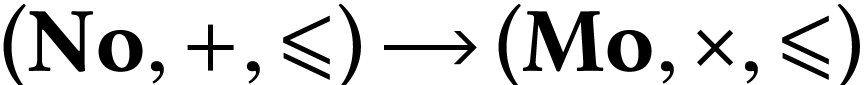 which also preserves
simplicity:
which also preserves
simplicity:
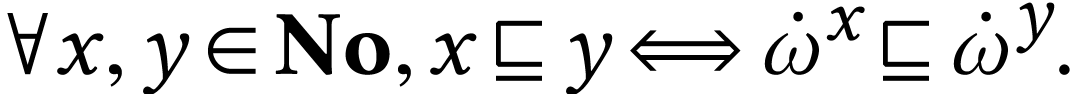
The operation  coincides with the ordinal
exponentiation with basis
coincides with the ordinal
exponentiation with basis 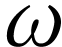 .
.
For ordinals 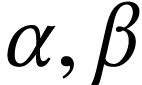 , we will denote
their ordinal sum, product, and exponentiation by
, we will denote
their ordinal sum, product, and exponentiation by 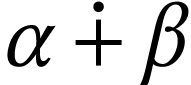 ,
, 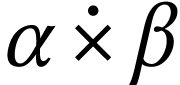 and
and 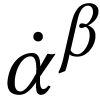 . Here, we introduce the operations
. Here, we introduce the operations  and
and
 of [3, Section 3.2] on
of [3, Section 3.2] on  . Those are natural extensions of ordinal
arithmetic to
. Those are natural extensions of ordinal
arithmetic to  , which we will
use in order to describe sign sequences.
, which we will
use in order to describe sign sequences.
For numbers 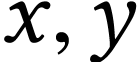 , we write
, we write 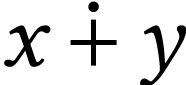 for the number whose sign sequence is the
concatenation of that of
for the number whose sign sequence is the
concatenation of that of 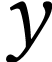 at the end of that of
at the end of that of
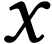 . So
. So  is the number of length
is the number of length 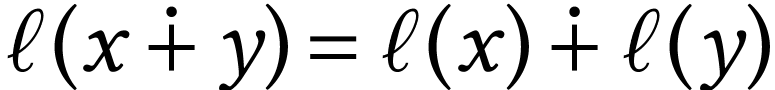 ,
which satisfies
,
which satisfies
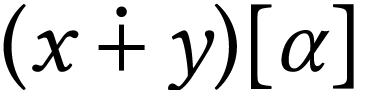 |
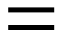 |
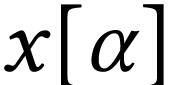 |
(α<ℓ(x)) |
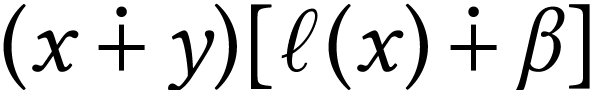 |
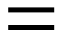 |
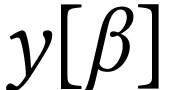 |
(β<ℓ(y)) |
The operation  clearly extends ordinal sum. We
have
clearly extends ordinal sum. We
have 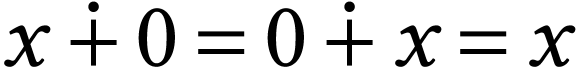 for all
for all  .
.
We write 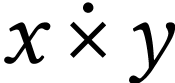 for the number of length
for the number of length
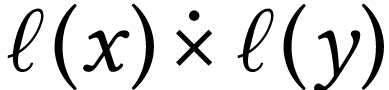 whose sign sequence is defined by
whose sign sequence is defined by
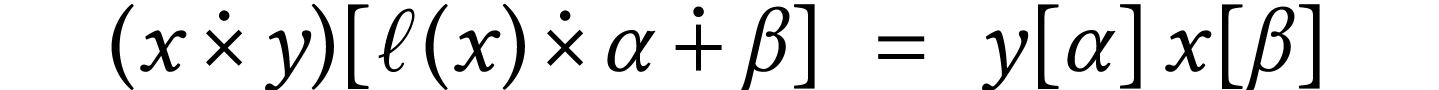 |
(α<ℓ(y),β<ℓ(x)) |
The operation  extends ordinal product. Special
cases can be described informally: given
extends ordinal product. Special
cases can be described informally: given  and
and
 , the number
, the number  is the concatenation of
is the concatenation of 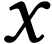 with itself to the right
“
with itself to the right
“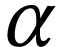 -many times”,
whereas
-many times”,
whereas  is the number obtained from
is the number obtained from 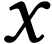 by replacing each sign by itself
by replacing each sign by itself 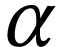 -many times. We have
-many times. We have 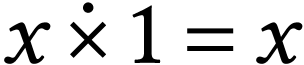 and
and
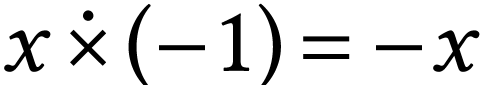 for all
for all  .
.
The operations also enjoy the properties which extend that of their ordinal counterparts as is illustrated hereafter. We refer to [3, Section 3.2] for more details.
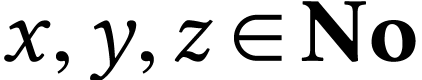 ,
we have
,
we have
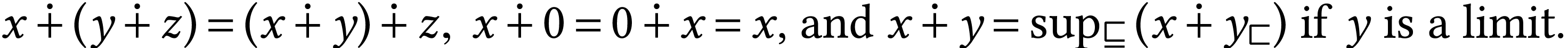
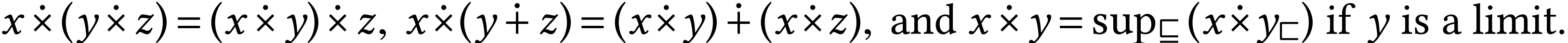
If 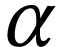 is an ordinal and
is an ordinal and 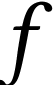 is
a function
is
a function 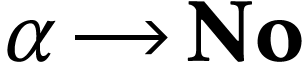 , then
, then 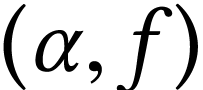 uniquely determines a surreal number
uniquely determines a surreal number 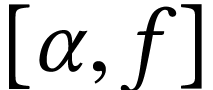 defined inductively by the rules
defined inductively by the rules
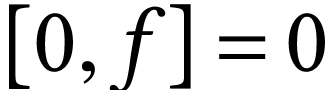 ,
,
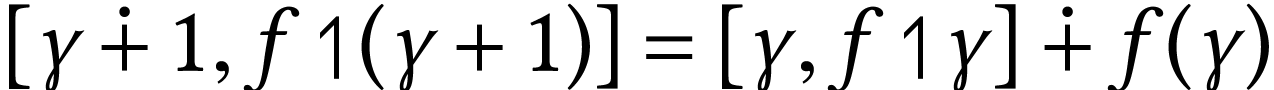 for
for 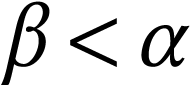 ,
,
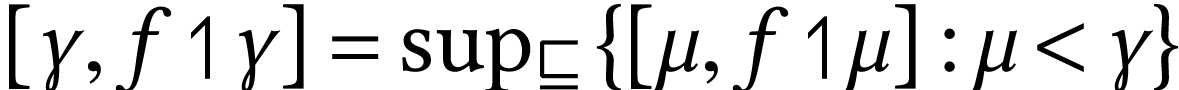 for limit ordinals
for limit ordinals 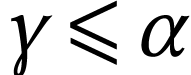 .
.
We say that 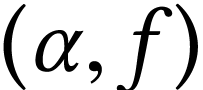 is a sign sequence
formula for
is a sign sequence
formula for 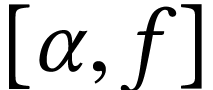 ,
which we identify with the informal expression
,
which we identify with the informal expression
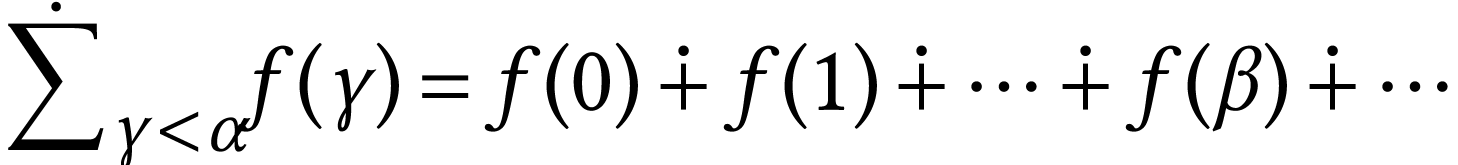
where  ranges in
ranges in  .
For instance, the ordered pair
.
For instance, the ordered pair 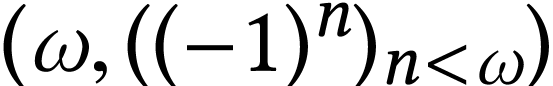 is a sign
sequence formula of
is a sign
sequence formula of 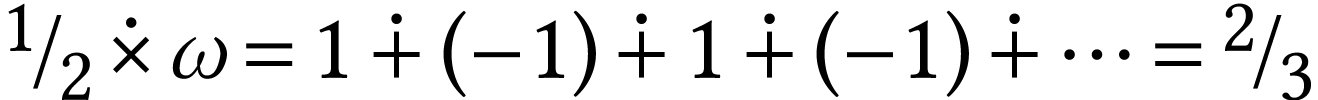 . In
general, we look for such formulas where
. In
general, we look for such formulas where 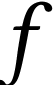 alternates between
alternates between  and
and  , that is, where
, that is, where 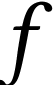 ranges in
ranges in
 and where, for each ordinal
and where, for each ordinal 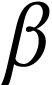 with
with 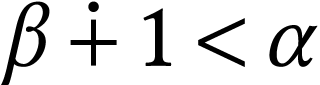 , we have
, we have 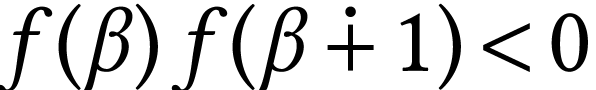 . It is easy to see that every surreal number
admits a unique such alternating sign sequence formula. We refer to this
formula as the sign sequence formula of said number.
. It is easy to see that every surreal number
admits a unique such alternating sign sequence formula. We refer to this
formula as the sign sequence formula of said number.
If 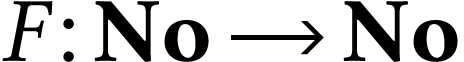 is a function, we may look for a function
is a function, we may look for a function
 whose value at each number
whose value at each number 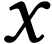 is a sign sequence formula of
is a sign sequence formula of 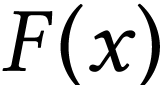 .
We then consider
.
We then consider  as a sign sequence
formula for
as a sign sequence
formula for 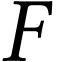 .
.
As an example, we now state Gonshor's results regarding the sign
sequences of monomials. For  ,
we write
,
we write 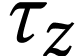 for the order type of
for the order type of 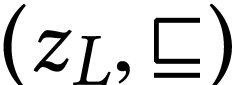 , that is the order type
, that is the order type 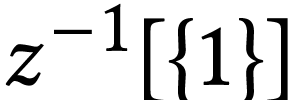 when
when 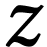 is seen as a sign sequence, or equivalently
the ordinal number of signs
is seen as a sign sequence, or equivalently
the ordinal number of signs 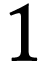 in the sign sequence
of
in the sign sequence
of 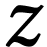 . We have
. We have 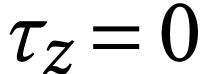 if and only if
if and only if 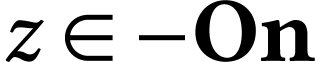 . Gonshor
found the following sign sequence formula for monomials:
. Gonshor
found the following sign sequence formula for monomials:
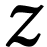 be a number.
The sign sequence formula for
be a number.
The sign sequence formula for 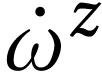 is
is
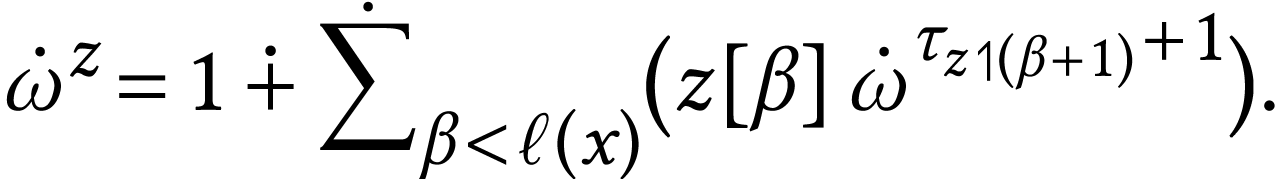
For instance, we have
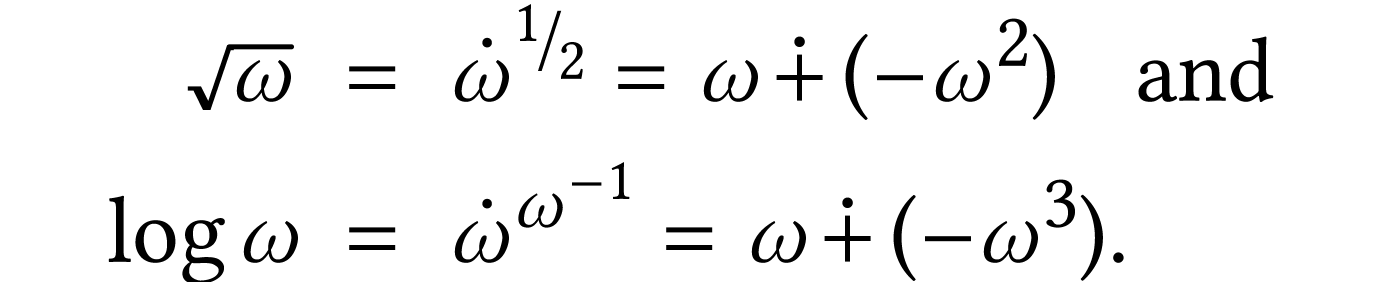
Let us also specify a consequence that we will use often in what follows.
 be such that the maximal ordinal
be such that the maximal ordinal 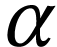 with
with  is a limit. We have
is a limit. We have 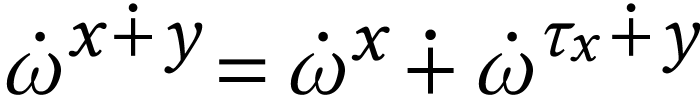 .
.
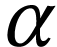 be maximal with
be maximal with
 and write
and write 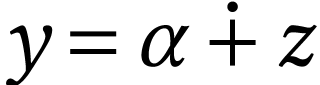 .
Since
.
Since 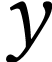 is strictly positive, we have
is strictly positive, we have 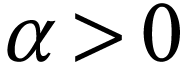 , whence
, whence 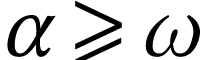 .
Let
.
Let
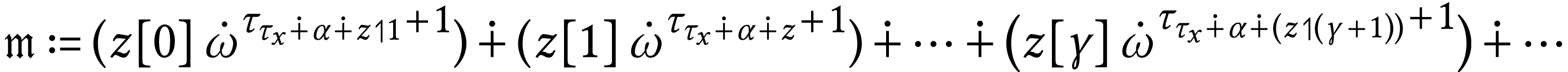
where 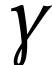 ranges in
ranges in 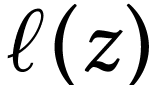 .
Proposition 4 yields
.
Proposition 4 yields 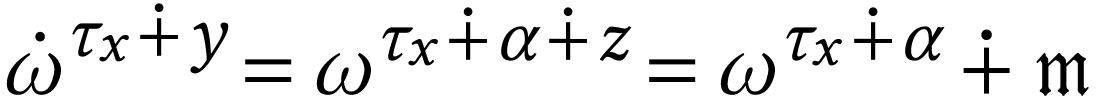 .
On the other hand, we have
.
On the other hand, we have 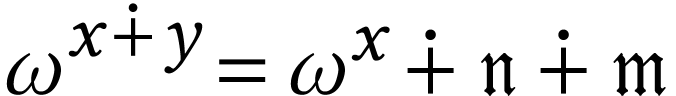 where
where 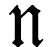 is defined as the transfinite concatenation
is defined as the transfinite concatenation

where 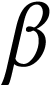 ranges in
ranges in 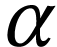 .
For
.
For 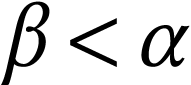 , we have
, we have 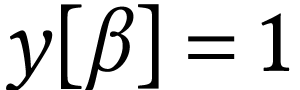 and
and 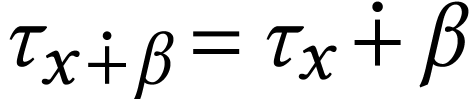 , so
, so
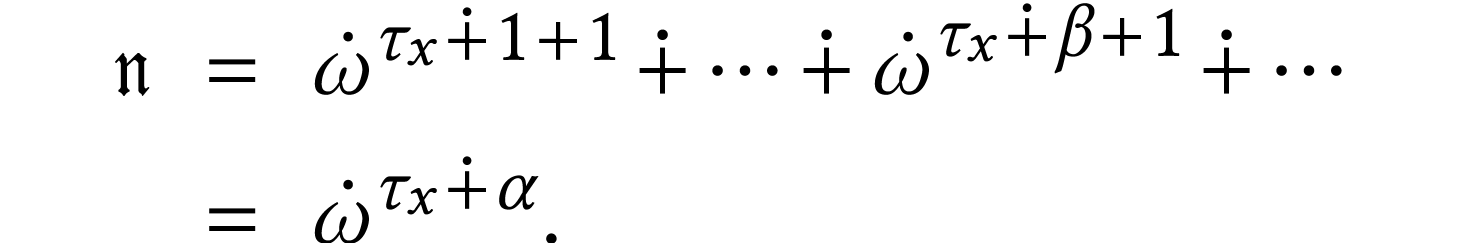
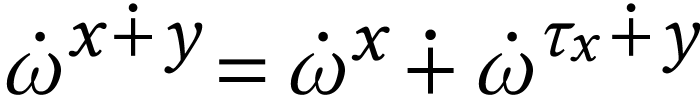 .
.

 of
of  such that
such that 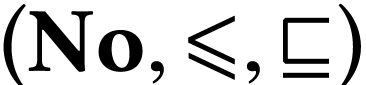 and
and 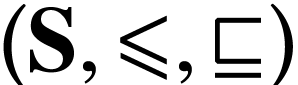 are isomorphic. The isomorphism
are isomorphic. The isomorphism 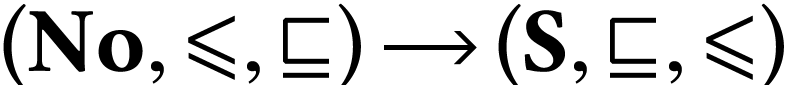 is unique, denoted
is unique, denoted 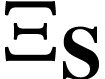 and called the
parametrization of
and called the
parametrization of 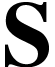 .
.
Example
For  , the class
, the class 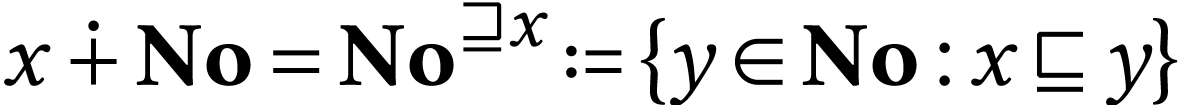 has parametrization
has parametrization 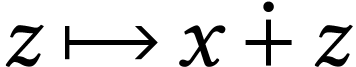 .
We have
.
We have
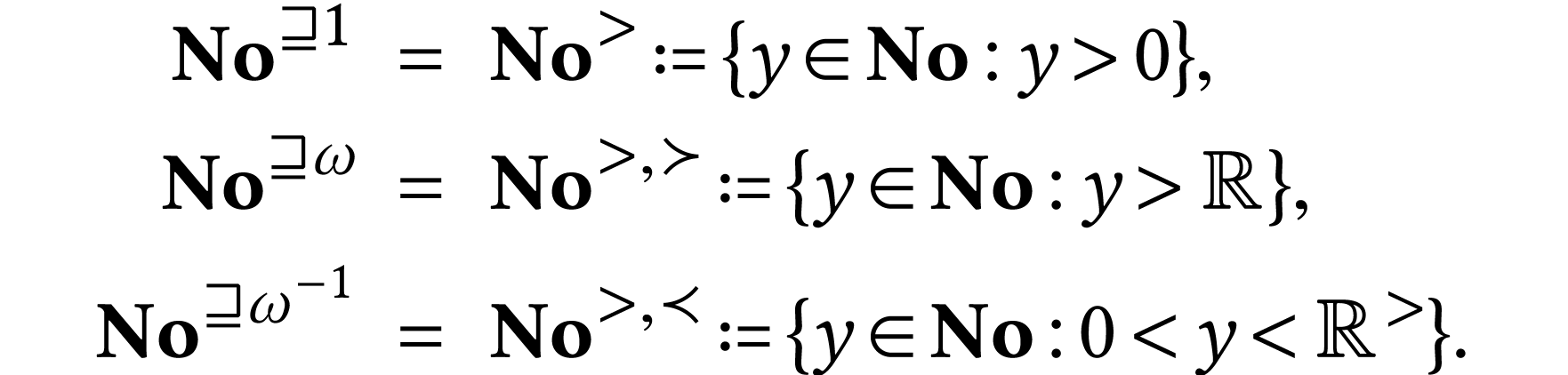
For  , the class
, the class 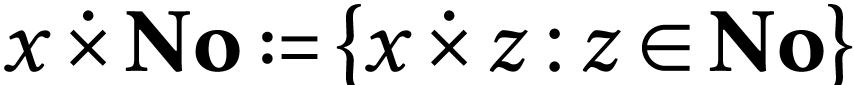 has parametrization
has parametrization 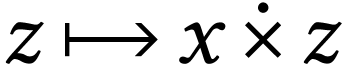 .
We have
.
We have
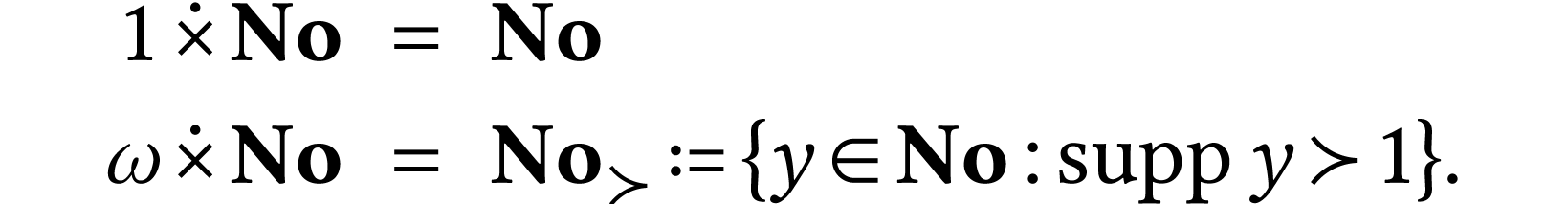
The class  of monomials has parametrization
of monomials has parametrization
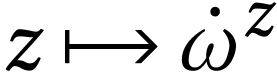 .
.
Let 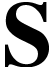 be a surreal substructure and let
be a surreal substructure and let  be a convex subclass of
be a convex subclass of 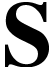 . This means that for
. This means that for 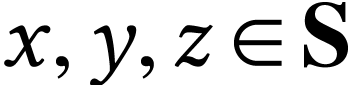 with
with
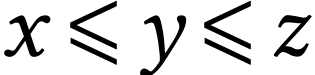 , we have
, we have 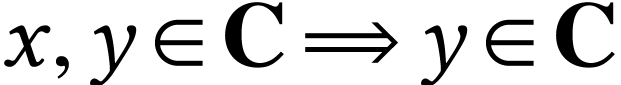 . Then we have a simple criterion to decide
whether
. Then we have a simple criterion to decide
whether  is a surreal substructure:
is a surreal substructure:
 of
of 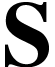 is a surreal substructure if and only if
every subset of
is a surreal substructure if and only if
every subset of  has strict upper and lower
bounds in
has strict upper and lower
bounds in  .
.
In particular, non-empty open intervals 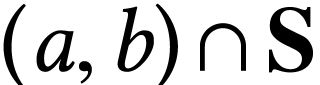 ,
where
,
where 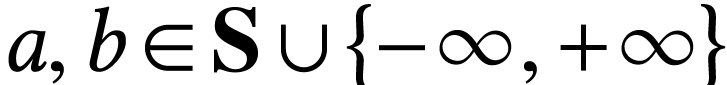 , are surreal
substructures. The following proposition gives a sign sequence formula
for
, are surreal
substructures. The following proposition gives a sign sequence formula
for 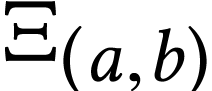 in certain particular cases.
in certain particular cases.
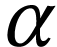 be a non-zero ordinal. Let
be a non-zero ordinal. Let 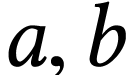 and
and 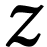 be numbers.
be numbers.
 if and only if
if and only if 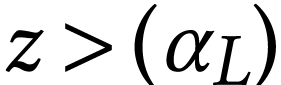 and
and 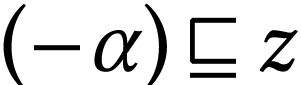 if
and only if
if
and only if 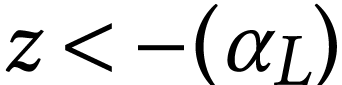 so the given descriptions cover all
cases. We will only derive the formulas for the interval
so the given descriptions cover all
cases. We will only derive the formulas for the interval 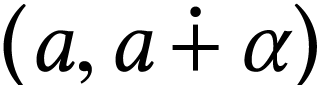 , the other ones being symmetric. The number
, the other ones being symmetric. The number
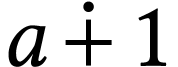 is the root of
is the root of 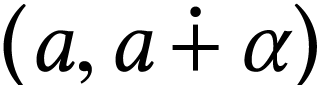 so for
so for
 , we have
, we have 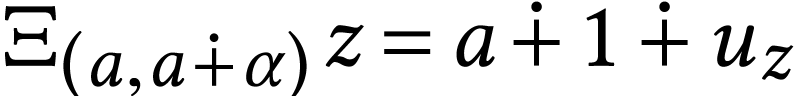 for a certain number
for a certain number 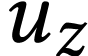 . The
class
. The
class 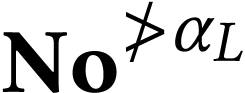 is convex in
is convex in  and
for
and
for  , we have
, we have 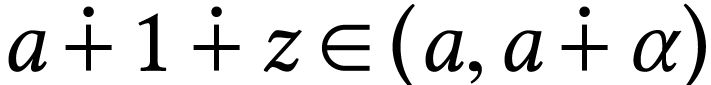 . The function
. The function 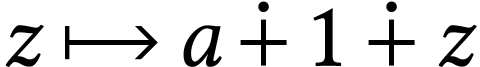 defined
on
defined
on  defines a surreal isomorphism, so we have
defines a surreal isomorphism, so we have
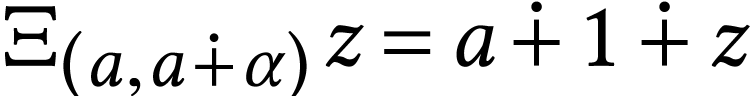 if
if  .
On the other hand, we have
.
On the other hand, we have
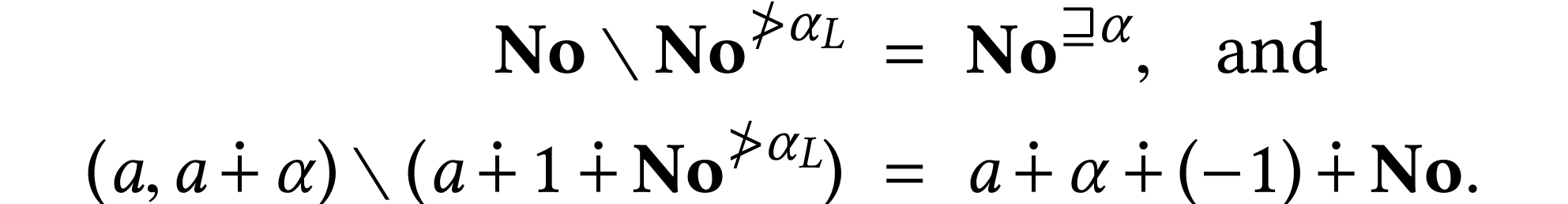
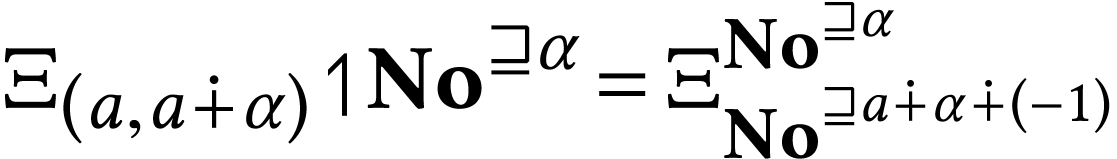 , which
yields the other part of the description.
, which
yields the other part of the description.

Let 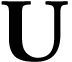 ,
,  be two surreal substructures. Then there is a unique
be two surreal substructures. Then there is a unique 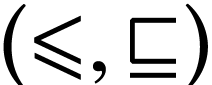 -isomorphism
-isomorphism

that we call the surreal isomorphism
between 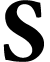 and
and  .
The composition
.
The composition  is also an embedding, so its
image
is also an embedding, so its
image  is again a surreal substructure
that we call the imbrication of
is again a surreal substructure
that we call the imbrication of  into
into 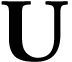 . Given
. Given 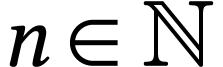 , we write
, we write 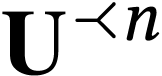 for the
for the
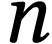 -fold imbrication of
-fold imbrication of  into itself. We have
into itself. We have 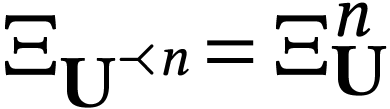 .
.
Example 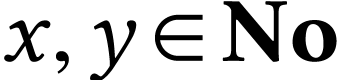 , it follows from Lemma 3 that we have
, it follows from Lemma 3 that we have
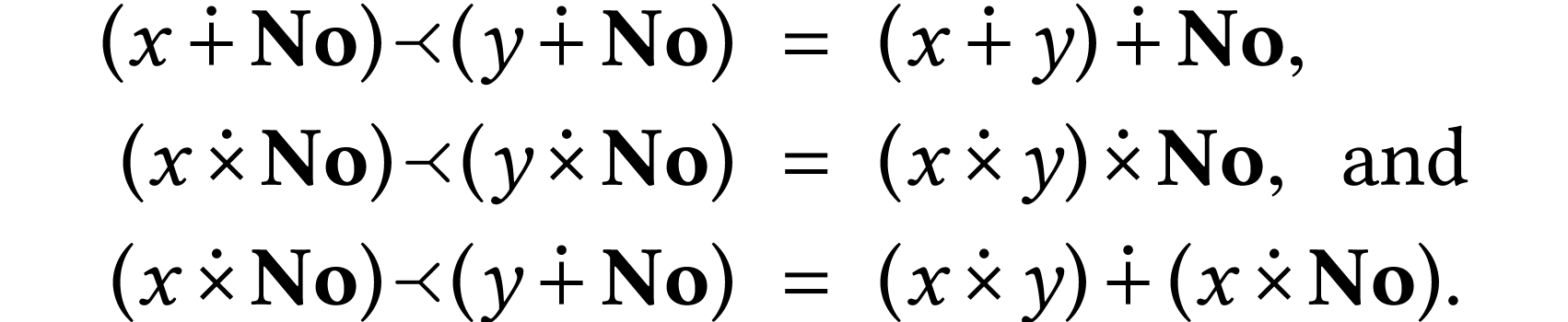
Less elementary results include the relation 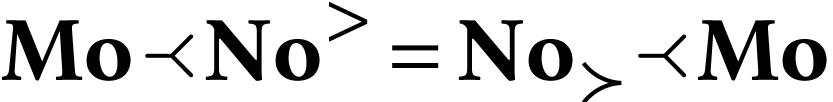 of
[3, Proposition 7.3].
of
[3, Proposition 7.3].
The relation of imbrication is related to the inclusion of surreal substructures in the following way:
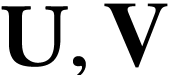 , we have
, we have 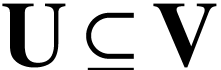 if and only if there is a surreal substructure
if and only if there is a surreal substructure 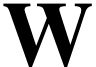 with
with 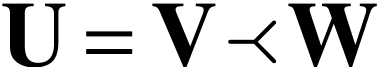 .
.
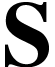 be a surreal substructure. We say that a number
be a surreal substructure. We say that a number 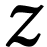 is
is 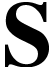 -fixed if
-fixed if 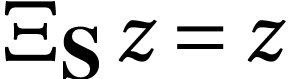 . We write
. We write 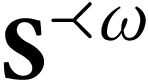 for the class of
for the class of 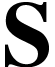 -fixed numbers.
-fixed numbers.
If 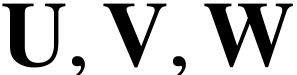 are surreal substructures with
are surreal substructures with 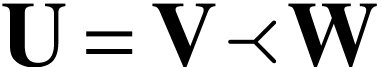 , then the class
, then the class 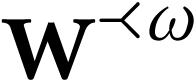 is
that of numbers
is
that of numbers 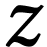 with
with 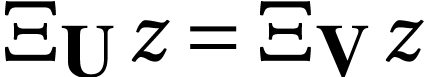 .
.
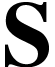 is a
surreal substructure, then
is a
surreal substructure, then 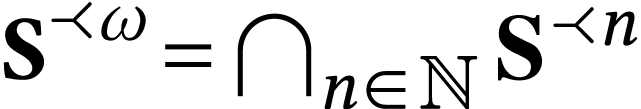 .
.
Notice that 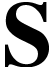 may not itself be a surreal
substructure in general. We thus consider the following notion of
closure:
may not itself be a surreal
substructure in general. We thus consider the following notion of
closure:
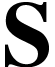 is closed if we
have
is closed if we
have 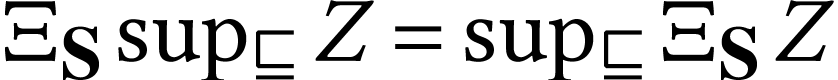 for all non-empty set
for all non-empty set 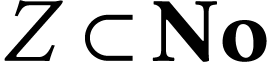 such that
such that 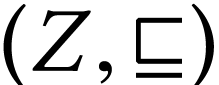 is linearly ordered.
is linearly ordered.
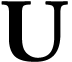 and
and 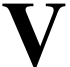 are closed surreal substructures, then so is
are closed surreal substructures, then so is 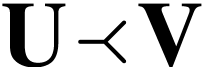 .
.
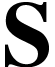 is closed,
then
is closed,
then 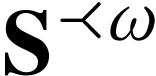 is a closed surreal substructure.
is a closed surreal substructure.
In general, when 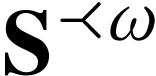 is a surreal substructure, we
write
is a surreal substructure, we
write 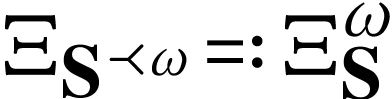 .
.
Example
For  , the structure
, the structure 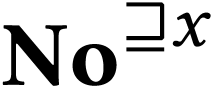 is closed, with
is closed, with 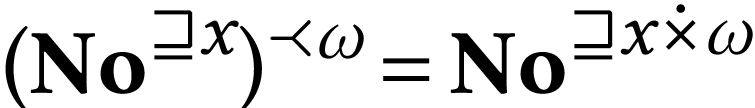 .
.
For  , the structure
, the structure 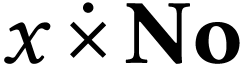 is closed, with
is closed, with 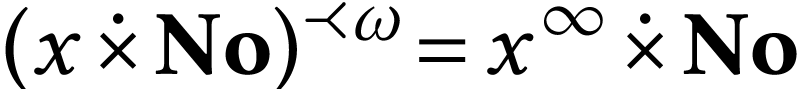 where
where
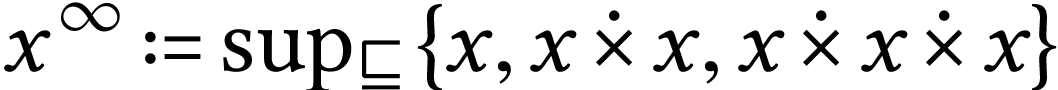 .
.
The structure 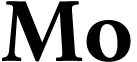 is closed, and the
parametrization
is closed, and the
parametrization 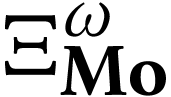 of
of 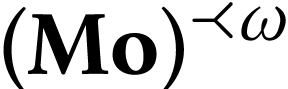 is usually denoted
is usually denoted 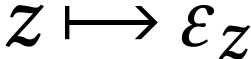 , since it
extends the ordinal function
, since it
extends the ordinal function 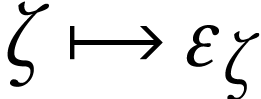 which
parametrizes the fixed points of
which
parametrizes the fixed points of 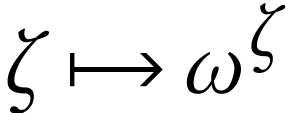 .
.
The structure 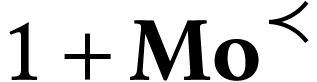 (where
(where 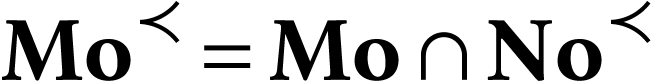 ) is closed. Moreover, its structure of fixed
points
) is closed. Moreover, its structure of fixed
points  coincides with the class of fixed
points of the function
coincides with the class of fixed
points of the function 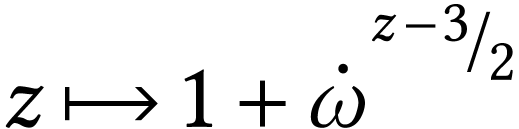 ,
although this last one is not a surreal isomorphism. Informal
expansions
,
although this last one is not a surreal isomorphism. Informal
expansions
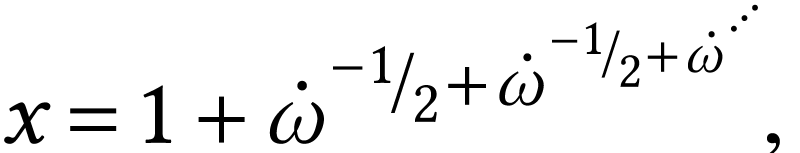
of numbers in this class can be replaced by the formulation 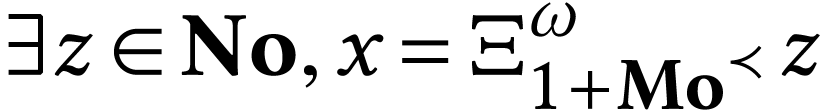 . The sign sequence of
. The sign sequence of 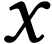 can be computed in terms of that of
can be computed in terms of that of 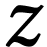 using Proposition 19 below.
using Proposition 19 below.
Let 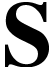 be a closed surreal substructure and let
be a closed surreal substructure and let
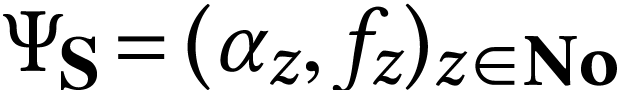 denote its alternating sign sequence formula.
This formula is “continuous” or “closed” in the
sense that for any limit number
denote its alternating sign sequence formula.
This formula is “continuous” or “closed” in the
sense that for any limit number 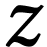 ,
we have
,
we have 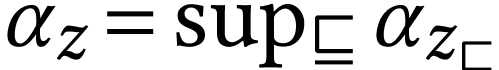 and
and  .
If for each surreal number
.
If for each surreal number  and for
and for 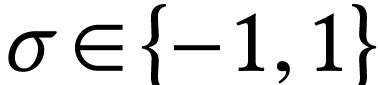 we write
we write 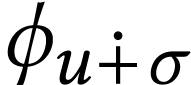 for the non-zero surreal
number defined by
for the non-zero surreal
number defined by 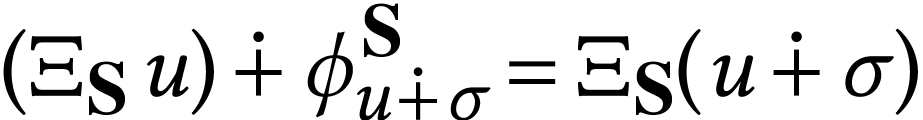 , we then
have
, we then
have
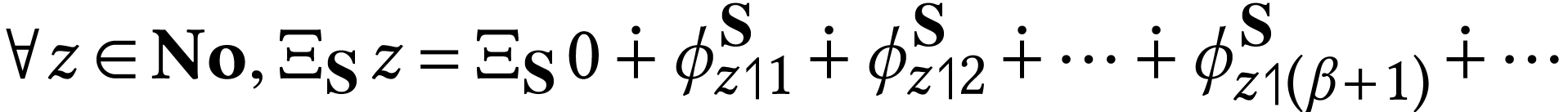
where  ranges in
ranges in  .
Thus it is enough to compute the numbers
.
Thus it is enough to compute the numbers 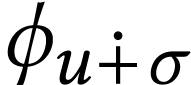 to
determine sign sequences of element of
to
determine sign sequences of element of  .
In the case in Gonshor's formulas for the
.
In the case in Gonshor's formulas for the 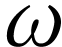 -map
and the
-map
and the 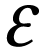 -map and
Kuhlmann-Matusinski's formula for the
-map and
Kuhlmann-Matusinski's formula for the  -map,
those numbers are ordinals or opposites of ordinals. If
-map,
those numbers are ordinals or opposites of ordinals. If 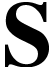 is not closed, then for every limit number
is not closed, then for every limit number  for
which there will be an additional term
for
which there will be an additional term 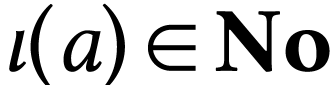 such that
such that
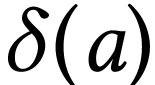 is not always zero, and that we have, for all
is not always zero, and that we have, for all
 ,
,
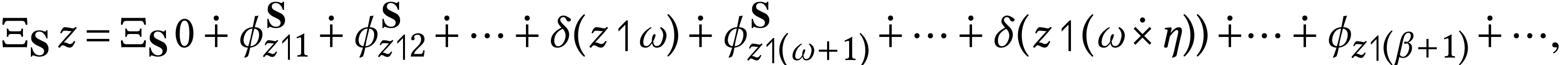
where 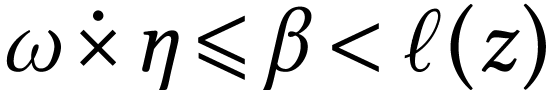 . Such terms
. Such terms 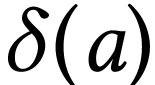 must then be computed independently. Thus it may be a good
first step towards computing a sign sequence formula for
must then be computed independently. Thus it may be a good
first step towards computing a sign sequence formula for 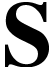 to check whether it is closed or not, and where closure
defects occur.
to check whether it is closed or not, and where closure
defects occur.
Example 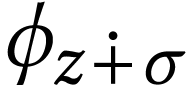 for the
for the 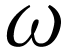 -map are
-map are
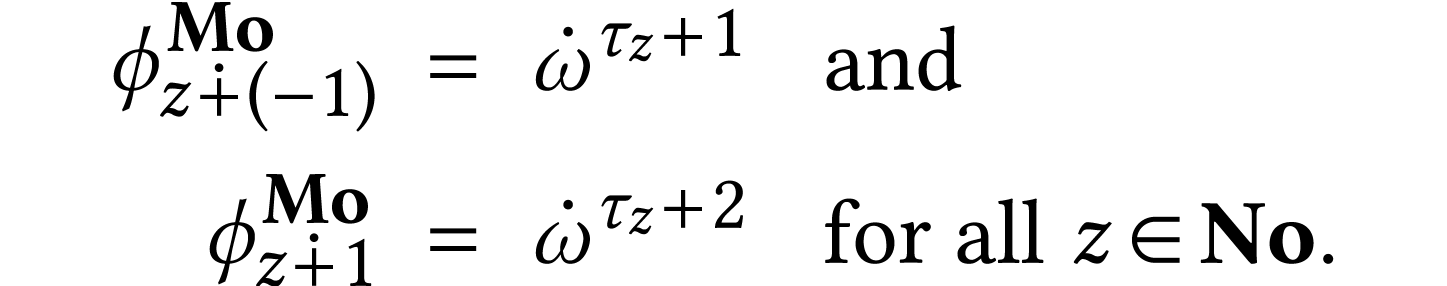
By [9, Chapter 9], the sign sequence formula for 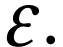 is given by the parameters:
is given by the parameters:
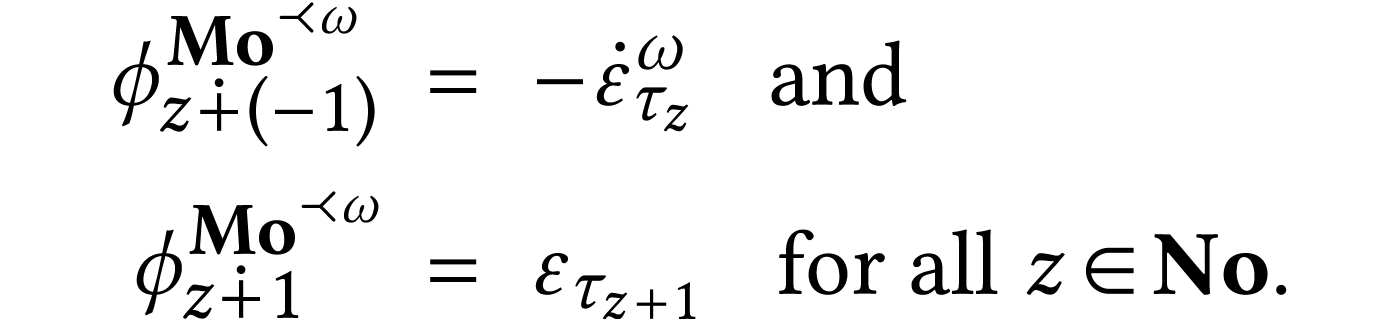
Assume again that 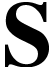 is a closed surreal
substructure and let
is a closed surreal
substructure and let  . Our
goal in this paragraph is to compute
. Our
goal in this paragraph is to compute 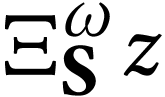 provided we
know
provided we
know 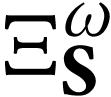 on
on  .
The identity
.
The identity 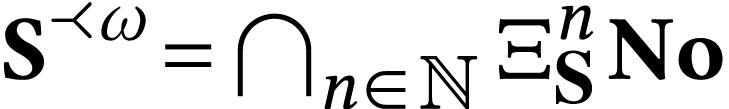 suggests that
suggests that 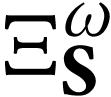 may be a form of limit of
may be a form of limit of  as
as 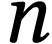 tends to infinity. Indeed, we claim that one can always find
tends to infinity. Indeed, we claim that one can always find  such that
such that 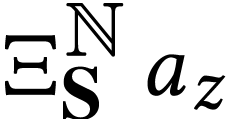 is a
is a  -chain with supremum
-chain with supremum 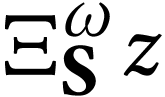 . More precisely, we have:
. More precisely, we have:
 is a closed surreal substructure and let
is a closed surreal substructure and let  . We have
. We have
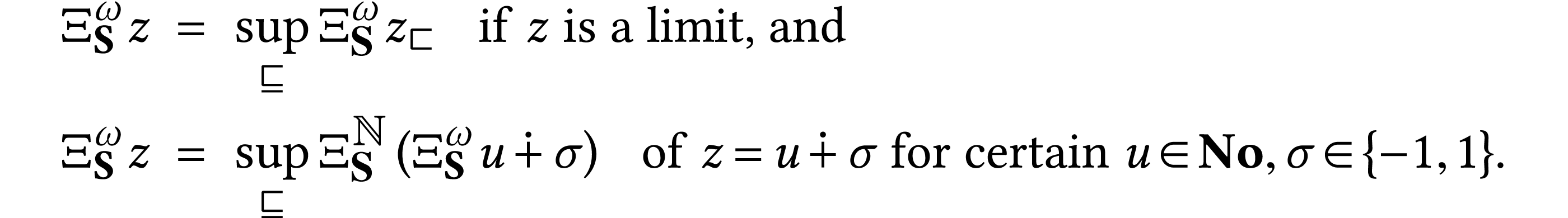
 ,
and set
,
and set  . Since
. Since  is closed, so is
is closed, so is 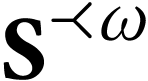 ,
which implies that
,
which implies that 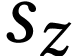 is
is 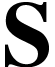 -fixed.
-fixed.
Assume that 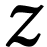 is a limit number. Notice that
is a limit number. Notice that 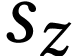 is the simplest element of
is the simplest element of 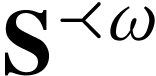 with
with 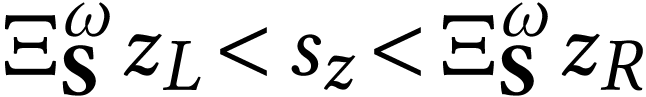 , whereas
, whereas 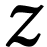 is the simplest number with
is the simplest number with 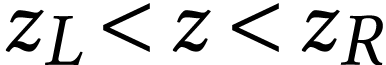 .
We deduce that
.
We deduce that 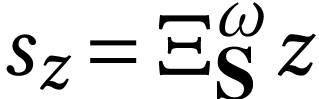 .
.
Otherwise, there is a number  and a sign
and a sign 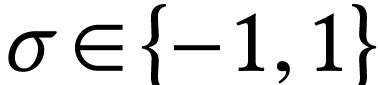 with
with 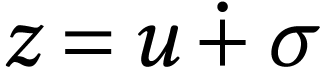 . Let
. Let
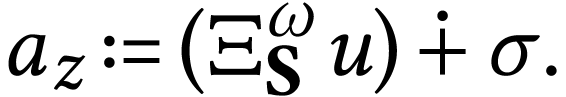
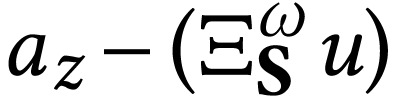 is
is  , the sign of
, the sign of  is
is  as well, so
as well, so  .
It follows by induction that
.
It follows by induction that 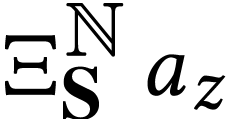 is a
is a 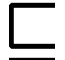 -chain whose supremum
-chain whose supremum 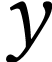 lies in each
lies in each  for
for 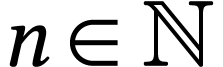 by
closure of those structures, so
by
closure of those structures, so  .
Since the sign of
.
Since the sign of 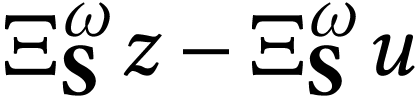 is
is  , we have
, we have 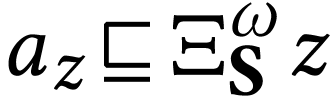 ,
whence
,
whence 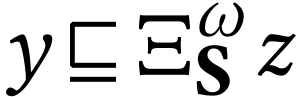 . Now
. Now 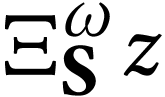 is the simplest
is the simplest 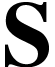 -fixed number
such that the sign of
-fixed number
such that the sign of 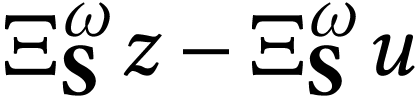 is
is  , whence
, whence 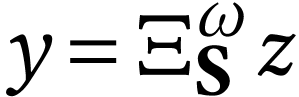 .
.

In this section, we define the exponential function of [9,
Chapter 10] as well as the surreal substructures  and
and 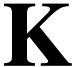 .
.
Inductive equationsRecall that by
Conway's construction, or in Gonshor's setting by [9,
Theorem 2.1], given sets 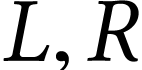 of numbers with
of numbers with 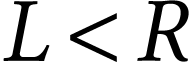 , there is a unique
, there is a unique  -minimal, or simplest, number
-minimal, or simplest, number 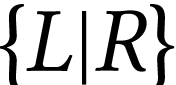 with
with
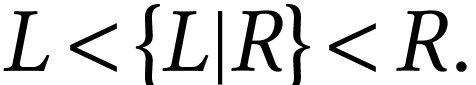
Let  be a surreal substructure. Carrying the
previous property through the parametrization of
be a surreal substructure. Carrying the
previous property through the parametrization of  , we obtain, given a surreal substructure
, we obtain, given a surreal substructure 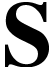 and subsets
and subsets 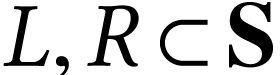 with
with 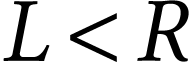 , a unique
, a unique  -minimal
element
-minimal
element 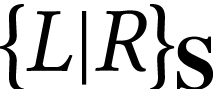 of
of  with
with
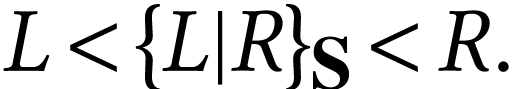
In order to write certain equations, we will write, for  ,
, 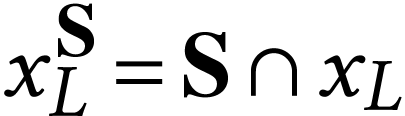 and
and 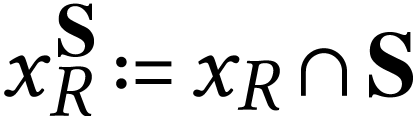 . Notice that we have
. Notice that we have 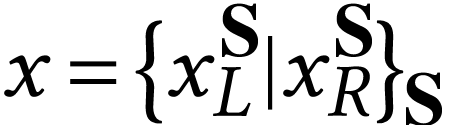 by definition. Thus if
by definition. Thus if  is another surreal
substructure, the surreal isomorphism
is another surreal
substructure, the surreal isomorphism  sends
sends 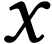 onto
onto
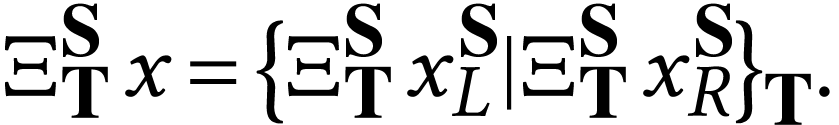 |
(1) |
Surreal exponentiation Gonshor uses an inductive
equation to define the exponential function. Given 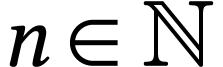 and
and  , set
, set
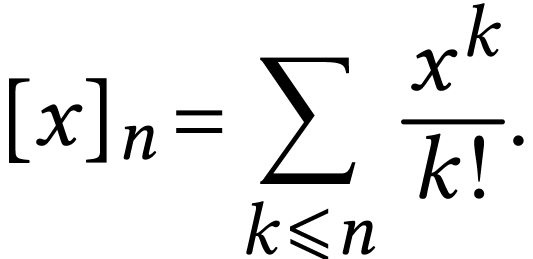
Let  be such that
be such that 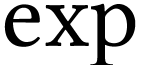 is
defined on
is
defined on 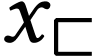 . Notice that for
instance, for
. Notice that for
instance, for  and
and 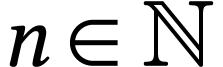 ,
we should have
,
we should have
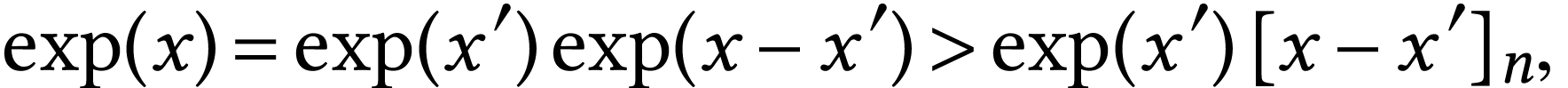
whereas similar inequalities hold for 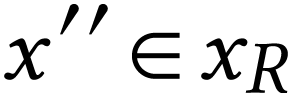 .
This led Gonshor to define
.
This led Gonshor to define
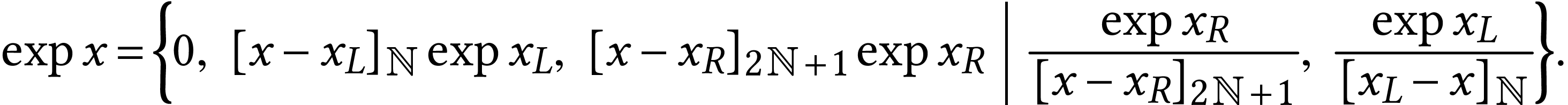
Gonshor proved that this equation is warranted and that it does define a
strictly increasing bijective morphism  .
We write
.
We write 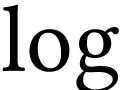 for the reciprocal of
for the reciprocal of 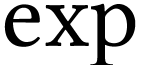 .
.
The functions 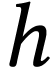 and
and 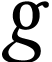 The function
The function 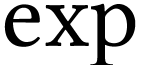 interacts with the
interacts with the
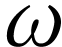 -map in the following way:
-map in the following way:
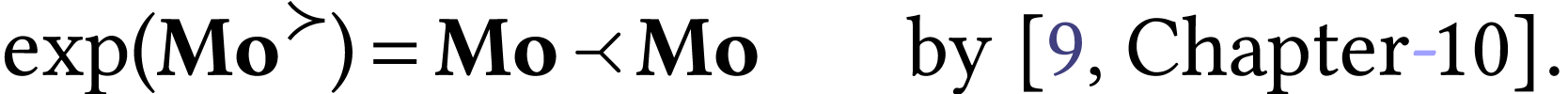
More precisely, for every strictly positive number 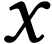 and every number
and every number 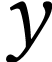 , we have
, we have
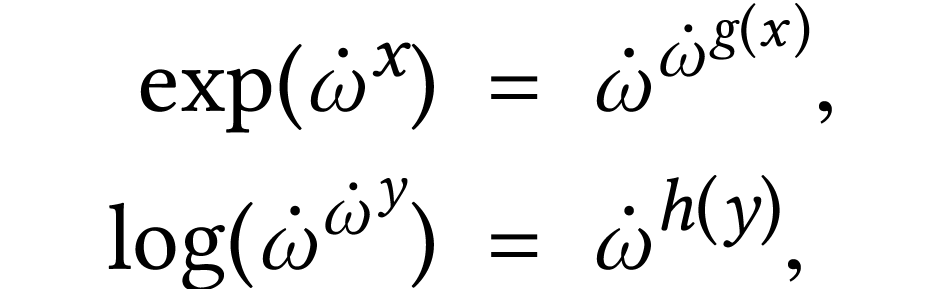
where the strictly increasing and bijective function 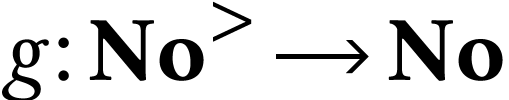 and its reciprocal
and its reciprocal 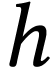 have the following equations
in
have the following equations
in  and
and  [9,
Theorems 10.11 and 10.12]:
[9,
Theorems 10.11 and 10.12]:
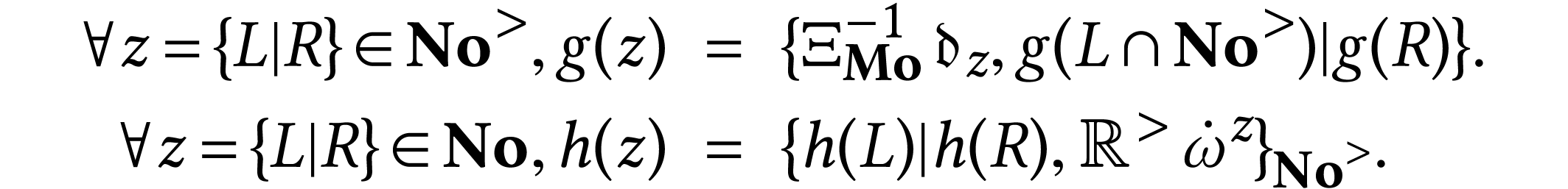
The function 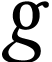 was entirely studied by Gonshor who
gave formal results such as the characterization of its fixed points and
as well as a somewhat informal description of the sign sequence of
was entirely studied by Gonshor who
gave formal results such as the characterization of its fixed points and
as well as a somewhat informal description of the sign sequence of 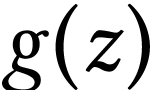 for any strictly positive number
for any strictly positive number 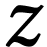 given that of
given that of 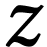 . We will
recover part of his results in a different approach in Section 4.
. We will
recover part of his results in a different approach in Section 4.
The class  of log-atomic numbers is defined as
the class of numbers
of log-atomic numbers is defined as
the class of numbers 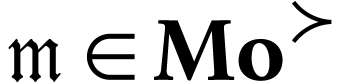 with
with 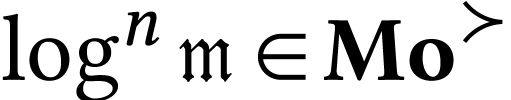 for all
for all 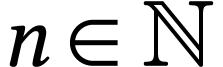 . In other words, we
have the equality
. In other words, we
have the equality
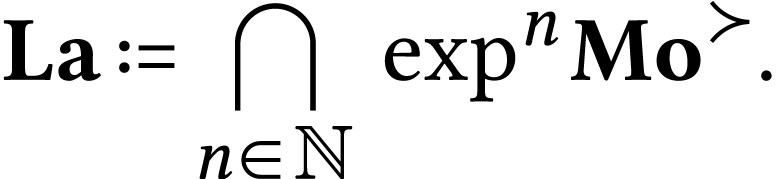
The class  was first described by Berarducci and
Mantova [5] in order to define a derivation on
was first described by Berarducci and
Mantova [5] in order to define a derivation on  . We next describe the parametrization of
. We next describe the parametrization of  .
.
Consider, for 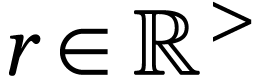 and
and 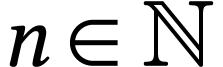 the
function
the
function
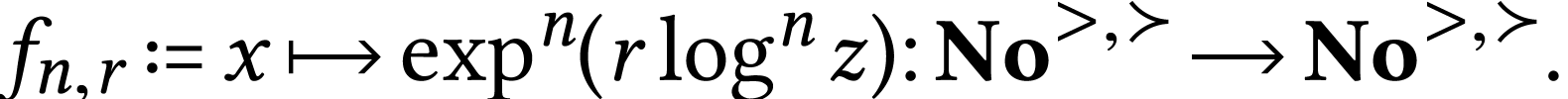
Recall that the class of monomials is that of numbers 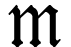 which are simplest in each class
which are simplest in each class
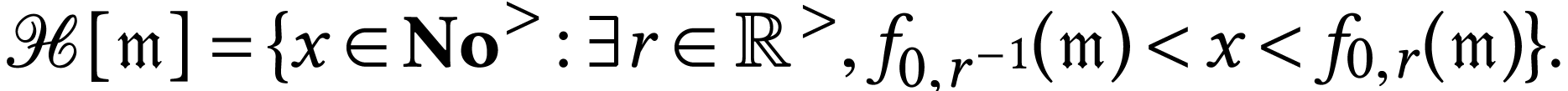
Similarly, Berarducci and Mantova proved that log-atomic numbers 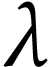 are exactly the simplest numbers of each class
are exactly the simplest numbers of each class
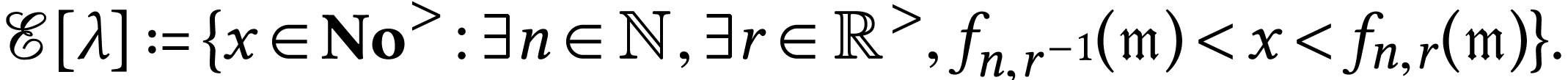
Moreover, they derived [5, Definition 5.12 and Corollary
5.17] the following equation for the parametrization 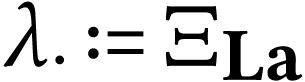 of
of  :
:
where 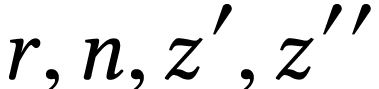 respectively range in
respectively range in  ,
,  ,
,
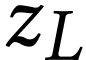 and
and 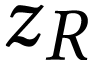 .
.
Moreover, the following formula [2, Proposition 2.5] is
know for 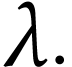 :
:
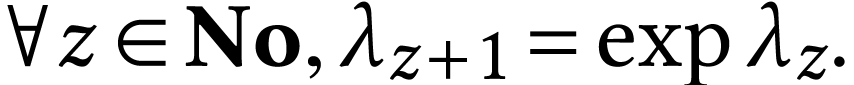 |
(3) |
In [4], we defined a strictly increasing bijection 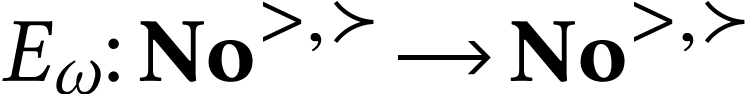 which satisfies the equation
which satisfies the equation
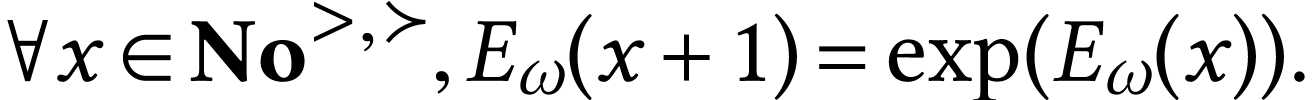 |
(4) |
Morever, this function is surreal-analytic at every point in the sense
of [6, Definition 7.8] and satisfies 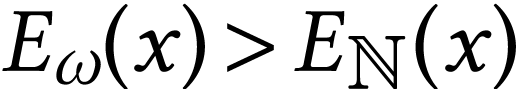 for all
for all  . This function can
be seen as a surreal counterpart to Kneser's transexponential function
[12].
. This function can
be seen as a surreal counterpart to Kneser's transexponential function
[12].
In order to define 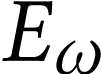 , we
relied on a surreal substructure
, we
relied on a surreal substructure  of so-called
truncated numbers. They can be characterized as numbers
of so-called
truncated numbers. They can be characterized as numbers  with
with 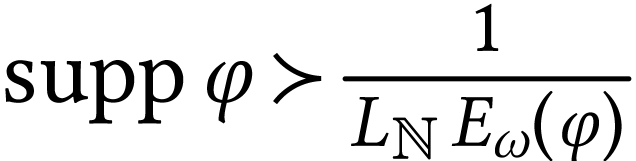 . The function
. The function 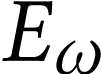 is defined on the class of truncated series by the
equation:
is defined on the class of truncated series by the
equation:
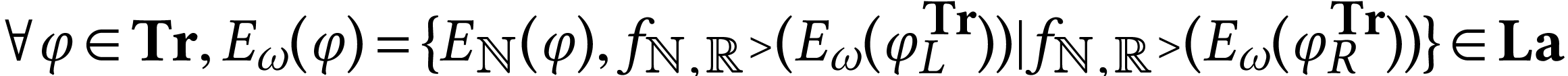
This equation realizes a strictly increasing bijection 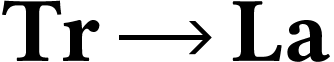 .
.
Now consider the set 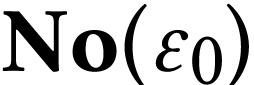 of surreal numbers
of surreal numbers 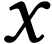 with length
with length 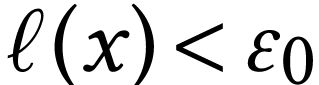 .
By [8, Corollary 5.5], the structure
.
By [8, Corollary 5.5], the structure 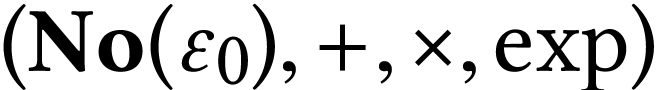 is an elementary extension of the real exponential field. Moreover, for
is an elementary extension of the real exponential field. Moreover, for
 , there is
, there is 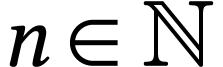 with
with 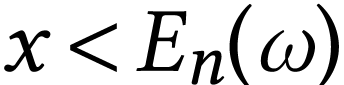 . It follows that each
element of
. It follows that each
element of  is truncated, and that for
is truncated, and that for 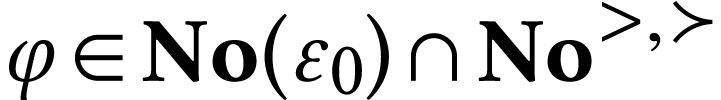 , the sets
, the sets 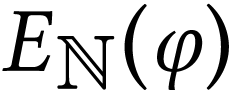 and
and 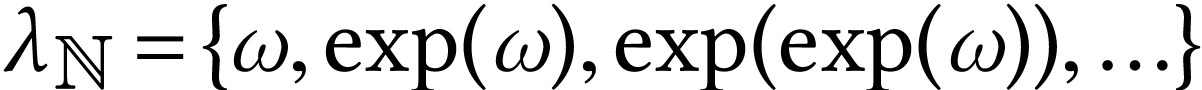 are mutually cofinal with respect to one
another. Thus on
are mutually cofinal with respect to one
another. Thus on 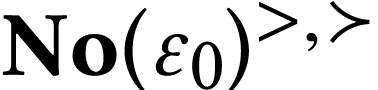 , the
equation for
, the
equation for 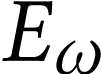 becomes
becomes
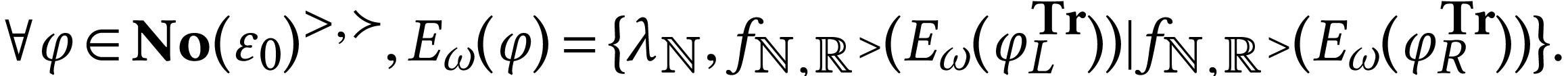
We claim that 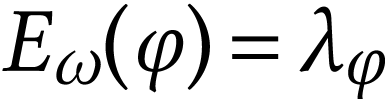 for all
for all  . We prove this by induction on
. We prove this by induction on 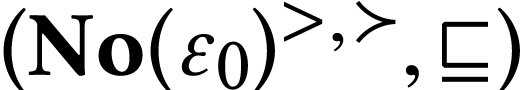 . Let
. Let 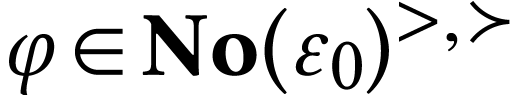 such that the
result holds on
such that the
result holds on 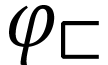 . Noticing
that
. Noticing
that 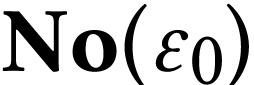 is
is  -initial
in
-initial
in  , we get
, we get
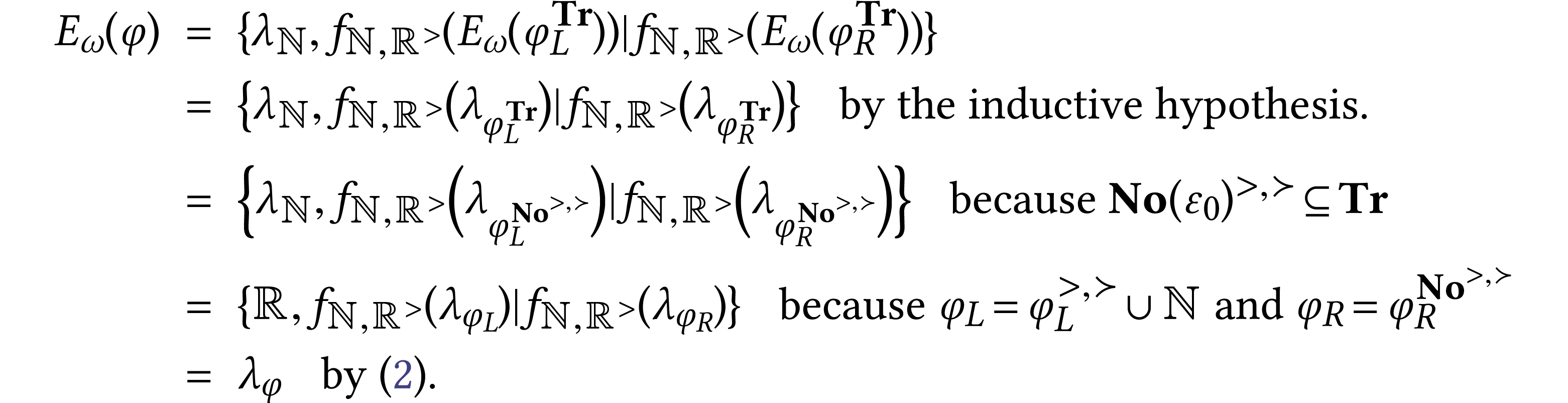
So 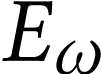 and
and 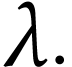 coincide on
coincide on  .
.
The structure 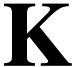 of
of  -numbers was introduced first and studied in
detail by S. Kuhlmann and M. Matusinski in [13]. It was
designed as an intermediate subclass between fundamental monomials and
log-atomic numbers. The relation between
-numbers was introduced first and studied in
detail by S. Kuhlmann and M. Matusinski in [13]. It was
designed as an intermediate subclass between fundamental monomials and
log-atomic numbers. The relation between 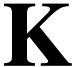 and
and 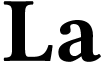 is given by the imbrication
is given by the imbrication
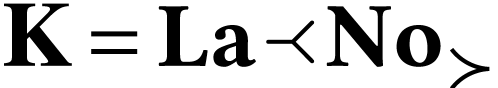 of [14, p 21].
of [14, p 21].
Similarly to monomials and log-atomic numbers, 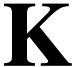 numbers can be characterized as simplest elements in each convex class
numbers can be characterized as simplest elements in each convex class
The parametrization 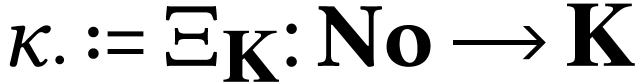 of
of  is given by the equation
is given by the equation
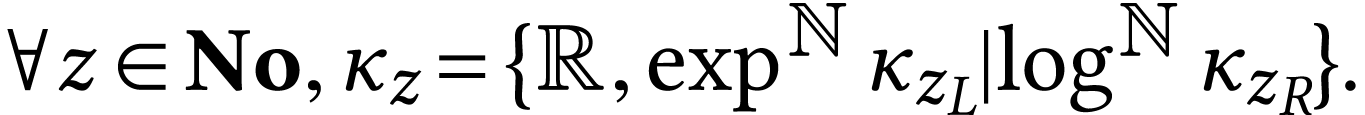
Moreover, by [3, Corollary 13 and Theorem 6.16], the
structure  is closed.
is closed.
In order to compute the sign sequence of  -numbers,
Kuhlmann and Matusinski rely on an intermediate surreal substructure
denoted
-numbers,
Kuhlmann and Matusinski rely on an intermediate surreal substructure
denoted 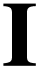 . This surreal substructure is
defined by the imbrication relation:
. This surreal substructure is
defined by the imbrication relation: 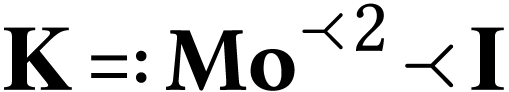 .
Indeed, since
.
Indeed, since 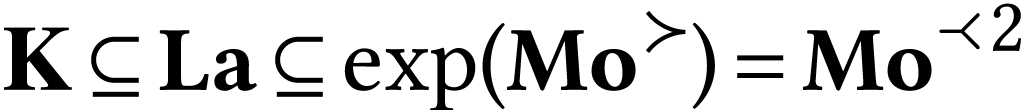 , the structure
, the structure
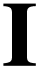 exists and is unique.
exists and is unique.
For  we let
we let 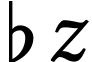 denote the
number with
denote the
number with 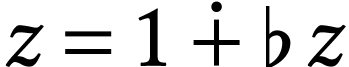 if
if 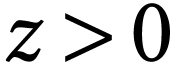 and
and 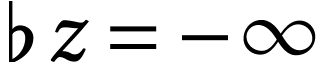 if
if 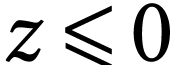 . We
also extend the functions
. We
also extend the functions 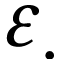 and
and  to
to  with
with 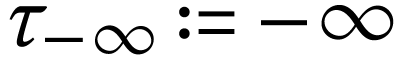 and
and 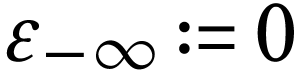 . For
. For  ,
we define
,
we define 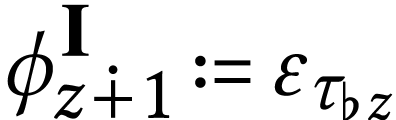 and
and 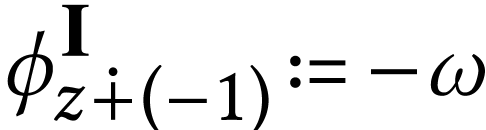 .
The parametrization
.
The parametrization 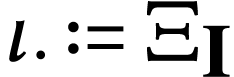 of
of 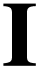 admits the following sign sequence formula
admits the following sign sequence formula
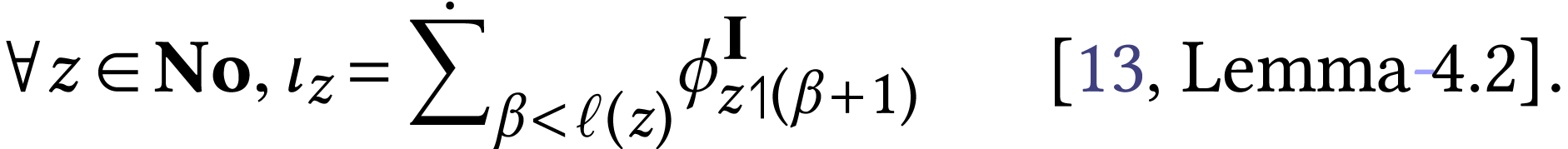
Our goal is to compute the sign sequence of 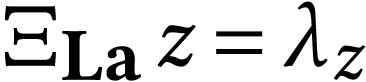 in
terms of that of
in
terms of that of 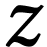 , for all
numbers
, for all
numbers 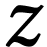 . Recall that
. Recall that 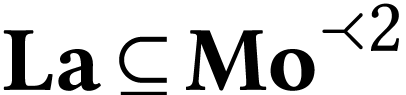 , so there is a surreal
substructure
, so there is a surreal
substructure  with
with  .
We write
.
We write 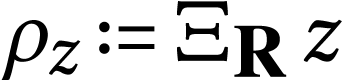 for all
for all  . We have
. We have 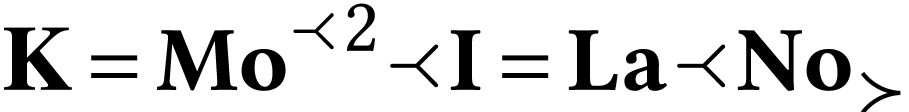 ,
whence
,
whence 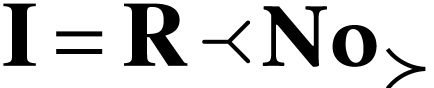 . The computation in
[13] of sign sequences of numbers in
. The computation in
[13] of sign sequences of numbers in 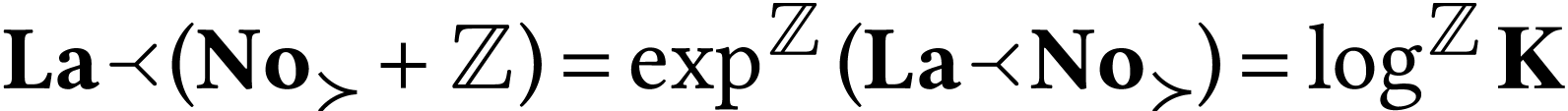 can thus be used to derive part of the result.
can thus be used to derive part of the result.
For 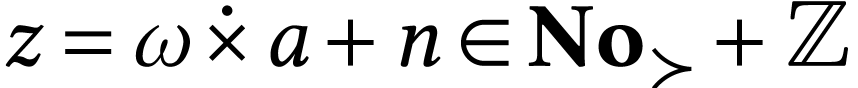 where
where  and
and  , we have
, we have 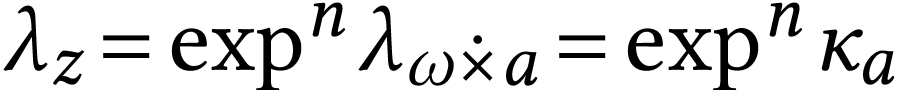 . By [13, Theorem 4.3], we have
. By [13, Theorem 4.3], we have
Our goal is to extend this description to the sign sequences of numbers
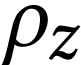 for all
for all  ,
relying on the known values
,
relying on the known values 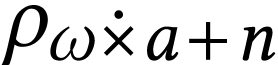 for all
for all  and
and  . More
precisely, we will compute
. More
precisely, we will compute  on all intervals
on all intervals
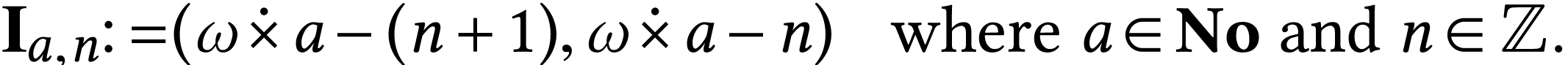
Since  can be realized as the reunion
can be realized as the reunion
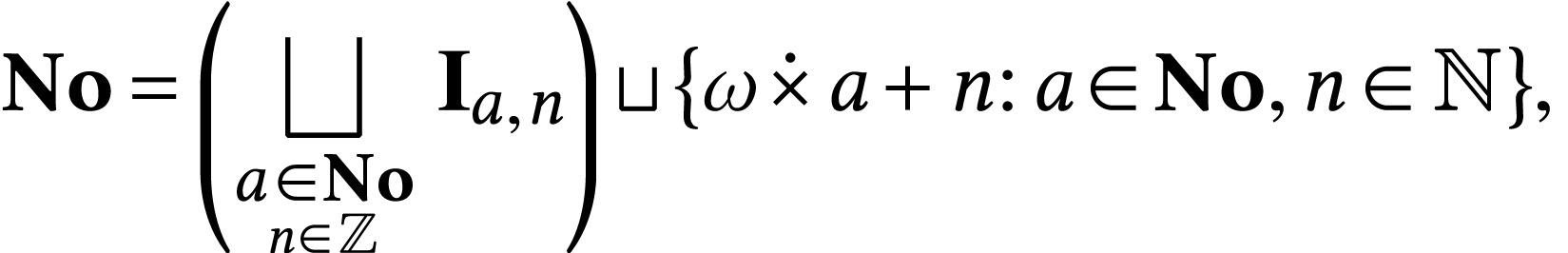
this will cover all cases. The sign sequence of 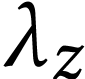 can then be computed using Proposition 4 twice. In order to
compute the sign sequence for
can then be computed using Proposition 4 twice. In order to
compute the sign sequence for  ,
we first describe the action of
,
we first describe the action of 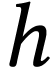 and
and 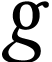 on sign sequences in certain cases.
on sign sequences in certain cases.
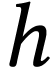
Let  be fixed and write
be fixed and write 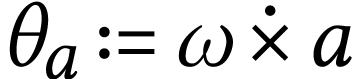 .
.
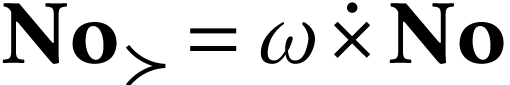 and [13, Lemma 4.2]. The
second immediately follows.
and [13, Lemma 4.2]. The
second immediately follows.

Recall that we have 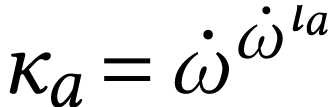 so
so 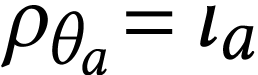 . By [13, Lemma 4.2], we have
. By [13, Lemma 4.2], we have 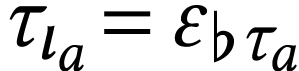 . We set
. We set
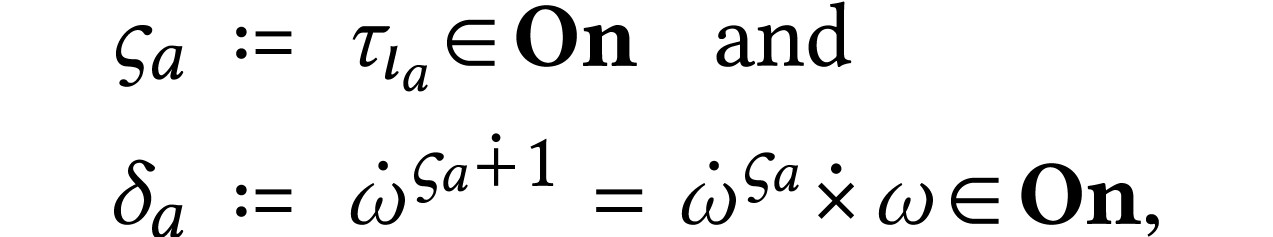
so 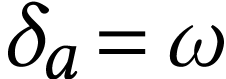 if
if 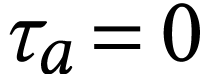 and
and  if
if 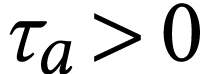 . We will
treat the cases
. We will
treat the cases 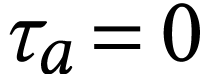 and
and 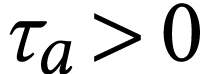 in a
uniform way.
in a
uniform way.
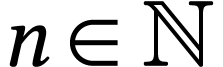 , we have
, we have 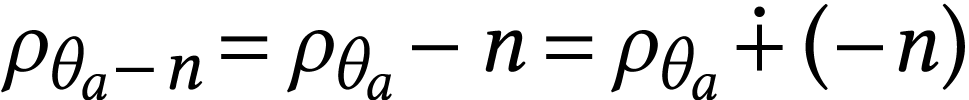
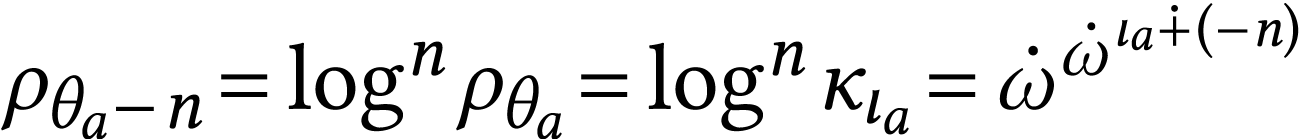 by [13, Theorem 4.3(1)]. By Lemma 20, we have
by [13, Theorem 4.3(1)]. By Lemma 20, we have  so
so 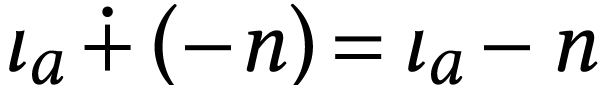 , so
, so
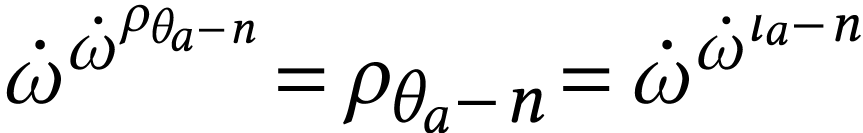 . Since
. Since 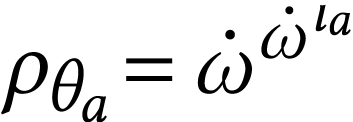 , we have
, we have 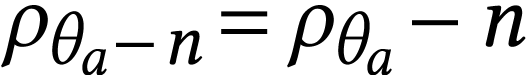 .
It follows that
.
It follows that 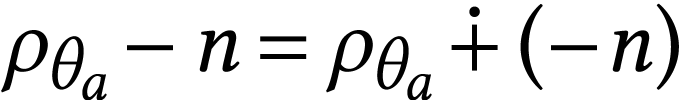 .
.

We now fix  and we set
and we set 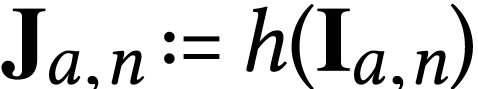 . By the previous lemma, we can write the interval
. By the previous lemma, we can write the interval
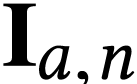 as the surreal substructure
as the surreal substructure
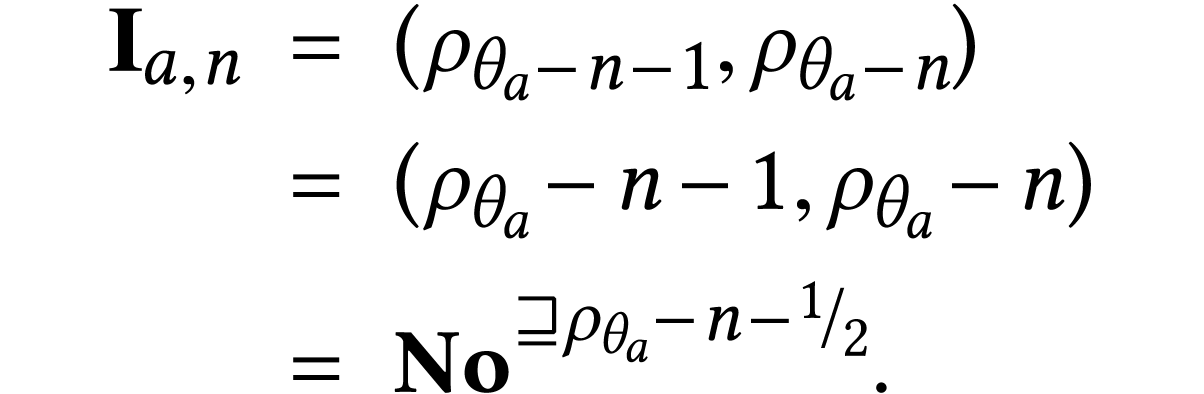
Thus 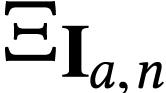 is straightforward to compute in terms of
sign sequences.
is straightforward to compute in terms of
sign sequences.
We have 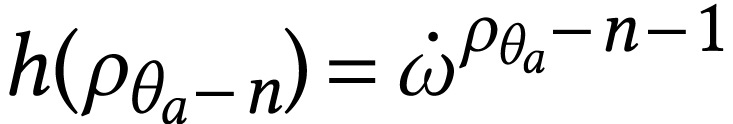 and
and 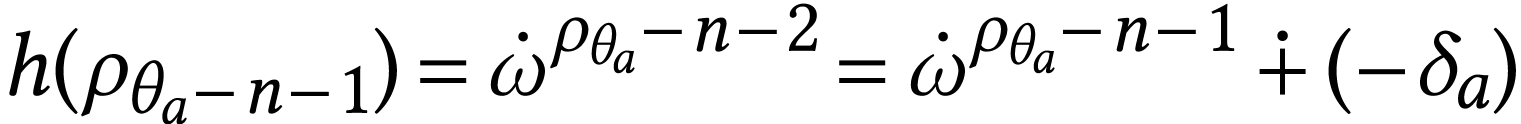 .
Thus the interval
.
Thus the interval 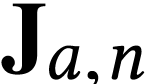 is subject to the computation
given in Lemma 9(b). That is, we have:
is subject to the computation
given in Lemma 9(b). That is, we have:
 , we have
, we have
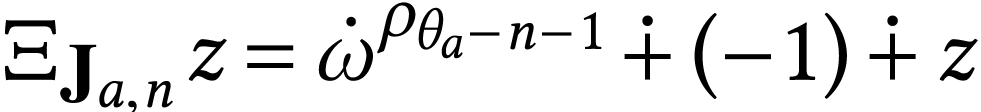 if
if 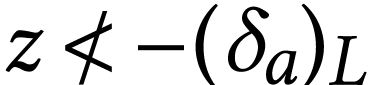 .
.
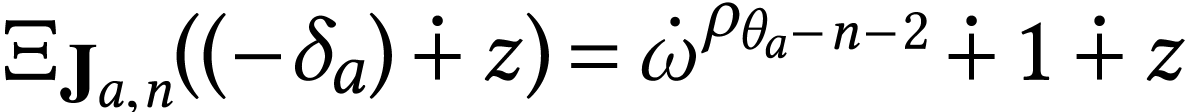 .
.
Moreover, for 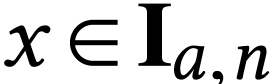 , we have
, we have 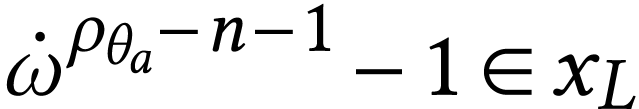 and
and 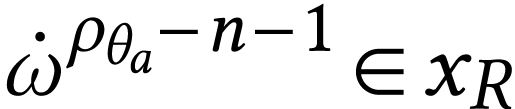 . This
implies that
. This
implies that 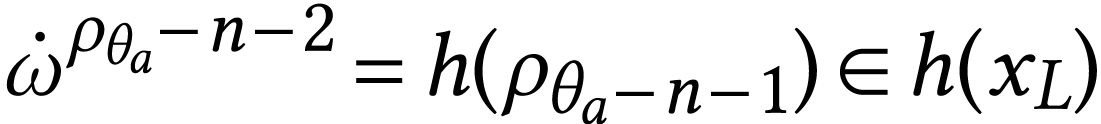 and that
and that 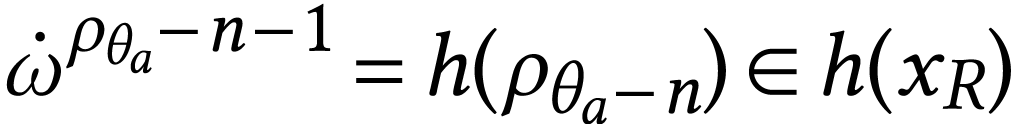 . Since with
. Since with 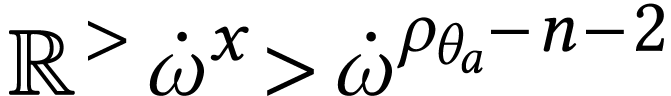 ,
we deduce the following equation for
,
we deduce the following equation for 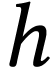 on
on 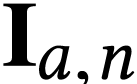 :
:
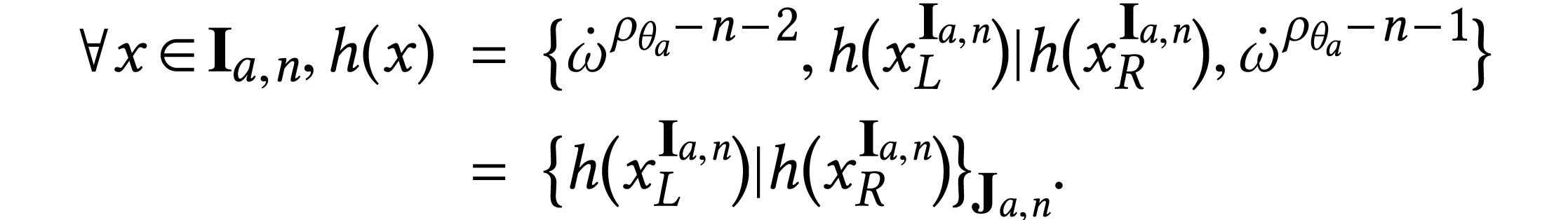
We see that 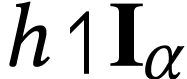 is the surreal isomorphism
is the surreal isomorphism 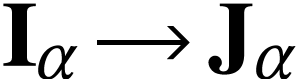 , so
, so  .
.
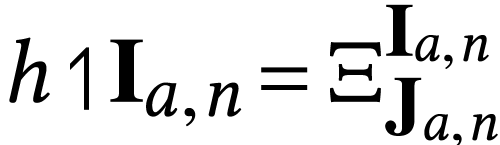 .
.

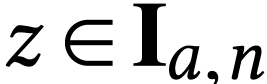 , if the number
, if the number 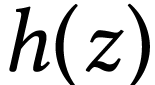 is a monomial, then there is
is a monomial, then there is  with
with
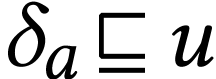 and
and 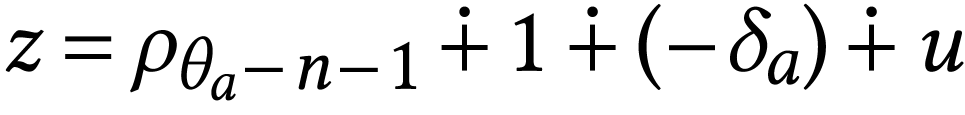 .
.
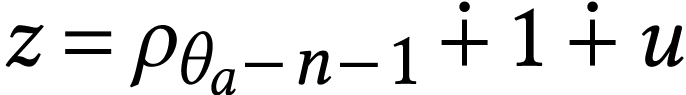 where
where 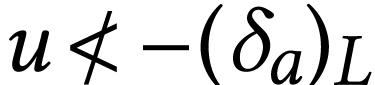 . Since
. Since 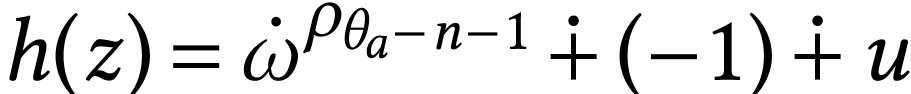 is
a monomial with
is
a monomial with 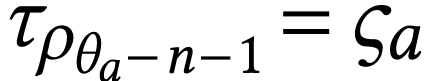 , by
Proposition 4, the sign sequence of
, by
Proposition 4, the sign sequence of  must start with
must start with 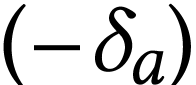 , which
contradicts the hypothesis on
, which
contradicts the hypothesis on  .
We deduce that there is a number
.
We deduce that there is a number  with
with 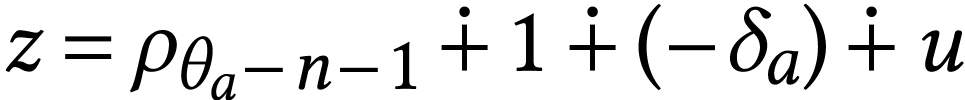 . Since
. Since 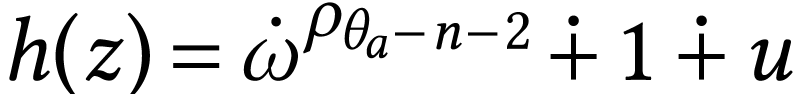 is
a monomial and by the same argument, the sign sequence of
is
a monomial and by the same argument, the sign sequence of  must start with at least
must start with at least 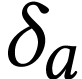 many
signs
many
signs 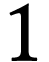 , that is, we must have
, that is, we must have
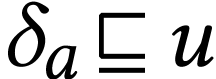 .
.

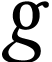
For 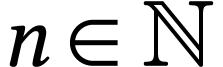 , we set
, we set
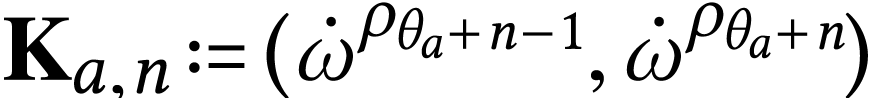
and
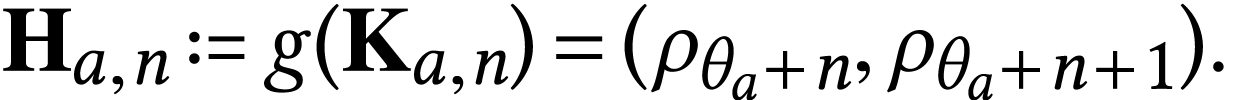
Recall that if 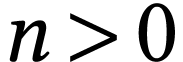 , we have
, we have
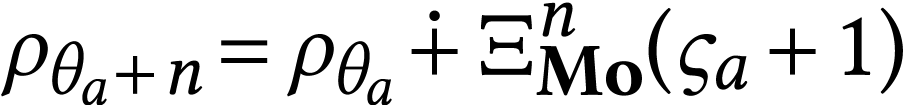 , so
, so 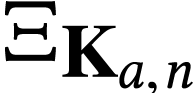 is subject to the computations of Lemma 9(a).
We have
is subject to the computations of Lemma 9(a).
We have 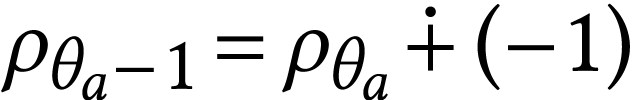 , so
, so 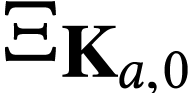 is subject to the computations of Lemma 9(b),
whence
is subject to the computations of Lemma 9(b),
whence
 , and
, and 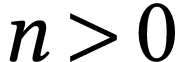 ,
we have
,
we have
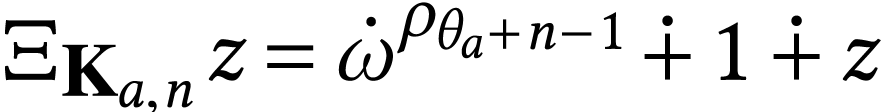 if
if 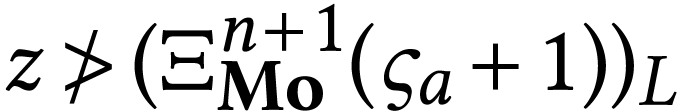 .
.
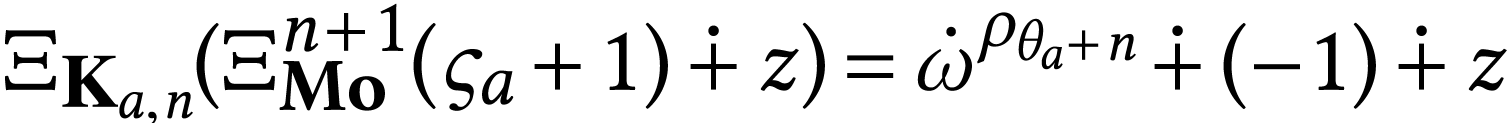 if
if 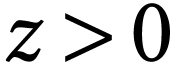 .
.
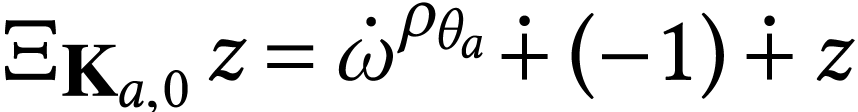 if
if 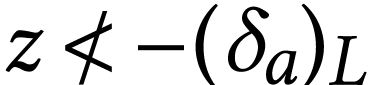 .
.
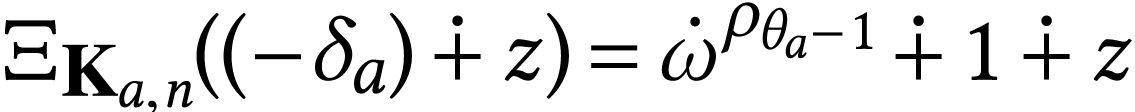 if
if 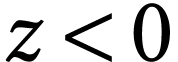 .
.
 and
and 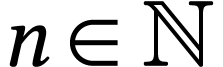 we have
we have
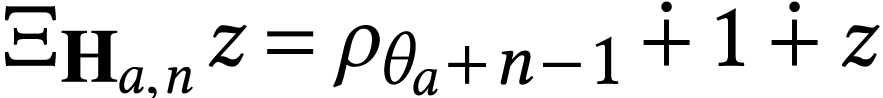 if
if 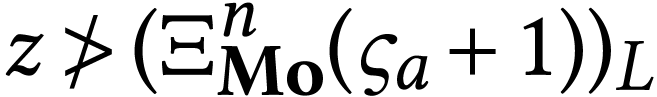 .
.
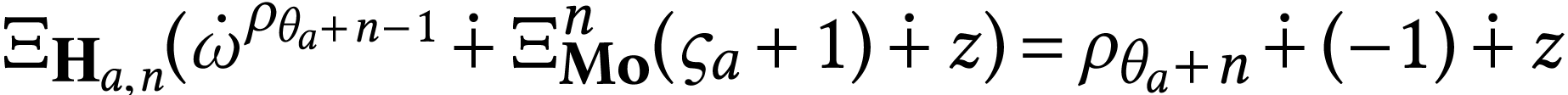 if
if 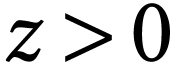 .
.

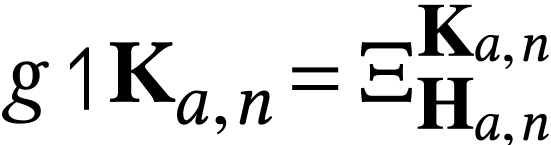 .
.
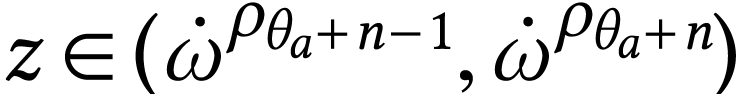 .
We have
.
We have 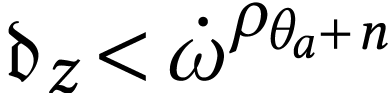 so
so 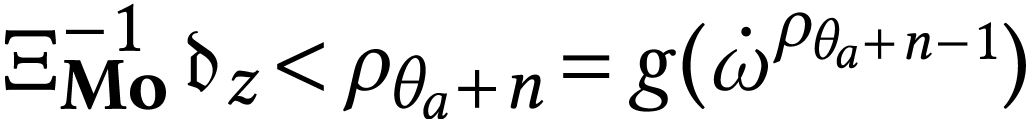 .
We now compute
.
We now compute
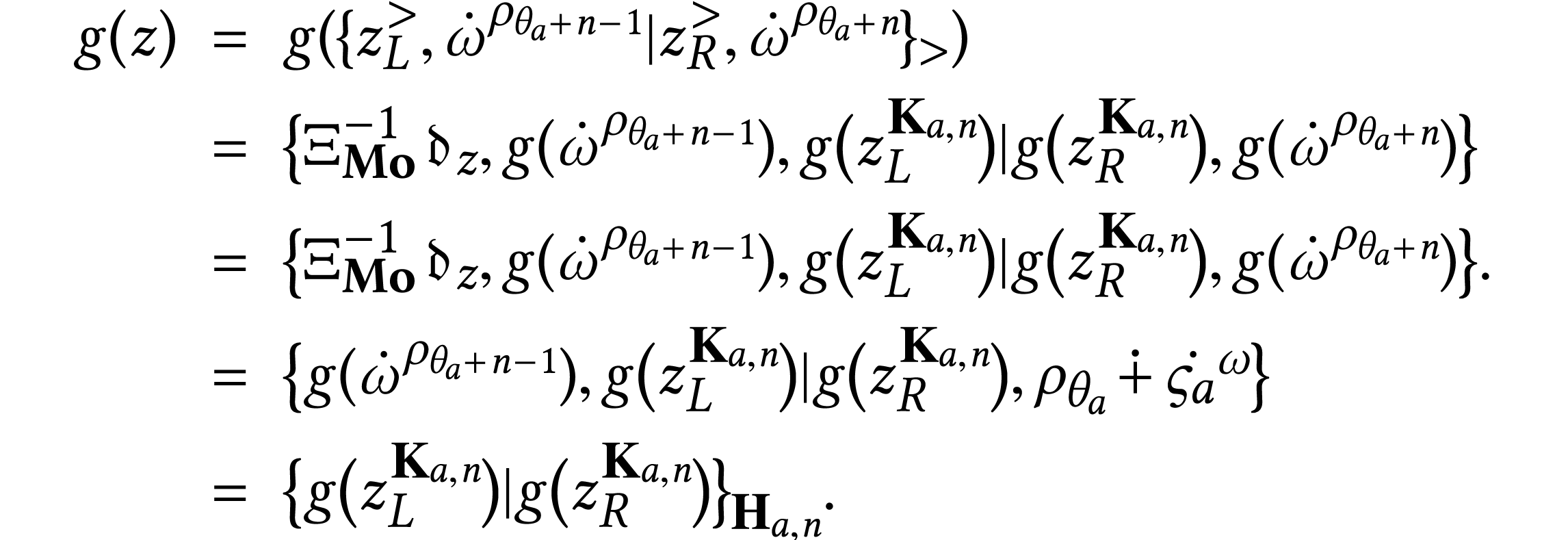
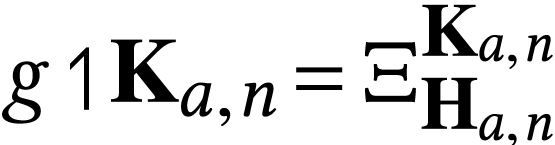 .
.

 , and
, and 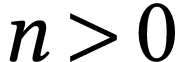 , we have
, we have

Piecing the descriptions of Propositions 23 and 28
together, one obtains a full description of the sign sequence of 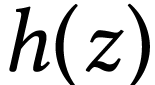 for
for  . We
will only require part of those descriptions to reach our goal of
describing sign sequences in
. We
will only require part of those descriptions to reach our goal of
describing sign sequences in  .
For
.
For  , we set
, we set 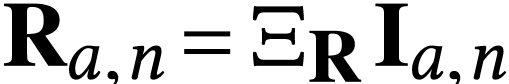 . We will characterize
. We will characterize 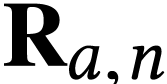 using fixed points of the surreal substructure
using fixed points of the surreal substructure
Notice that this structure depends only on  .
Both
.
Both  and
and 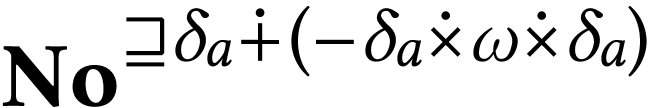 are closed so
are closed so
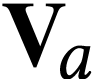 is closed by Lemma 15, so the class
is closed by Lemma 15, so the class
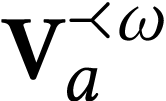 is also closed.
is also closed.
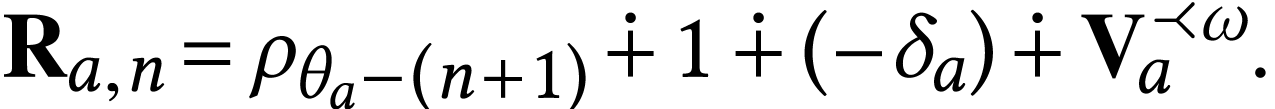
For 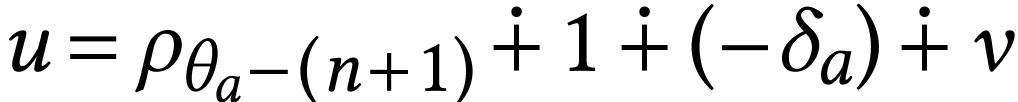 where
where 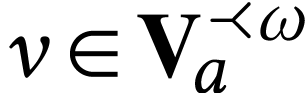 and
and
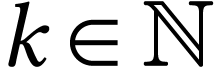 , we have
, we have
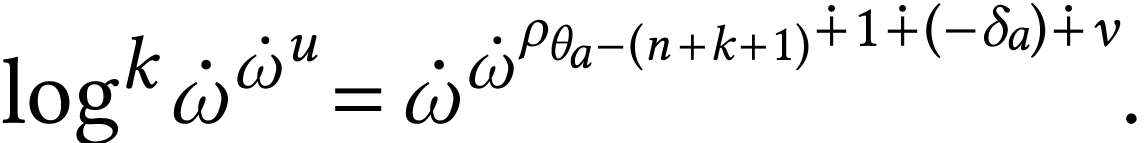
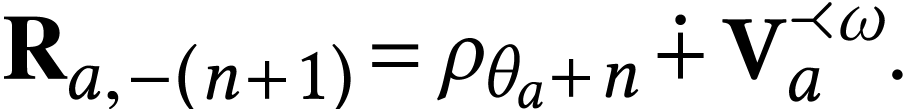
For 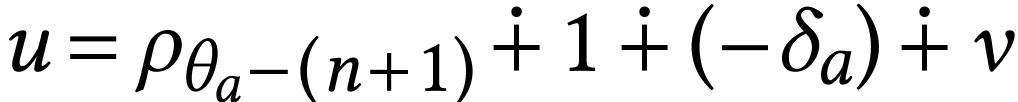 where
where 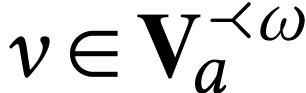 and
and
 , we have
, we have
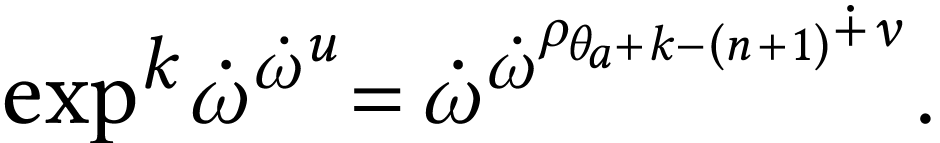
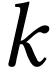 that we have
that we have
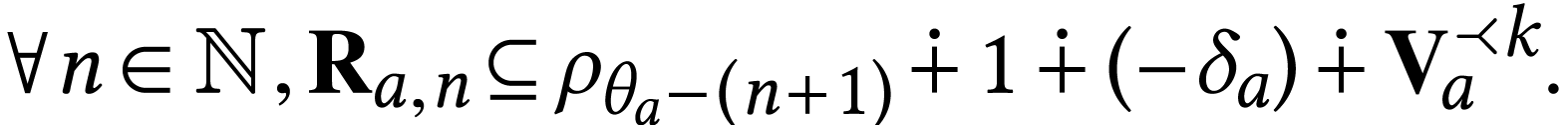
First assume that 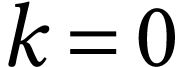 . For
. For 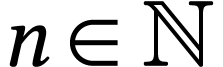 and
and  , the
number
, the
number 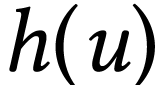 is a monomial, which implies by Lemma 24 that
is a monomial, which implies by Lemma 24 that  has the form
has the form 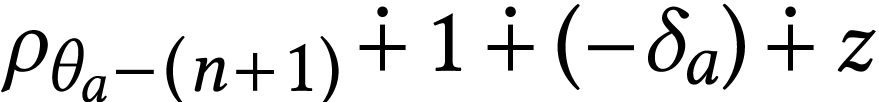 with
with 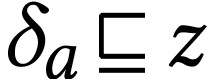 . This implies in
particular that
. This implies in
particular that 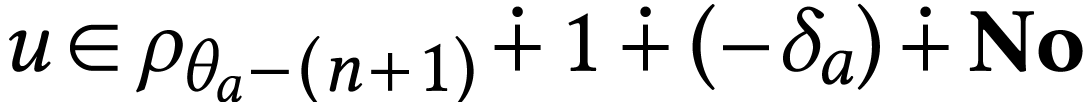 .
.
Let 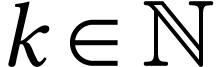 such that the result holds at
such that the result holds at 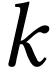 and consider
and consider 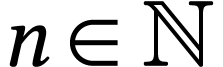 and
and 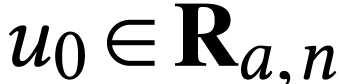 . There is a
. There is a  with
with 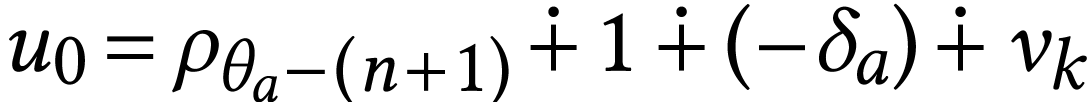 . Since
. Since 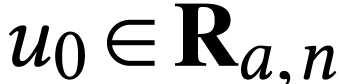 , we have
, we have 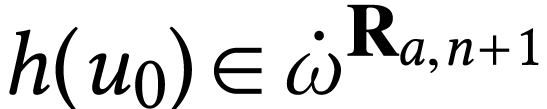 .
Now
.
Now 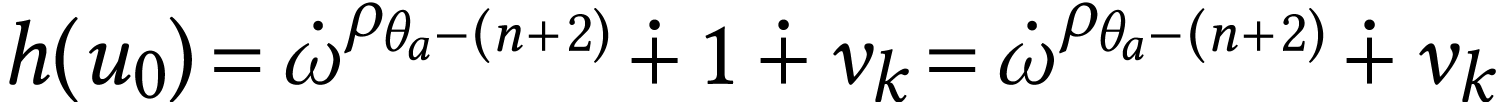 by Proposition 23(b).
Let
by Proposition 23(b).
Let 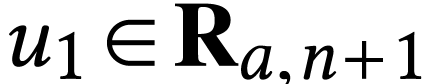 with
with 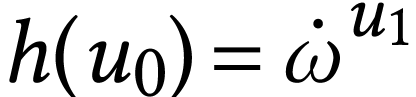 .
We have
.
We have 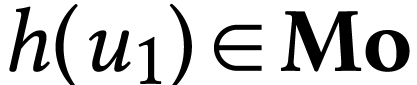 , so by Lemma 24, there is a number
, so by Lemma 24, there is a number 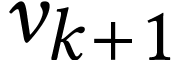 with
with 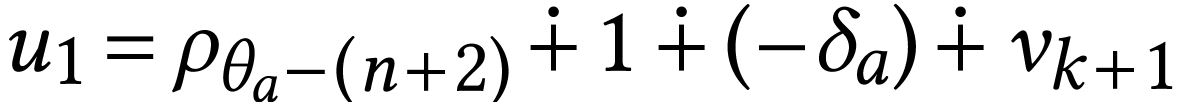 and
and 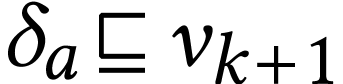 . Thus
. Thus
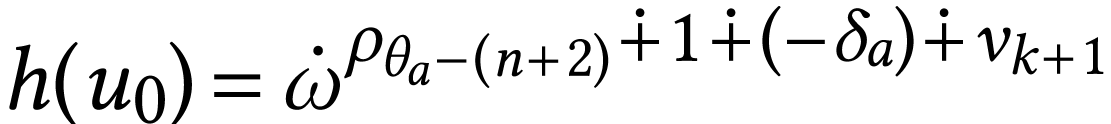 . By Proposition 4
and Lemma 5, we have
. By Proposition 4
and Lemma 5, we have
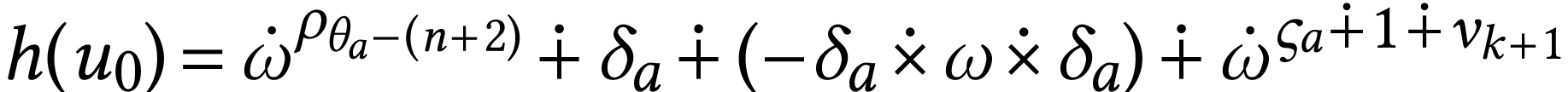
We identify
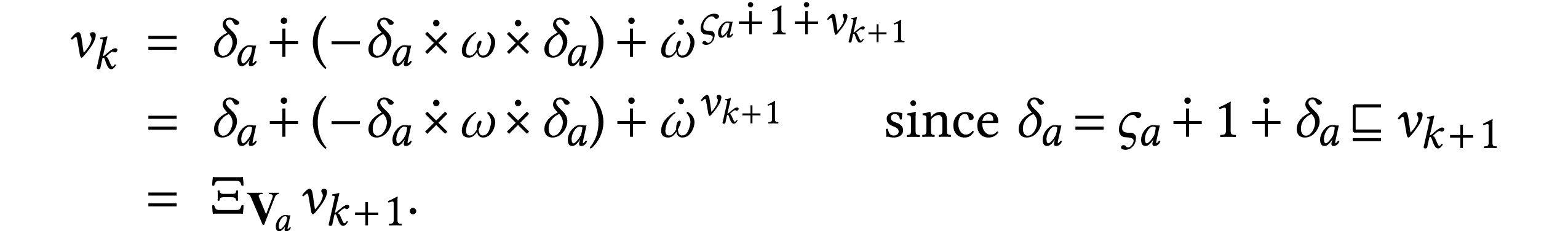
The inductive hypothesis applied at 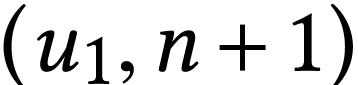 yields
yields 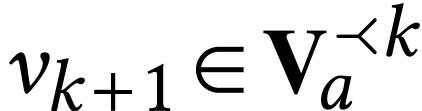 , so
, so 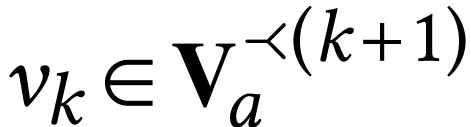 .
We thus have
.
We thus have
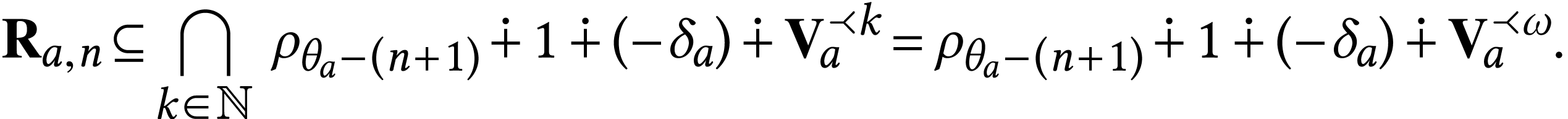
We next prove 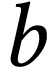 ). Since it
implies that
). Since it
implies that  , this will
yield
, this will
yield  ). We prove
). We prove 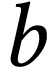 ) by induction on
) by induction on 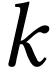 . Note that the result is immediate for
. Note that the result is immediate for 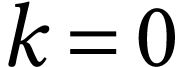 . Let
. Let 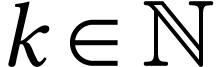 be
such that the formula holds at
be
such that the formula holds at 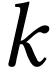 ,
let
,
let 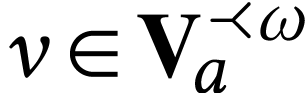 and consider
and consider 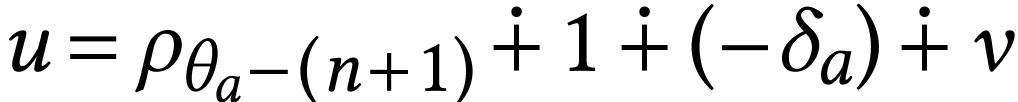 .
Our inductive hypothesis is
.
Our inductive hypothesis is
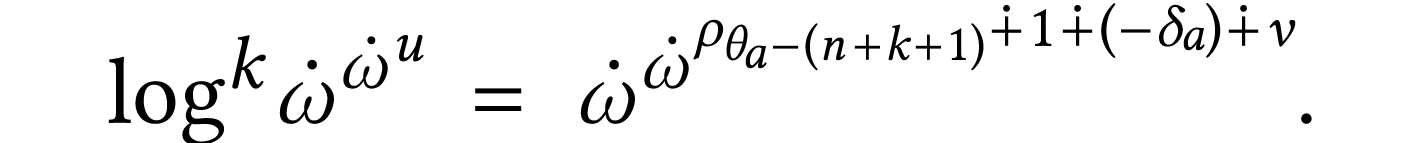
Thus
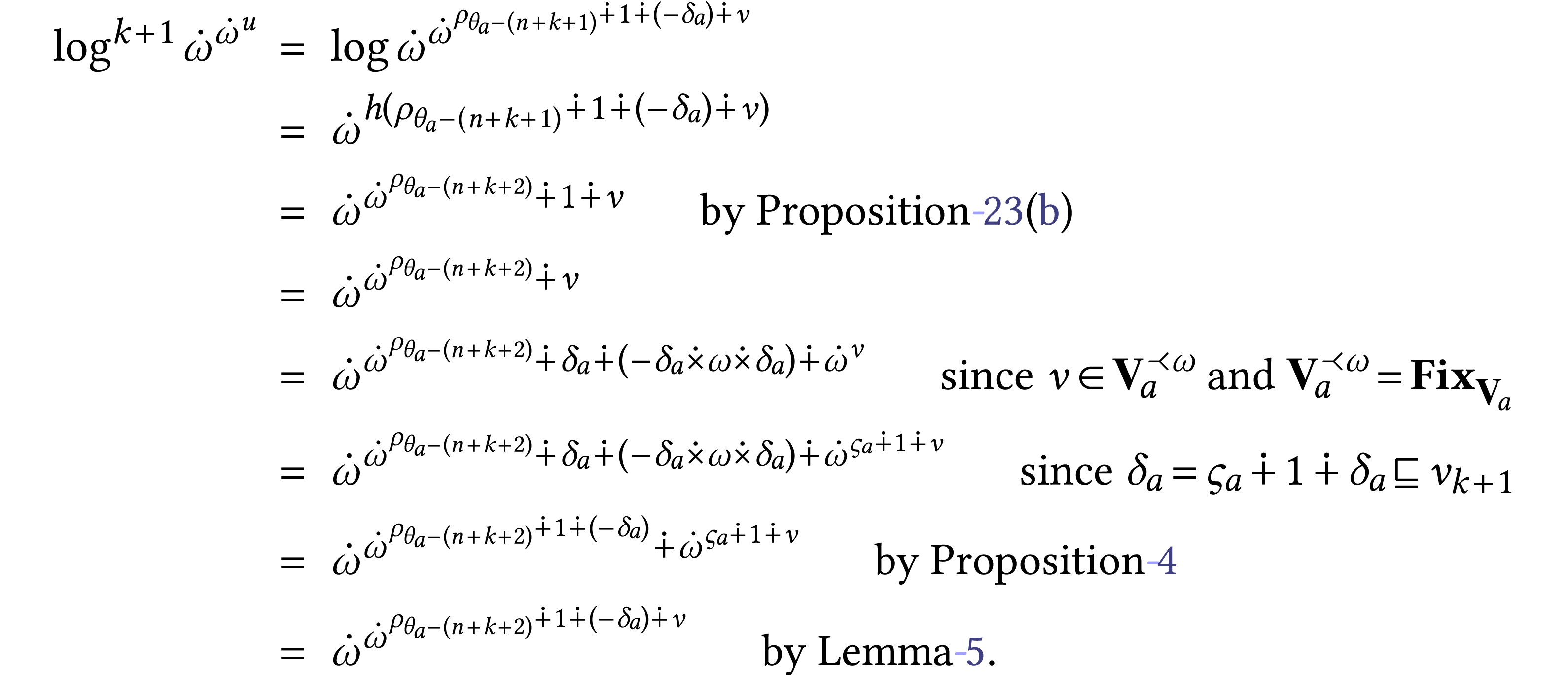
This are the desired results. The formula follows by induction.
We next prove 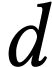 ). Let
). Let 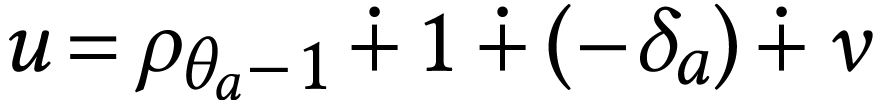 where
where 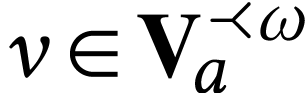 , so
that
, so
that  is a generic element of
is a generic element of 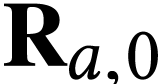 . By the same computations as above, we have
. By the same computations as above, we have
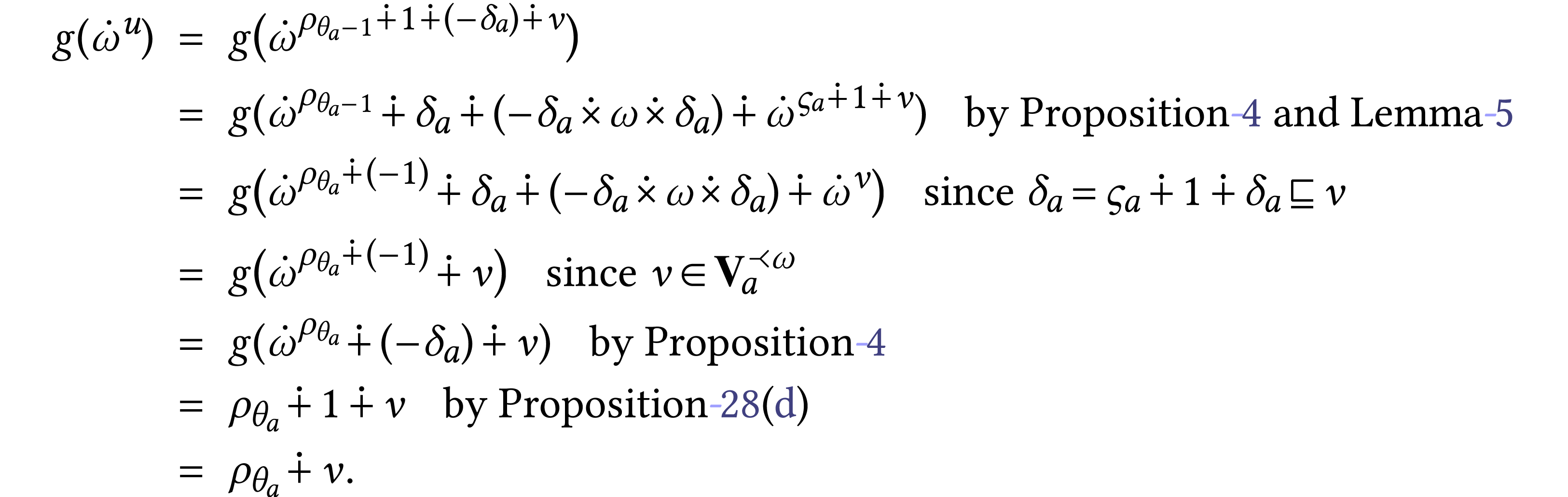
This proves the formula for 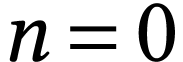 .
Now let
.
Now let 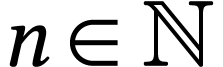 be such that the formula holds at
be such that the formula holds at 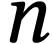 . Let
. Let 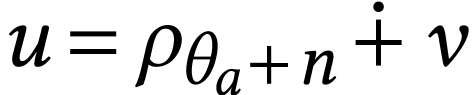 with
with
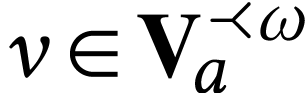 be a generic element of
be a generic element of 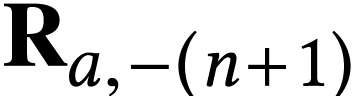 . We have
. We have 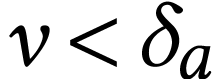 so
so 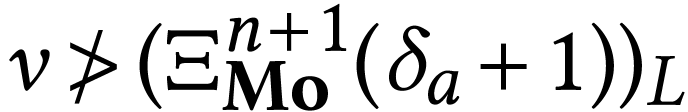 , thus Proposition 28(a)
yields
, thus Proposition 28(a)
yields
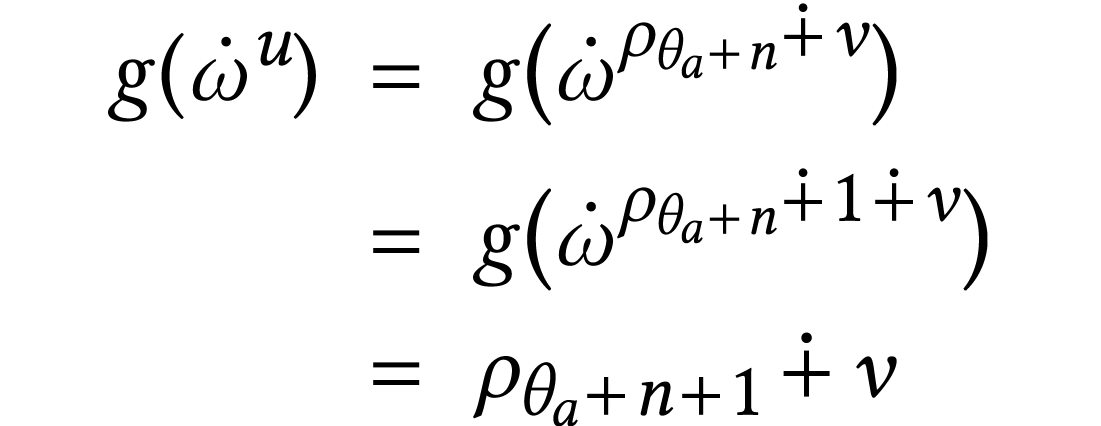
 is true for all
is true for all
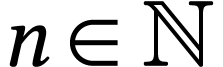 .
.

 , the structure
, the structure 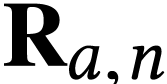 is closed.
is closed.
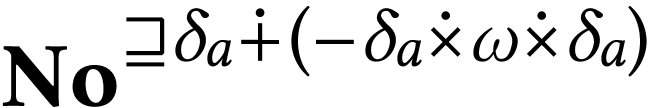 and
and 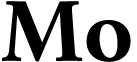 are closed and by Lemma 15, the surreal
substructure
are closed and by Lemma 15, the surreal
substructure 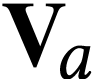 is closed. Therefore
is closed. Therefore 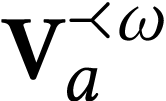 is closed. By the previous theorem, the structure
is closed. By the previous theorem, the structure 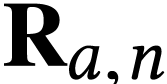 can be expressed as
can be expressed as 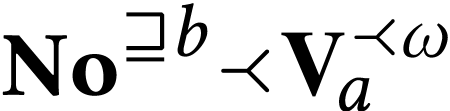 for a
certain number
for a
certain number 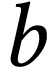 depending on
depending on  and
and 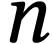 . So by Lemma 15,
it is closed.
. So by Lemma 15,
it is closed.

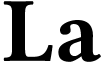 is closed.
is closed.
 be a non-empty
chain in
be a non-empty
chain in  . We want to prove
that
. We want to prove
that 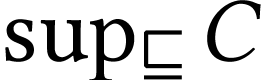 is log-atomic. We may assume that
is log-atomic. We may assume that  has no
has no  -maximum.
-maximum.
If the set  of
of  -numbers
-numbers
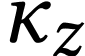 with
with 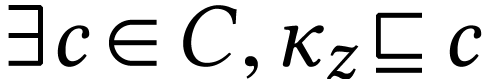 is
is  -cofinal in
-cofinal in  ,
then
,
then  by closure of
by closure of 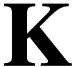 ,
so
,
so 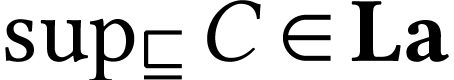 .
.
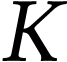 is not
is not 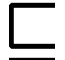 -cofinal
in
-cofinal
in  . Let
. Let 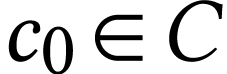 be
be 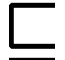 -minimal with
-minimal with 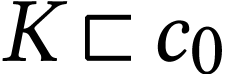 . Let
. Let 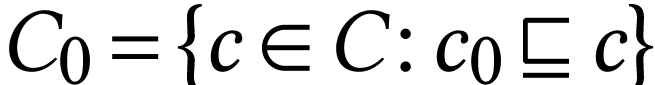 and notice that
and notice that
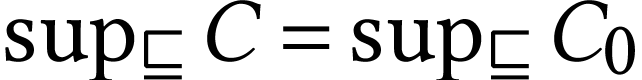 . Let
. Let  with
with 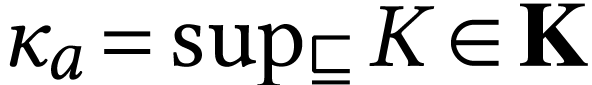 . For
. For 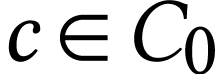 , the number
, the number 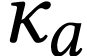 is
is 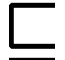 -maximal in
-maximal in 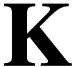 with
with 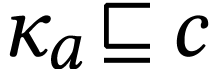 . By [3,
Corollary 7.13 and Theorem 6.16], we have
. By [3,
Corollary 7.13 and Theorem 6.16], we have  for
all
for
all 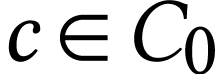 , whence
, whence 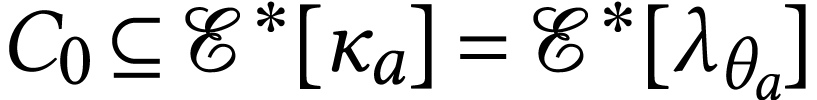 . The set
. The set 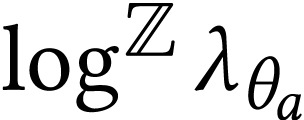 is cofinal
and coinitial in
is cofinal
and coinitial in 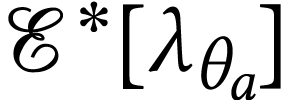 for the order
for the order 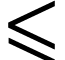 . So for each element
. So for each element 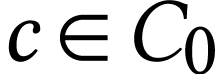 there is a unique integer
there is a unique integer 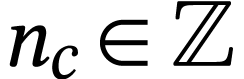 with
with 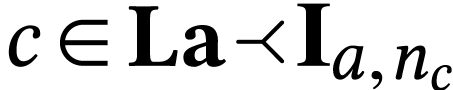 . The equations (5) and (6)
imply that if
. The equations (5) and (6)
imply that if 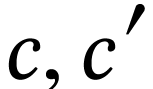 are elements of
are elements of  with
with 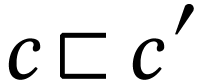 , then we must have
, then we must have
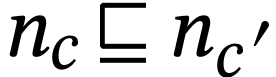 . It follows that
. It follows that 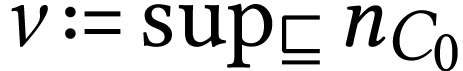 exists in
exists in 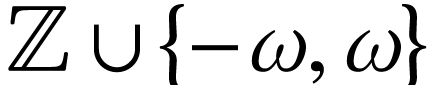 . If
. If
 where
where 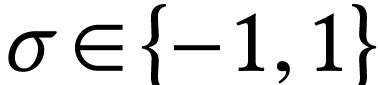 ,
then
,
then 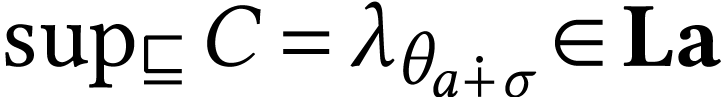 . If
. If 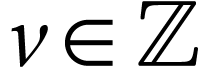 , then for
, then for  with
with 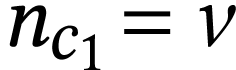 and
and 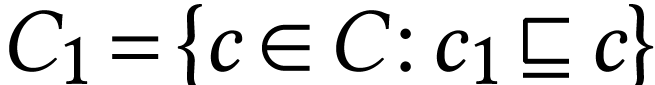 , we
have
, we
have 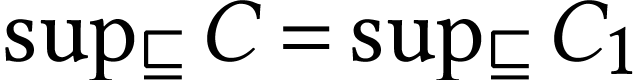 and
and 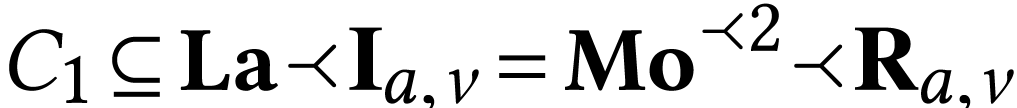 .
The structure
.
The structure 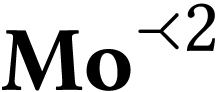 is closed, so by Corollary 30 and Lemma 15, the structure
is closed, so by Corollary 30 and Lemma 15, the structure 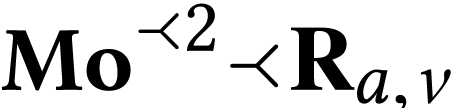 is closed. So
is closed. So  is log-atomic.
is log-atomic.

We apply the results of the previous sections to give the sign sequence
formula for  .
.
 . We have
. We have 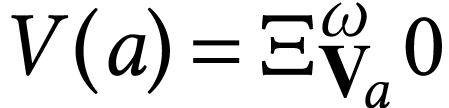 , which is the transfinite concatenation
, which is the transfinite concatenation

As a consequence, we have 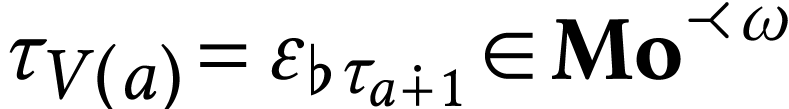 .
.
 is a
direct consequence of the closure of
is a
direct consequence of the closure of 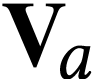 .
The computation of this supremum is left to the reader.
.
The computation of this supremum is left to the reader.

 define
define 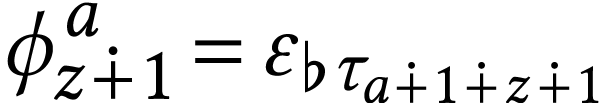 and
and 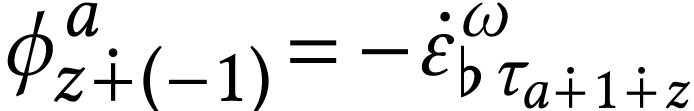 . Let
. Let 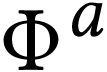 be the function
defined on
be the function
defined on  by
by 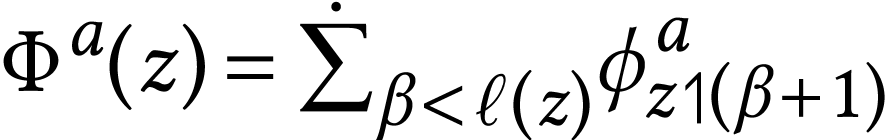 .
We have
.
We have
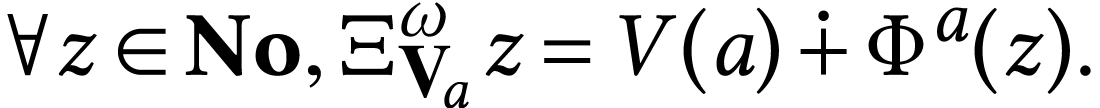
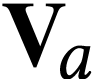 is closed, we
may rely on Proposition 19. We need only prove that for
is closed, we
may rely on Proposition 19. We need only prove that for
 and
and 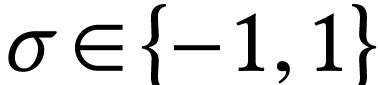 ,
we have
,
we have 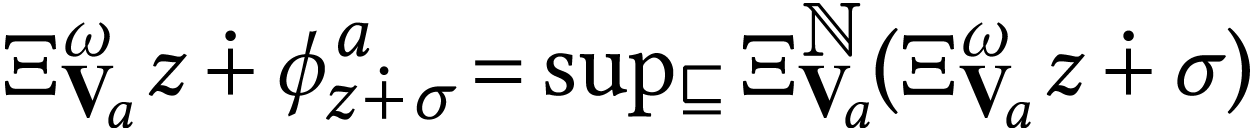 . We prove this by
induction on
. We prove this by
induction on 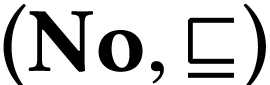 along with the claim that
along with the claim that 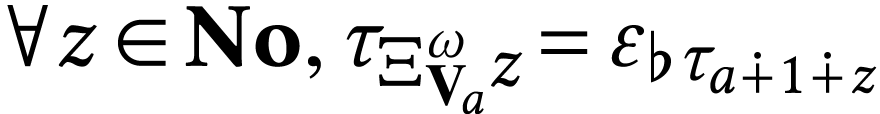 .
.
Note that the functions 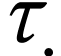 ,
,
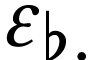 ,
,  and
and
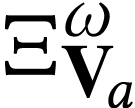 preserve non-empty suprema. Moreover, the
identity
preserve non-empty suprema. Moreover, the
identity 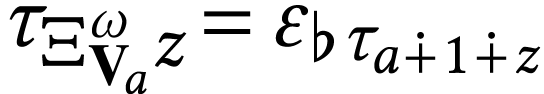 is valid for
is valid for 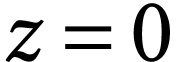 . So by the previous lemma, we need only prove the
claim at successors cases. Let
. So by the previous lemma, we need only prove the
claim at successors cases. Let  ,
set
,
set 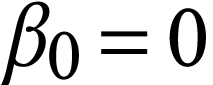 , and define
, and define
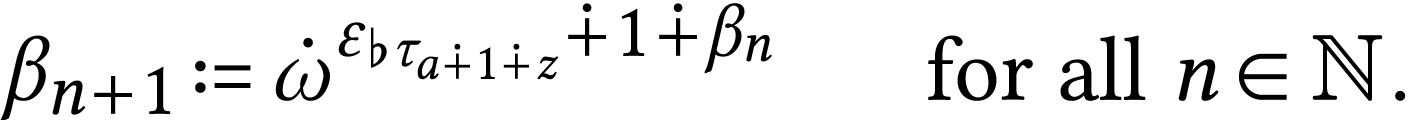
We have 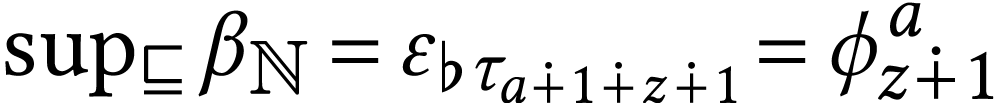 . Let
. Let 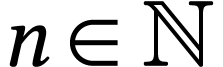 with
with 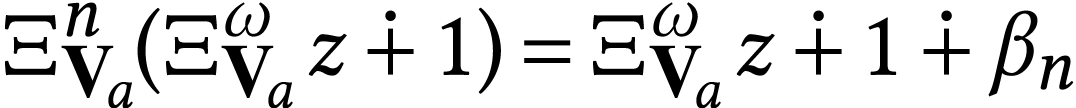 (this is trivially the case
for
(this is trivially the case
for 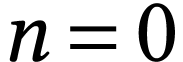 ). We have
). We have
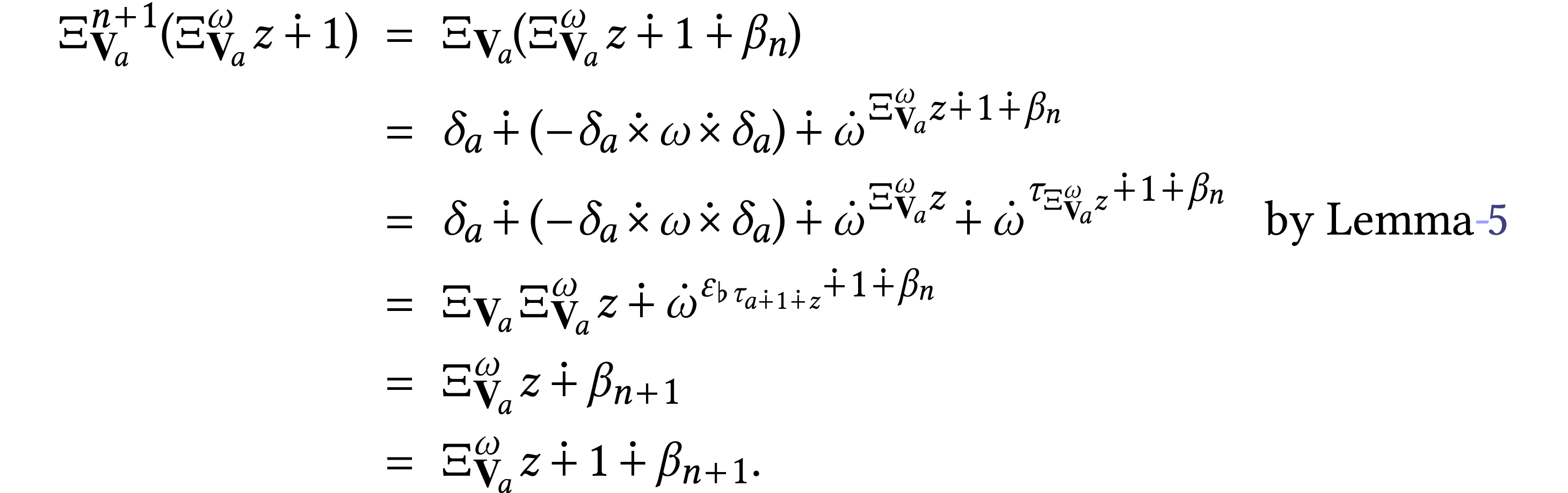
It follows that 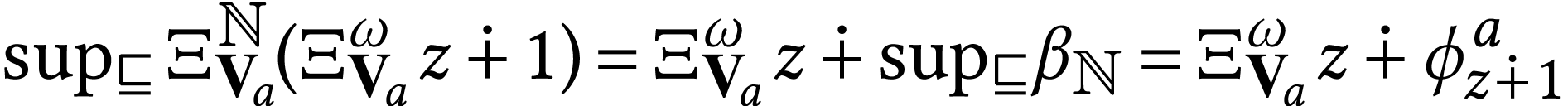 . The second
claim is valid since we have
. The second
claim is valid since we have 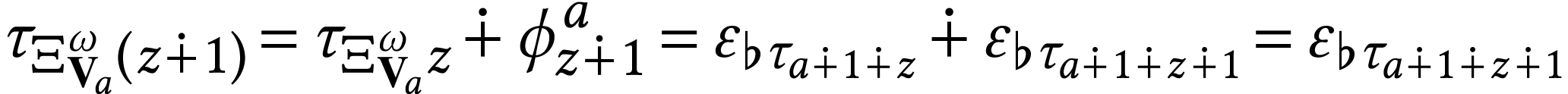 .
Let
.
Let 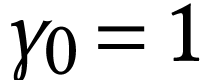 , and for
, and for 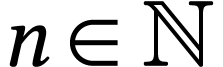 define
define 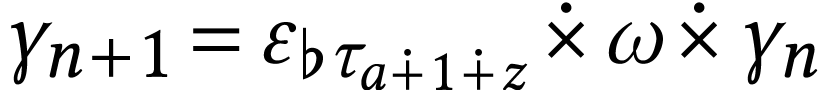 . We
have
. We
have 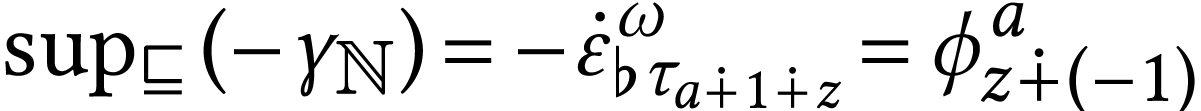 . Let
. Let 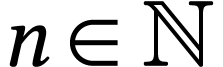 with
with 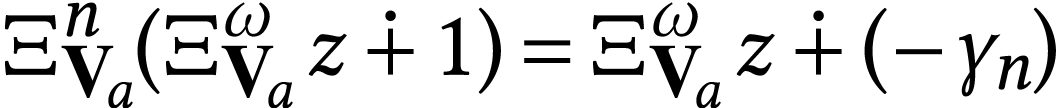 (this is trivially the case for
(this is trivially the case for 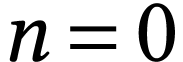 ). We have
). We have
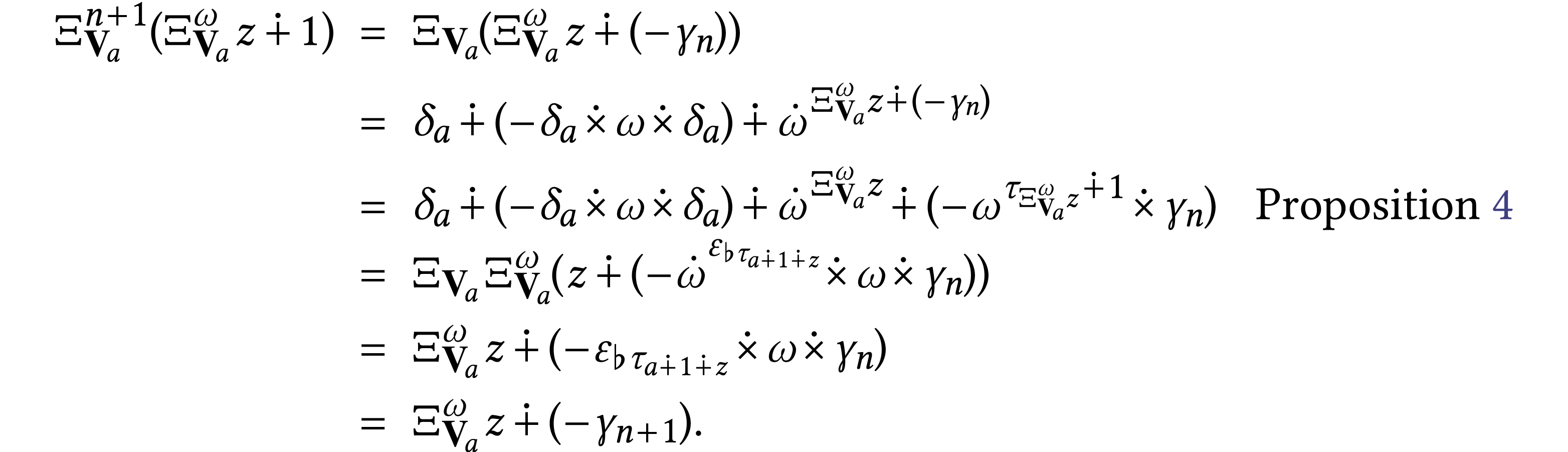
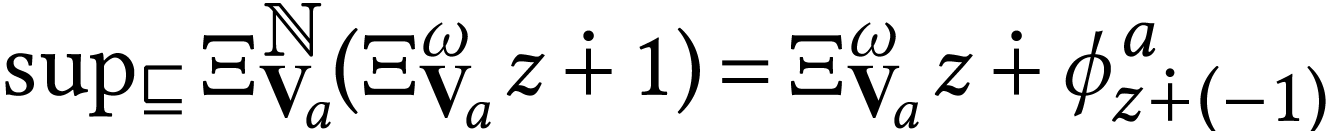 . The second
claim is valid since we have
. The second
claim is valid since we have 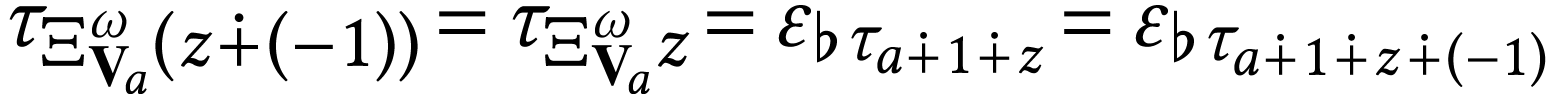 .
This concludes the proof.
.
This concludes the proof.

Our work on sign sequences is summed up in the following table where we
distinguish the cases 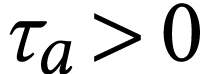 and
and 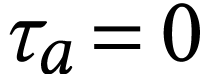 .
.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
In order to obtain the formula for 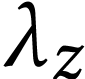 ,
one need only use the relation
,
one need only use the relation 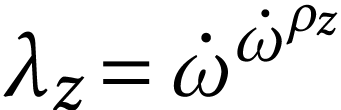 and apply
Proposition 4 twice.
and apply
Proposition 4 twice.
Acknowledgments. This work is supported by the French Belgian Community through a F.R.I.A. grant.
 class of surreal numbers
1
class of surreal numbers
1
 class of ordinal numbers
1
class of ordinal numbers
1
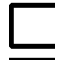 simplicity relation 1
simplicity relation 1
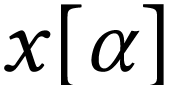
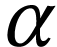 -th
sign of
-th
sign of 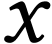 2
2
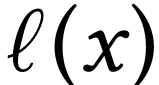 length of
length of 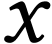 2
2

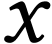 is simpler than
is simpler than 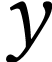 2
2
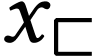 set of strictly simpler numbers
2
set of strictly simpler numbers
2
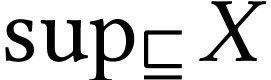 supremum of the chain
supremum of the chain 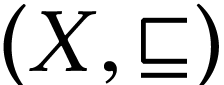 in
in 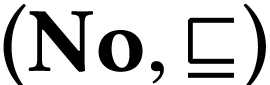 3
3
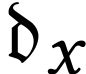 unique monomial in the archimedean class of
unique monomial in the archimedean class of
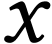 3
3
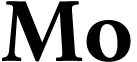 class of monomials 3
class of monomials 3
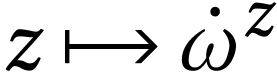
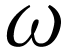 -map,
i.e. parametrization of
-map,
i.e. parametrization of 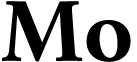 3
3
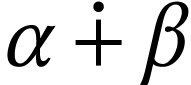 ordinal sum 3
ordinal sum 3
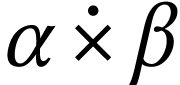 ordinal product 3
ordinal product 3
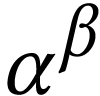 ordinal exponentiation
3
ordinal exponentiation
3
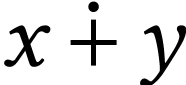 sum concatenation 3
sum concatenation 3
 product concatenation
3
product concatenation
3

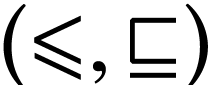 -isomorphism
-isomorphism
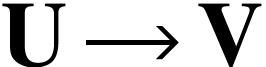 6
6
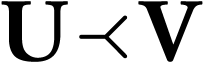 imbrication
imbrication  of
of 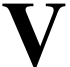 into
into  6
6
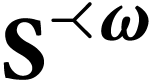 class of fixed points of
class of fixed points of 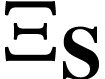 6
6
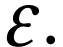 parametrization of
parametrization of 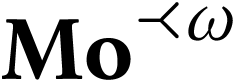 7
7
exp Gonshor's exponential function 9
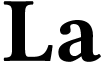 class of log-atomic numbers
9
class of log-atomic numbers
9
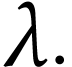 parametrization of
parametrization of 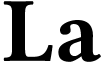 9
9
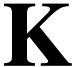 class of
class of  -numbers
10
-numbers
10
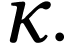 parametrization of
parametrization of 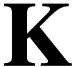 10
10
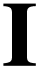 structure with
structure with  11
11
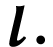 parametrization of
parametrization of 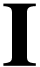 11
11
 structure with
structure with  11
11
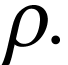 parametrization of
parametrization of  11
11
M. Aschenbrenner, L. van den Dries, and J. van der Hoeven. Asymptotic Differential Algebra and Model Theory of Transseries. Number 195 in Annals of Mathematics studies. Princeton University Press, 2017.
M. Aschenbrenner, L. van den Dries, and J. van der
Hoeven. The surreal numbers as a universal 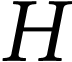 -field. Journal of the European
Mathematical Society, 21(4), 2019.
-field. Journal of the European
Mathematical Society, 21(4), 2019.
V. Bagayoko and J. van der Hoeven. Surreal Substructures. HAL-02151377 (pre-print), 2019.
V. Bagayoko, J. van der Hoeven, and V. Mantova. Defining a surreal hyperexponential. HAL-02861485 (pre-print), 2020.
A. Berarducci and V. Mantova. Surreal numbers, derivations and transseries. JEMS, 20(2):339–390, 2018.
A. Berarducci and V. Mantova. Transseries as germs of surreal functions. Transactions of the American Mathematical Society, 371:3549–3592, 2019.
L. van den Dries and Ph. Ehrlich. Fields of surreal numbers and exponentiation. Fundamenta Mathematicae, 167(2):173–188, 2001.
H. Gonshor. An Introduction to the Theory of Surreal Numbers. Cambridge Univ. Press, 1986.
H. Hahn. Über die nichtarchimedischen Größensysteme. Sitz. Akad. Wiss. Wien, 116:601–655, 1907.
I. Kaplansky. Maximal fields with valuations, ii. Duke Mathematical Journal, 12(2):243–248, 06 1945.
H. Kneser. Reelle analytische lösung der
gleichung 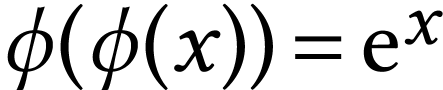 und verwandter
funktionalgleichungen. Journal Für Die Reine Und
Angewandte Mathematik, 1950:56–67, 01 1950.
und verwandter
funktionalgleichungen. Journal Für Die Reine Und
Angewandte Mathematik, 1950:56–67, 01 1950.
S. Kuhlmann and M. Matusinski. The exponential-logarithmic equivalence classes of surreal numbers. Order 32, pages 53–68, 2015.
V. Mantova and M. Matusinski. Surreal numbers with derivation, Hardy fields and transseries: a survey. Contemporary Mathematics, pages 265–290, 2017.