Conway's class |
|
Conway's class |
Let  be Conway's class of surreal numbers [7]. It is well known that
be Conway's class of surreal numbers [7]. It is well known that  has a rich
structure: Conway showed that
has a rich
structure: Conway showed that  forms a real
closed field and Gonshor also defined an exponential function
forms a real
closed field and Gonshor also defined an exponential function 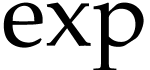 on
on  that satisfies the same first
order theory as the usual exponential function on the reals [11,
8]. Following Conway's tradition, all numbers will
be understood to be surreal in what follows.
that satisfies the same first
order theory as the usual exponential function on the reals [11,
8]. Following Conway's tradition, all numbers will
be understood to be surreal in what follows.
Let 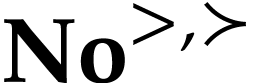 be the class of positive infinitely large
numbers, i.e. numbers that are larger than any integer. The
aim of this note is to define an increasing and bijective function
be the class of positive infinitely large
numbers, i.e. numbers that are larger than any integer. The
aim of this note is to define an increasing and bijective function 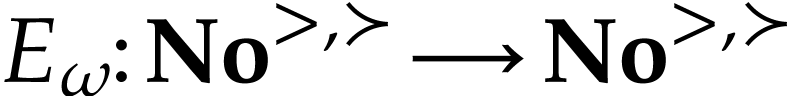 that satisfies the functional equation
that satisfies the functional equation
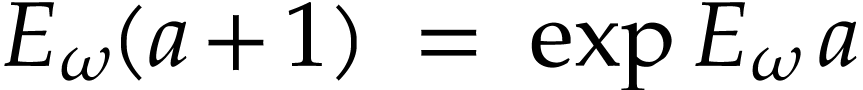 |
(1) |
for all  . Since this equation
has many solutions, one difficulty is to single out a particular
solution. Now one interesting property for surreal functions is
surreal-analyticity [5], i.e. the
existence of Taylor expansions around every point. In our final section,
we prove that our function
. Since this equation
has many solutions, one difficulty is to single out a particular
solution. Now one interesting property for surreal functions is
surreal-analyticity [5], i.e. the
existence of Taylor expansions around every point. In our final section,
we prove that our function  is the simplest
surreal-analytic solution to (1) in a sense that will be
made precise in Definition 21.
is the simplest
surreal-analytic solution to (1) in a sense that will be
made precise in Definition 21.
The function  is called a
hyperexponential and it is the first non-trivial
hyperexponential in the transfinite sequence
is called a
hyperexponential and it is the first non-trivial
hyperexponential in the transfinite sequence 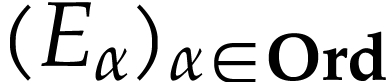 of
iterated exponentials
of
iterated exponentials
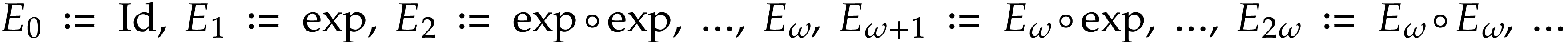
The corresponding functional inverses are called hyperlogarithms:
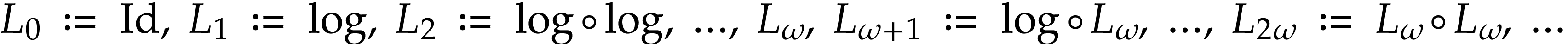
We require such more general hyperexponentials to satisfy 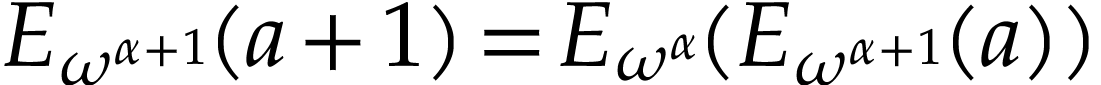 for all ordinals
for all ordinals 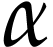 and
and  . Similarly,
. Similarly, 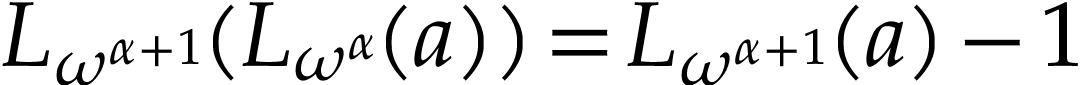 .
.
There are known real analytic solutions of (1) with good
properties [15, 6], even though there does not
seem to exist any meaningful “most natural” solution. It is
also well known that fractional iterates of 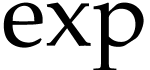 and
and
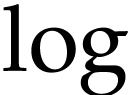 can be defined in terms of
can be defined in terms of  and
and 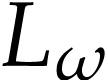 : given
: given 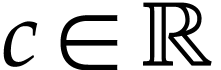 , we take
, we take 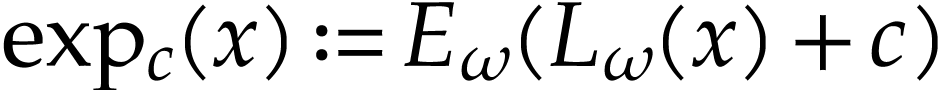 and
and 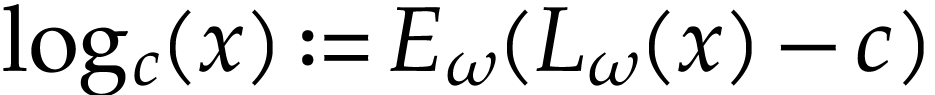 .
.
From a formal perspective, hyperexponentials and hyperseries were
studied in detail by Schmeling and van der Hoeven [18]:
they generalize transseries to include formal counterparts of 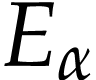 ,
, 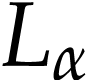 for
for 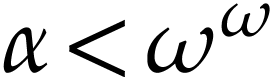 [18]. This yields in particular a
natural hyperexponential on the set of positive infinitely large
transseries. More recently, van den Dries, van der Hoeven and Kaplan [9] constructed the field of logarithmic hyperseries
[18]. This yields in particular a
natural hyperexponential on the set of positive infinitely large
transseries. More recently, van den Dries, van der Hoeven and Kaplan [9] constructed the field of logarithmic hyperseries
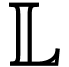 with hyperlogarithms
with hyperlogarithms 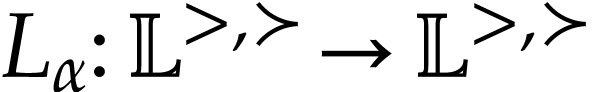 for
all
for
all 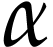 . The ultimate goal [14, 2] is to construct a field of hyperseries
. The ultimate goal [14, 2] is to construct a field of hyperseries
 that is also closed under all hyperexponentials,
together with an isomorphism
that is also closed under all hyperexponentials,
together with an isomorphism 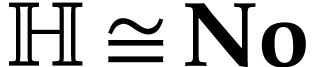 that corresponds to
evaluation of hyperseries at
that corresponds to
evaluation of hyperseries at  .
This work can be considered as another step in this direction, by
constructing the first surreal-valued hyperexponential function
.
This work can be considered as another step in this direction, by
constructing the first surreal-valued hyperexponential function 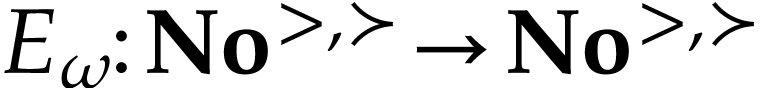 . The higher hyperexponentials
. The higher hyperexponentials 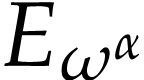 with
with 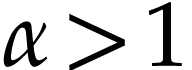 can be constructed in a
similar way, but this more technical generalization will be the subject
of a forthcoming paper.
can be constructed in a
similar way, but this more technical generalization will be the subject
of a forthcoming paper.
The remainder of this introduction starts with some quick reminders about surreal numbers, transseries, and surreal substructures. We next outline the main ideas of our construction, while highlighting a few similarities with the construction of the usual exponential function.
 can be
written as infinite series
can be
written as infinite series
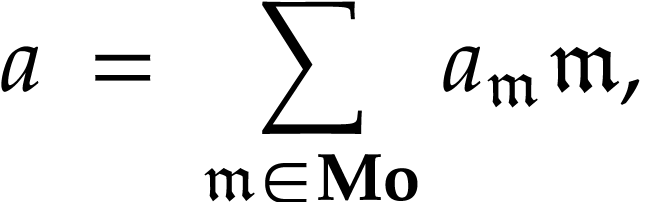
where  denotes the class of surreal
monomials and the coefficients
denotes the class of surreal
monomials and the coefficients 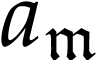 are
real. In particular,
are
real. In particular,  is isomorphic to the Hahn
field
is isomorphic to the Hahn
field 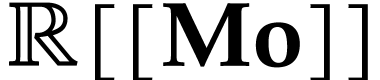 of formal power series. Together with the
exponential function,
of formal power series. Together with the
exponential function,  even admits the structure
of a field of transseries in the sense of [18];
see [4]. Our definition of
even admits the structure
of a field of transseries in the sense of [18];
see [4]. Our definition of  will
rely on this existing structure on
will
rely on this existing structure on  ,
and in particular on the fact that certain transseries act as functions
on surreal numbers [5].
,
and in particular on the fact that certain transseries act as functions
on surreal numbers [5].
We will freely use notations from [1, 14] when
dealing with such transseries. In particular given  , we define
, we define
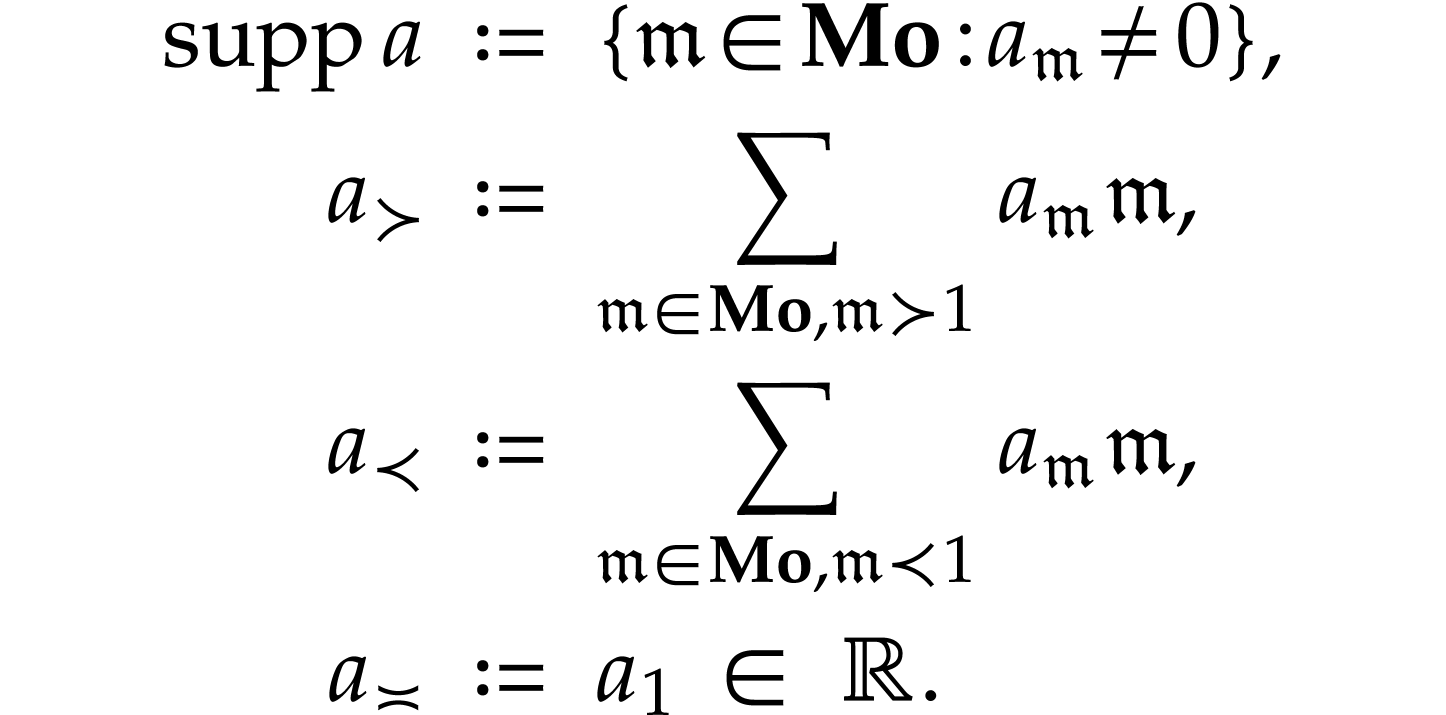
The set 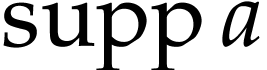 is called the support of
is called the support of 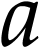 ; it is always a set (as opposed to
a proper class) and it is reverse well ordered. For
; it is always a set (as opposed to
a proper class) and it is reverse well ordered. For  we set
we set
When  , we say that
, we say that  is a truncation of
is a truncation of 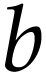 .
We also define
.
We also define
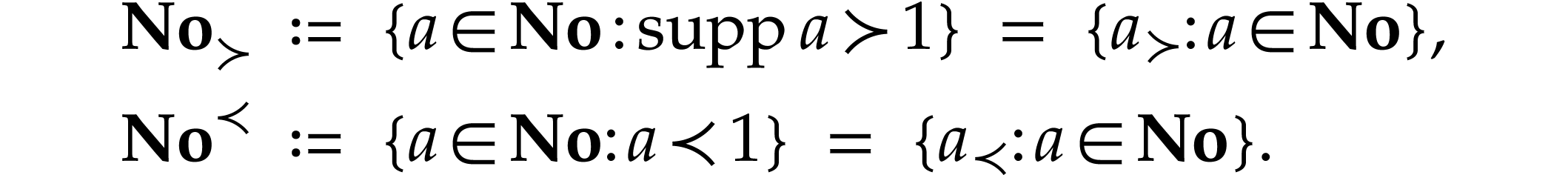
 and decompose it as
and decompose it as 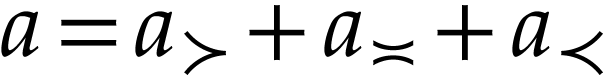 with
with  ,
,
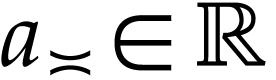 , and
, and  . Then the functional equation of
. Then the functional equation of 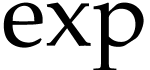 yields
yields
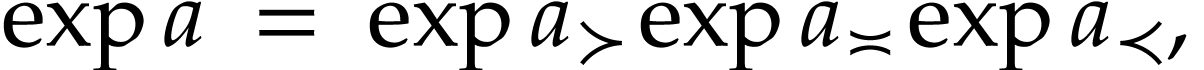 |
(2) |
where 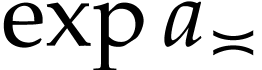 is the usual exponential in
is the usual exponential in  and
and 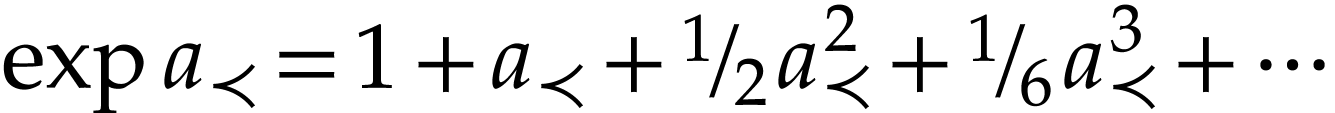 . In order
to define
. In order
to define 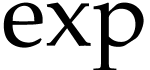 on
on  ,
this relation shows that it would have sufficed to define it on
,
this relation shows that it would have sufficed to define it on 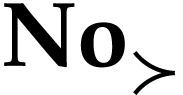 . In addition, it can be shown that
. In addition, it can be shown that
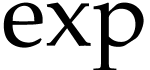 bijectively maps the class
bijectively maps the class 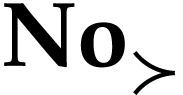 to the class
to the class  . Our process to
define
. Our process to
define  is similar, with different subclasses
is similar, with different subclasses
 and
and 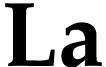 in the roles of
in the roles of 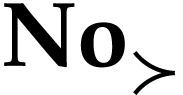 and
and  . The
class
. The
class  is defined below and
is defined below and 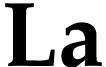 is the class of log-atomic numbers, i.e. numbers
is the class of log-atomic numbers, i.e. numbers
 such that
such that 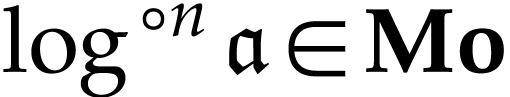 for all
for all  .
.
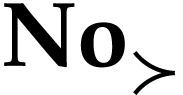 ,
,
 ,
,  , and
, and 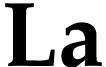 are examples of
so-called surreal substructures, which were extensively studied in [3]. Let us quickly recall a few basic facts about surreal
substructures; see also section 2.
are examples of
so-called surreal substructures, which were extensively studied in [3]. Let us quickly recall a few basic facts about surreal
substructures; see also section 2.
Besides the usual ordering, the class  of surreal
numbers comes with a well-founded partial order
of surreal
numbers comes with a well-founded partial order  called the simplicity relation. A surreal substructure
is a subclass
called the simplicity relation. A surreal substructure
is a subclass 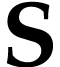 of
of  that is
isomorphic to
that is
isomorphic to  for the induced relations by
for the induced relations by 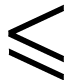 and
and  on
on 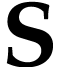 . Equivalently, this means that for any subsets
. Equivalently, this means that for any subsets 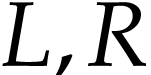 of
of 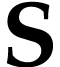 with
with 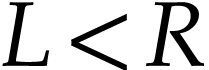 , the cut
, the cut
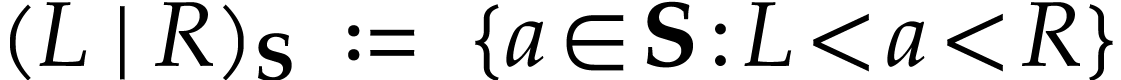
in 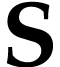 admits a
admits a  -minimum
which is then denoted by
-minimum
which is then denoted by 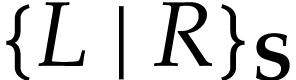 . We
call
. We
call  a cut representation in
a cut representation in 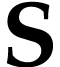 . We extend this notation to the
case when
. We extend this notation to the
case when 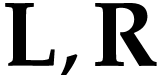 are classes, provided
are classes, provided 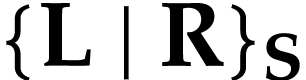 indeed exists. If
indeed exists. If 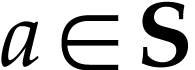 , then we
let
, then we
let
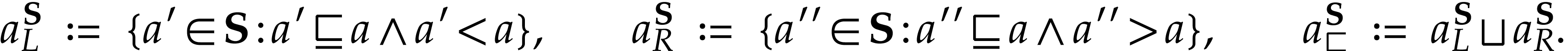
Then 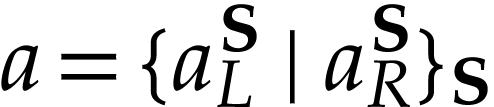 . Moreover, for any cut
. Moreover, for any cut
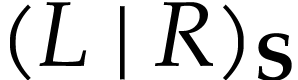 in
in 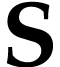 containing
containing 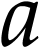 such that
such that 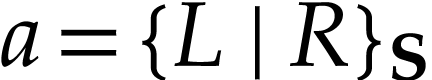 , the
set
, the
set 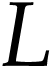 (resp.
(resp. 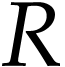 ) is cofinal (resp. coinitial) with
respect to
) is cofinal (resp. coinitial) with
respect to 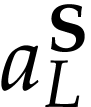 (resp.
(resp. 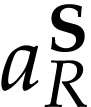 ).
).
Surreal substructures are particularly well-suited for defining
functions via well-founded induction on  , as will be the case for certain restrictions of
, as will be the case for certain restrictions of
 . Important examples of
surreal substructures include
. Important examples of
surreal substructures include  ,
the class
,
the class  of strictly positive numbers, the
class
of strictly positive numbers, the
class 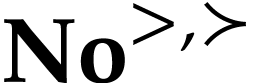 of positive infinitely large numbers, the
classes
of positive infinitely large numbers, the
classes  and
and  of monomials
and infinite monomials, the class
of monomials
and infinite monomials, the class 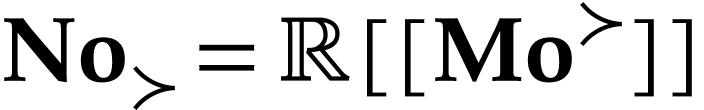 of purely
infinite numbers, and the class
of purely
infinite numbers, and the class 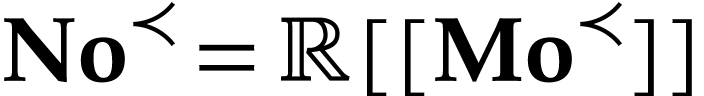 of infinitesimal
numbers.
of infinitesimal
numbers.
 in the
construction of
in the
construction of  ; more
details will be provided in section 4. Assume that
; more
details will be provided in section 4. Assume that  has been defined for some positive purely infinite
number
has been defined for some positive purely infinite
number 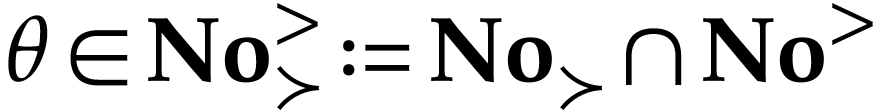 . For sufficiently
small
. For sufficiently
small  , we wish to define
, we wish to define
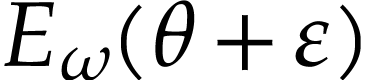 using the Taylor series expansion:
using the Taylor series expansion:
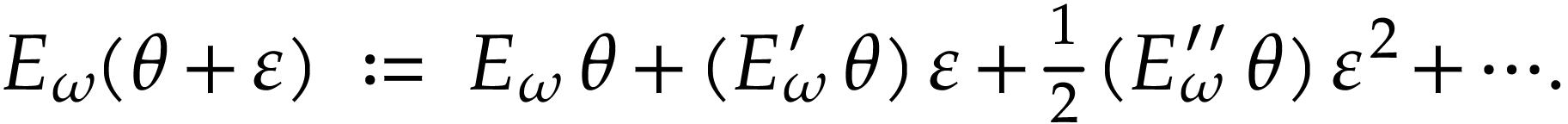 |
(3) |
The successive derivatives 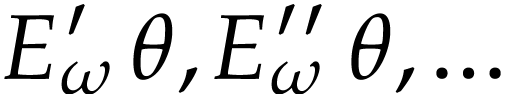 can be defined in
can be defined in
 as ordinary (and so-called logarithmic)
transseries applied to
as ordinary (and so-called logarithmic)
transseries applied to 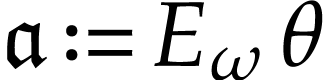 :
:
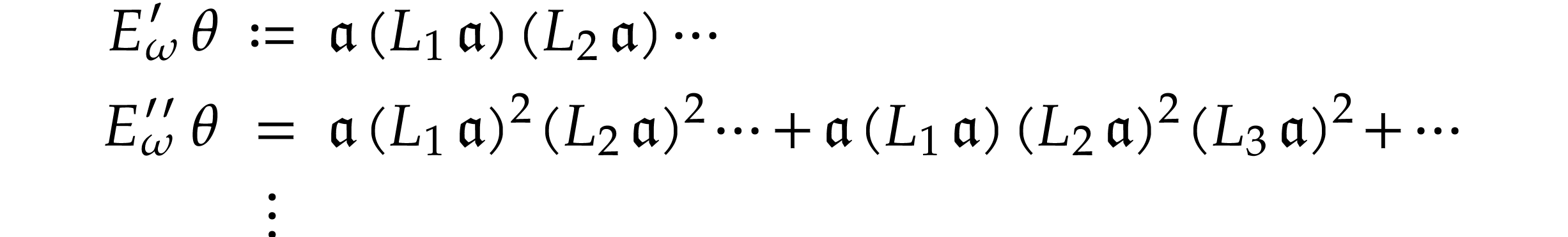
It can be shown that (3) converges formally, provided that
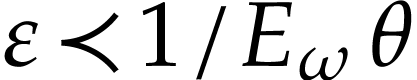 (see Lemma 4 below). More
generally, consider
(see Lemma 4 below). More
generally, consider  with
with 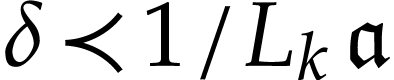 for a certain
for a certain 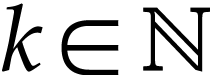 . Assuming (1), this means that
. Assuming (1), this means that 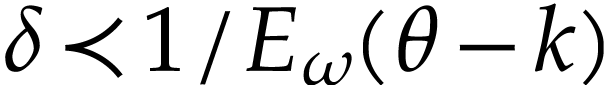 .
We will see that this inequality allows us to define
.
We will see that this inequality allows us to define
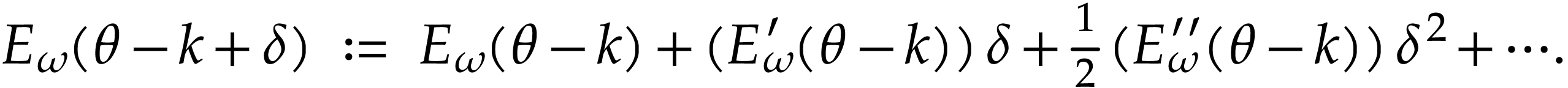 |
(4) |
In view of (1), one must then set
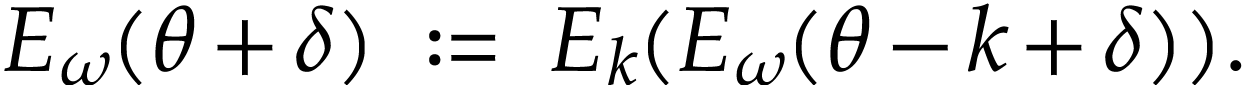 |
(5) |
It will thus be sufficient (see the discussion after Corollary 8)
to define  at all numbers
at all numbers  with
with
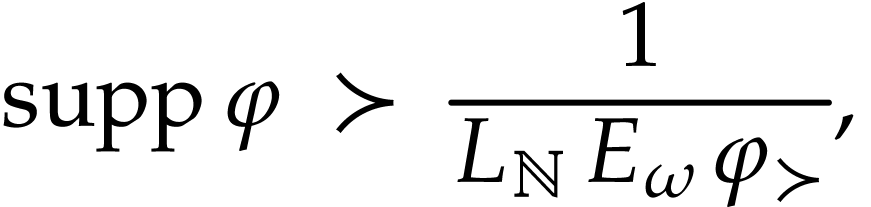
where 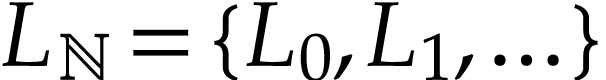 , and then extend
, and then extend  at
at 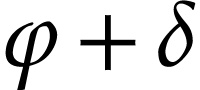 for
for 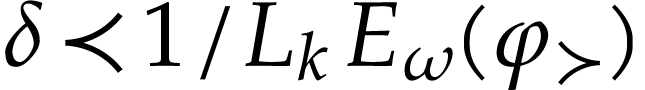 as in (4) and (5). Those numbers
as in (4) and (5). Those numbers  are said to be truncated and we will write
are said to be truncated and we will write  for the class of all truncated numbers. It turns out
that
for the class of all truncated numbers. It turns out
that  is a surreal substructure.
is a surreal substructure.
 proceeds in three stages:
proceeds in three stages:
We first define  on
on  . For any two positive purely infinite
numbers
. For any two positive purely infinite
numbers 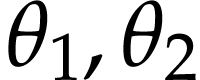 with
with 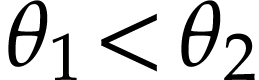 ,
we have
,
we have 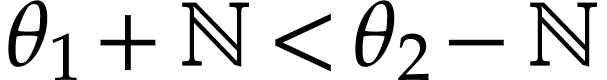 . By the
functional equation, we should have
. By the
functional equation, we should have 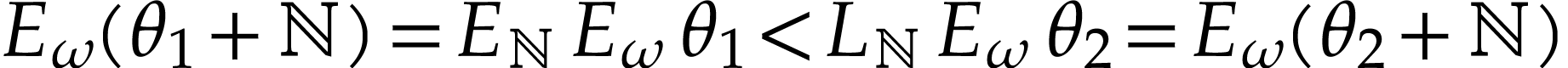 .
We deduce that for
.
We deduce that for  , the
number
, the
number 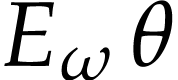 should lie in the cut
should lie in the cut 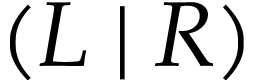 in
in  where
where
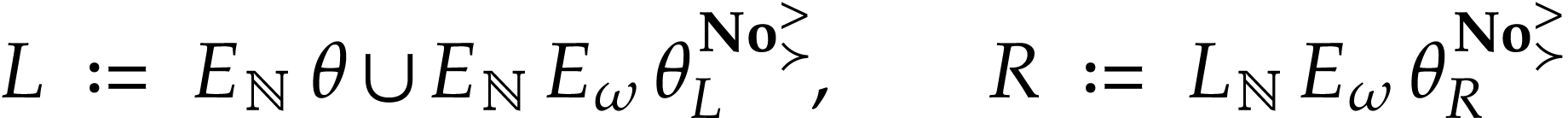
The simplest way to ensure this is to define
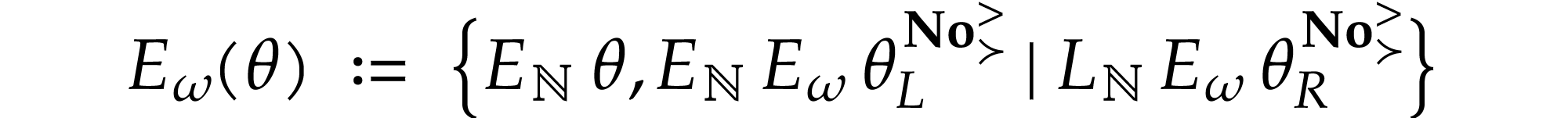
for all  .
.
We next extend  to
to  . Similar arguments and the simplicity
heuristic impose
. Similar arguments and the simplicity
heuristic impose
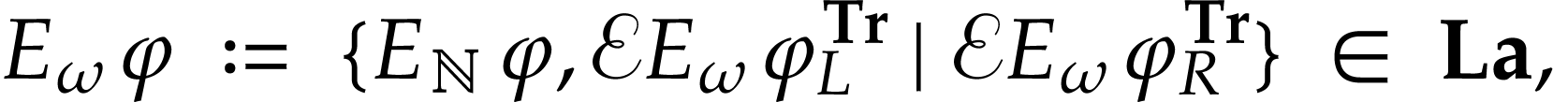
where 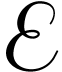 is a function group to be defined in
Section 2. Here
is a function group to be defined in
Section 2. Here  ,
,
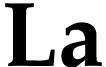 , and (3)
play a similar role as
, and (3)
play a similar role as 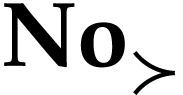 ,
,
 , and (2)
for the definition of
, and (2)
for the definition of 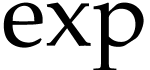 .
.
We finally extend the definition of  to
to 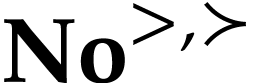 by relying on (4) and (5).
by relying on (4) and (5).
Before we define  , let us
briefly recall a general method from [3, Section 6] to
define surreal substructures using convex partitions and function
groups. In section 4, we will use this to show that
, let us
briefly recall a general method from [3, Section 6] to
define surreal substructures using convex partitions and function
groups. In section 4, we will use this to show that 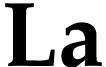 and
and  are indeed surreal
substructures.
are indeed surreal
substructures.
 be a surreal substructure and
be a surreal substructure and 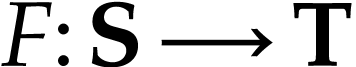 be a function. Let
be a function. Let 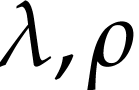 be functions
defined for cut representations in
be functions
defined for cut representations in  and such
that
and such
that 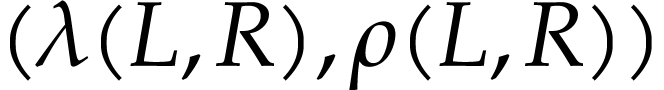 is a cut representation in
is a cut representation in  whenever
whenever 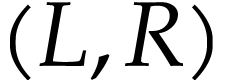 is a cut representation
in
is a cut representation
in 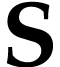 . We say that
. We say that 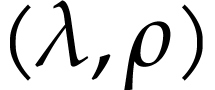 is a cut equation of
is a cut equation of 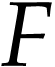 if, for all
if, for all 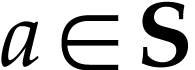 , we have
, we have
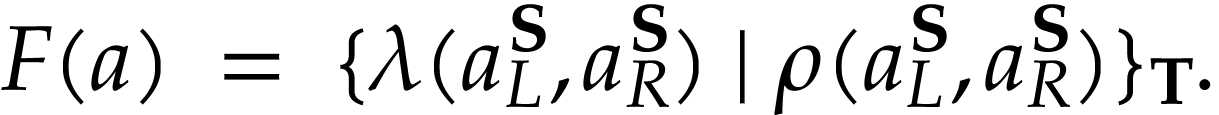
We say that the cut equation is uniform if we have
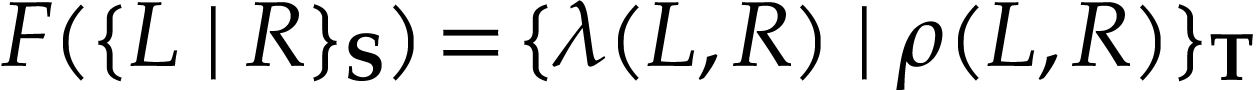 whenever
whenever 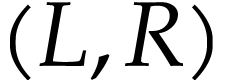 is a cut
representation in
is a cut
representation in 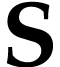 . For
instance, by [11, Theorem 3.2], for
. For
instance, by [11, Theorem 3.2], for 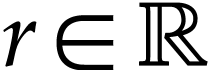 , the following cut equation for the translation
, the following cut equation for the translation
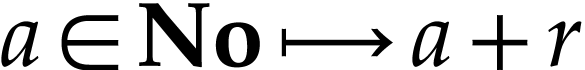 by
by 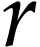 is uniform:
is uniform:
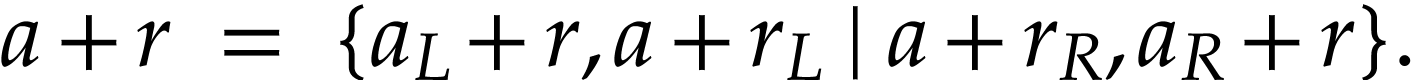 |
(6) |
Remark 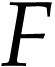 has a cut equation
has a cut equation 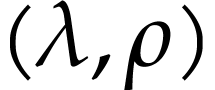 such that for all
such that for all 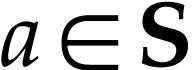 , we have
, we have
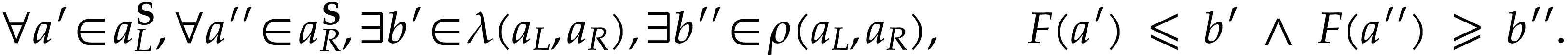
This is trivially the case for 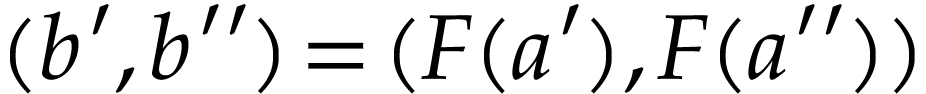 if
if 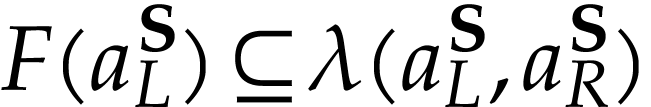 and
and 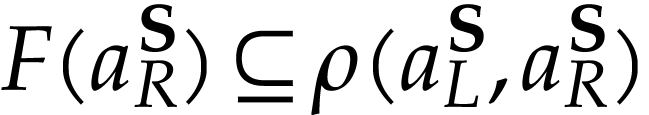 for all
for all  . Then we claim that
. Then we claim that 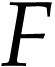 is
strictly increasing. To see this, consider
is
strictly increasing. To see this, consider 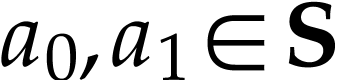 with
with
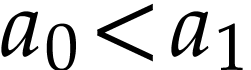 . By [3,
Proposition 4.6], there is a
. By [3,
Proposition 4.6], there is a  -maximal
element
-maximal
element 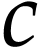 of
of 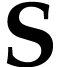 with
with 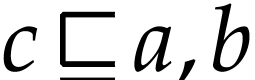 , and we have
, and we have 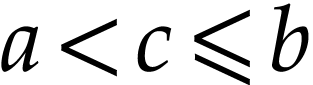 or
or 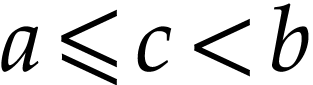 . We treat the first case,
the other one being symmetric. Since
. We treat the first case,
the other one being symmetric. Since 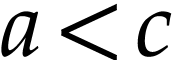 and
and  , we have
, we have 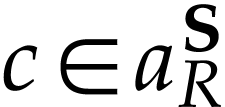 so there is
so there is 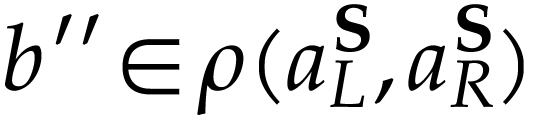 with
with 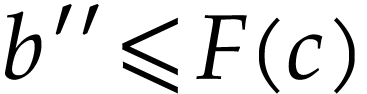 .
We have
.
We have 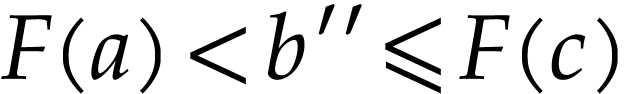 . A similar argument
yields
. A similar argument
yields 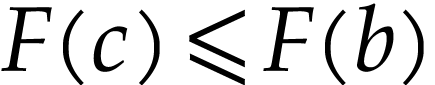 , so
, so 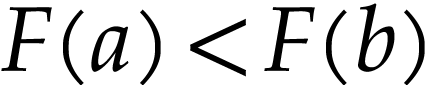 .
.
Note that the existence of 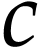 relies on the fact
that
relies on the fact
that 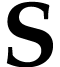 is a surreal substructure. We will use this
result in order to deduce that our definitions of
is a surreal substructure. We will use this
result in order to deduce that our definitions of  on
on 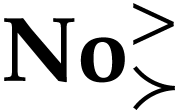 and
and  yield strictly
increasing functions.
yield strictly
increasing functions.
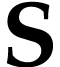 be a surreal substructure and let
be a surreal substructure and let  be a partition of
be a partition of 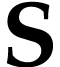 into
convex subclasses, each of which admits a cofinal and coinitial
subset. We refer to
into
convex subclasses, each of which admits a cofinal and coinitial
subset. We refer to  as a thin convex
partition of
as a thin convex
partition of 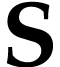 . For
. For
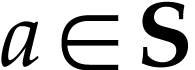 , we let
, we let 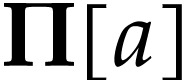 denote the unique member of
denote the unique member of  containing
containing 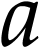 . We also write
. We also write 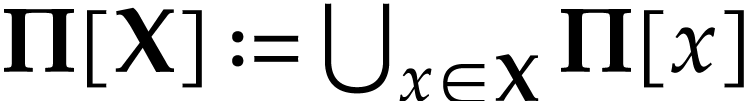 for any subclass
for any subclass  of
of 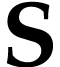 . We say that an element
. We say that an element 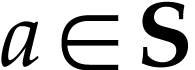 is
is  -simple if it
is the
-simple if it
is the  -minimum of its
class
-minimum of its
class 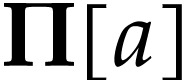 . This is equivalent
to the existence of a cut
. This is equivalent
to the existence of a cut 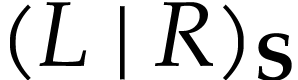 in
in  with
with 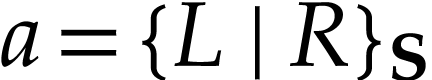 and
and 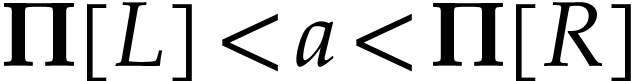 .
.
Then the class 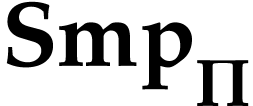 of
of  -simple
elements forms a surreal substructure which is contained in
-simple
elements forms a surreal substructure which is contained in 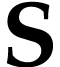 [3, Theorem 6.7]. For
[3, Theorem 6.7]. For 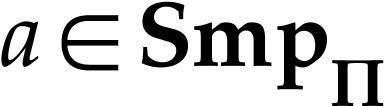 , we have
, we have 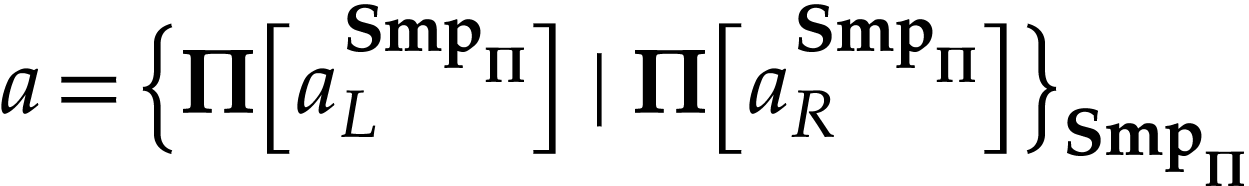 [3,
Proposition 6.8].
[3,
Proposition 6.8].
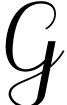 on a surreal
substructure
on a surreal
substructure 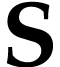 is a group of strictly increasing
bijections
is a group of strictly increasing
bijections  under functional composition. We
regard elements
under functional composition. We
regard elements 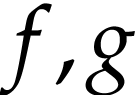 of
of 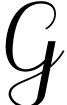 as
actions on
as
actions on 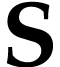 and sometimes write
and sometimes write  and
and 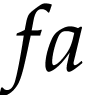 for
for 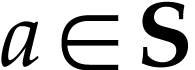 rather than
rather than 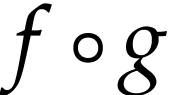 and
and 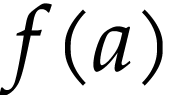 .
For such a function group
.
For such a function group 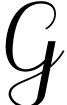 ,
the collection
,
the collection 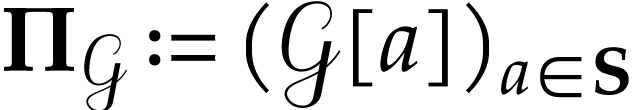 of classes
of classes
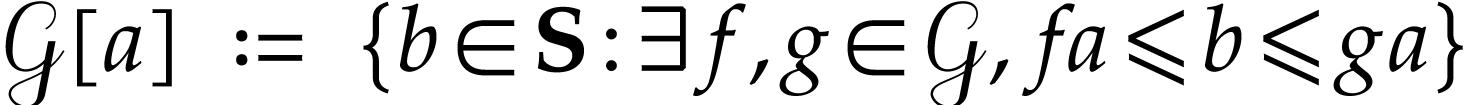
is a thin convex partition of 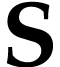 [3,
Proposition 6.25] and we define
[3,
Proposition 6.25] and we define 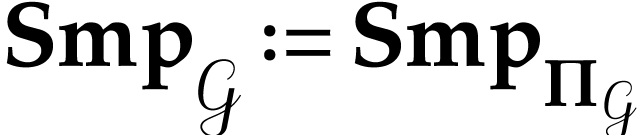 .
.
For 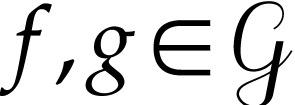 , the relation
, the relation 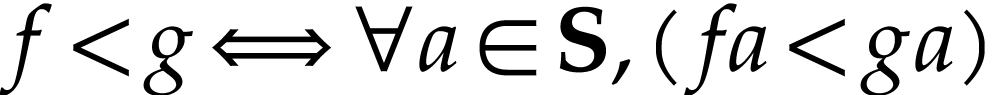 is a partial order on
is a partial order on 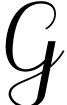 .
We will frequently rely on the elementary fact that
.
We will frequently rely on the elementary fact that 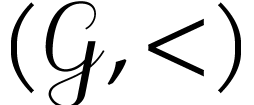 is partially bi-ordered, i.e. that we have
is partially bi-ordered, i.e. that we have
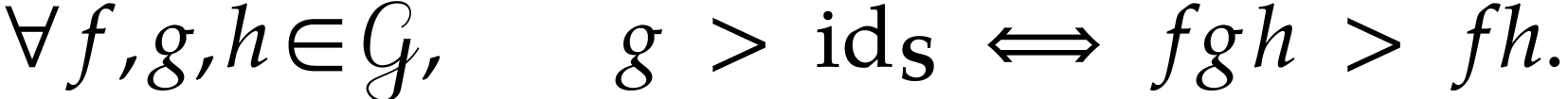
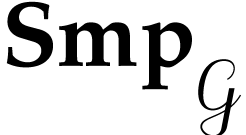 for actions of the following function groups
for actions of the following function groups
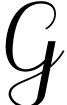 acting on
acting on  ,
,
 or
or 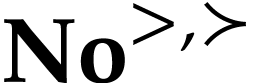 .
For
.
For 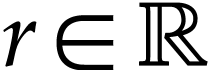 and
and 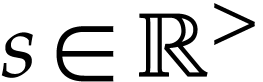 ,
we define
,
we define
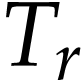 |
 |
 |
acting on  or or 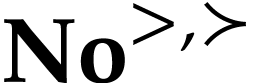 |
 |
 |
 |
acting on  or or 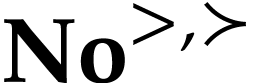 |
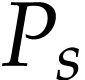 |
 |
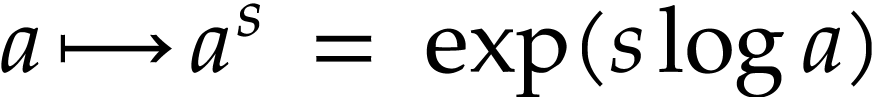 |
acting on  or or 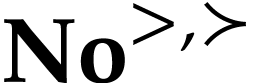 |
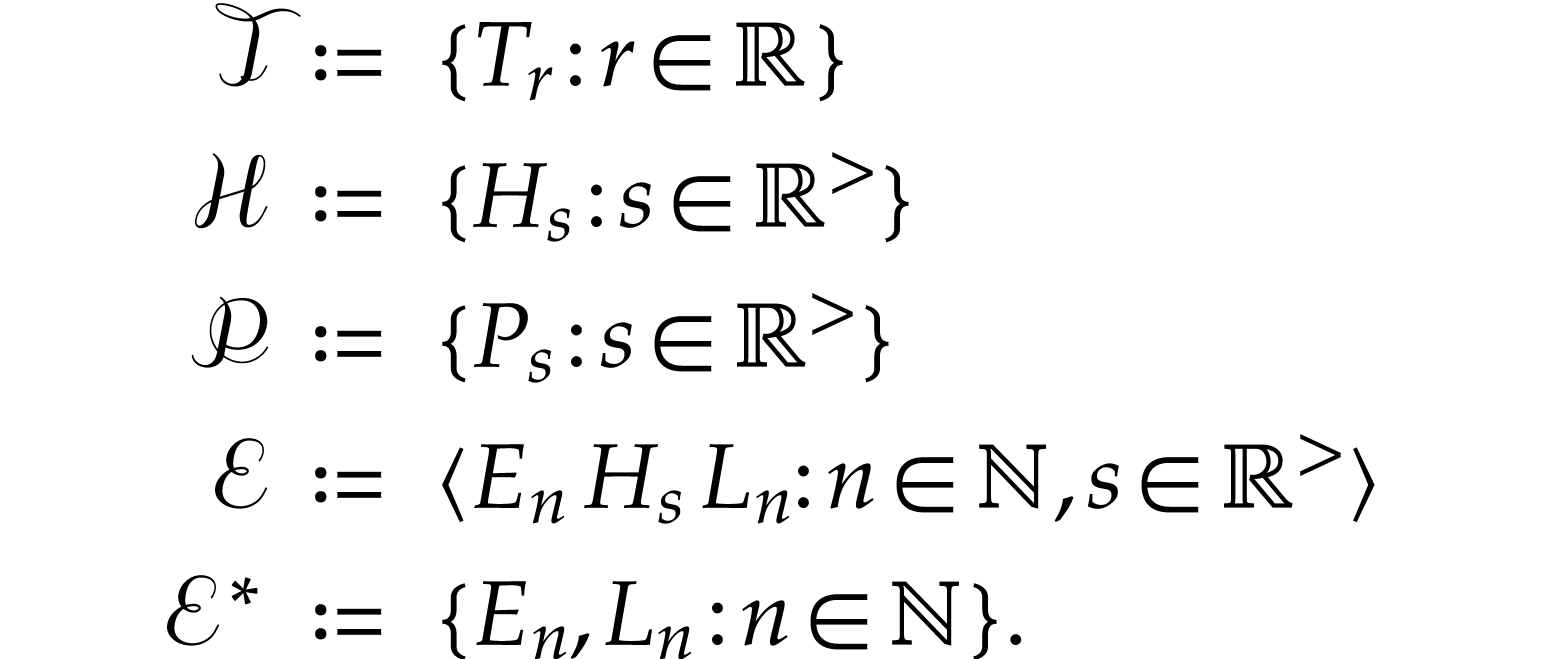
We then have the following list of identities [3, Section 7.1]:
The action of  on
on  (resp.
(resp. 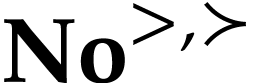 ) yields
) yields 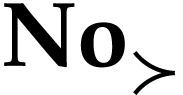 (resp.
(resp. 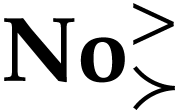 ).
).
The action of  on
on  (resp.
(resp. 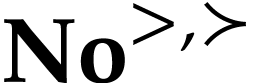 ) yields
) yields  (resp.
(resp.  ).
).
The action of  on
on 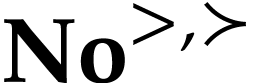 yields
yields 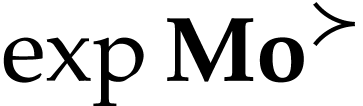 .
.
The action of 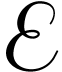 on
on 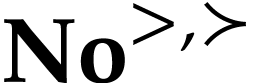 yields
yields 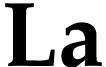 [4, Corollary 5.17].
[4, Corollary 5.17].
The action of  on
on 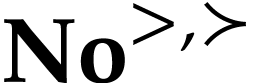 yields the class
yields the class 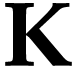 of [16].
of [16].
The groups 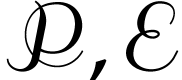 ,
, will play an important role in this paper. Here we note the analogy
between the roles of
will play an important role in this paper. Here we note the analogy
between the roles of  with respect to
with respect to  and
and 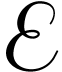 with respect to
with respect to 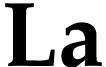 . The above function groups and identities also
turn out to be convenient for asymptotic growth computations that
involve
. The above function groups and identities also
turn out to be convenient for asymptotic growth computations that
involve 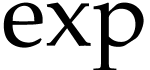 ,
, 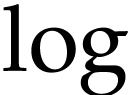 ,
,  ,
and
,
and 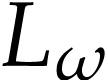 . For
. For  , we define
, we define 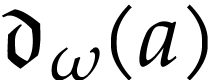 to be the
unique log-atomic element of
to be the
unique log-atomic element of 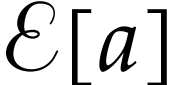 and
and 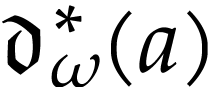 to be the unique element of
to be the unique element of 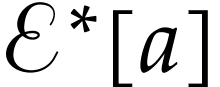 inside
inside
 . We have
. We have 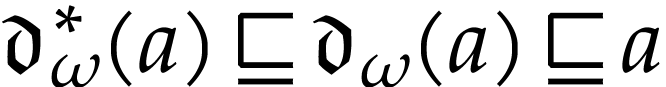 , by definition.
, by definition.
Let us briefly recall some basic definitions and facts about logarithmic
hyperseries from [9]. Given an ordinal 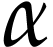 , let
, let  be the set of
formal power products
be the set of
formal power products  , for
some function
, for
some function 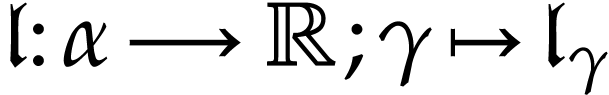 . This set
carries a natural group structure and we define the monomial ordering
. This set
carries a natural group structure and we define the monomial ordering
 on
on 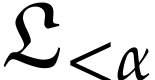 by setting
by setting  if and only if
if and only if 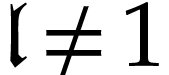 and
and 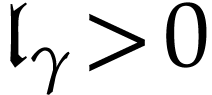 for
for 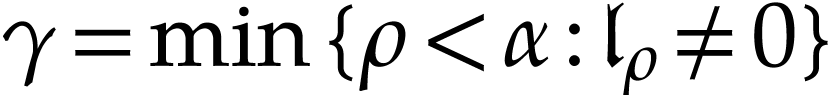 . We call
. We call
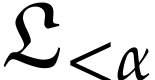 the monomial group of logarithmic
hypermonomials of force
the monomial group of logarithmic
hypermonomials of force 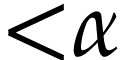 .
.
Since 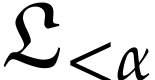 is a monomial group, we may form the Hahn
field
is a monomial group, we may form the Hahn
field 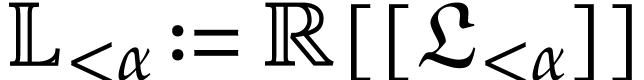 and call it the field of logarithmic
hyperseries of force
and call it the field of logarithmic
hyperseries of force  .
The elements of
.
The elements of 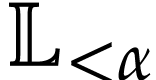 are formal sums
are formal sums 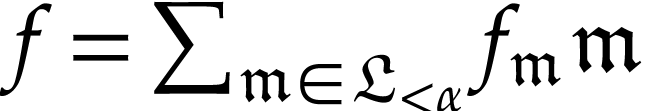 for which the support
for which the support 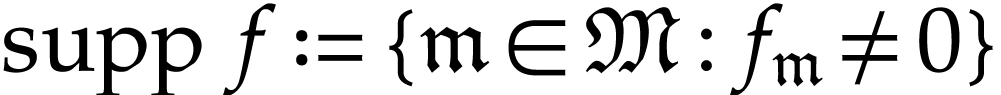 contains no infinite
strictly increasing sequences for
contains no infinite
strictly increasing sequences for  (we say that
(we say that
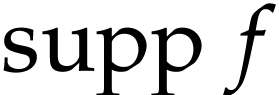 is well-based). In particular, the
support of any non-zero series
is well-based). In particular, the
support of any non-zero series 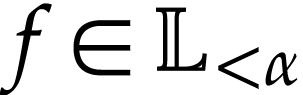 has a maximal
element
has a maximal
element 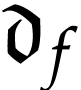 that we call the dominant
monomial of
that we call the dominant
monomial of 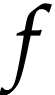 . We also
declare
. We also
declare 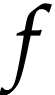 to be positive if
to be positive if 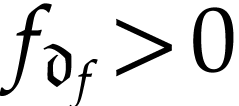 and this gives
and this gives  the structure of a real closed
field.
the structure of a real closed
field.
The ordered field  is also equipped with a
derivation whose values at monomials
is also equipped with a
derivation whose values at monomials  are given
by
are given
by
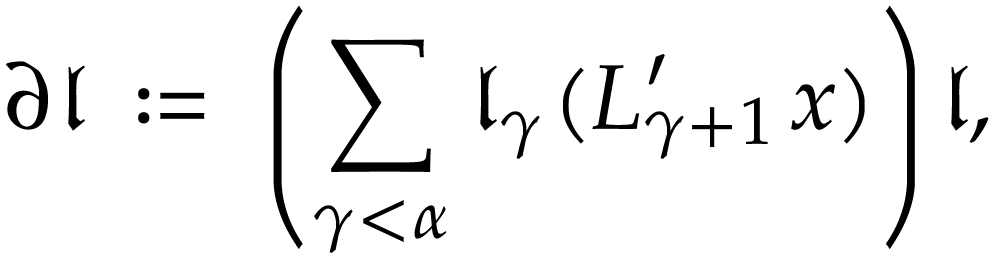
where 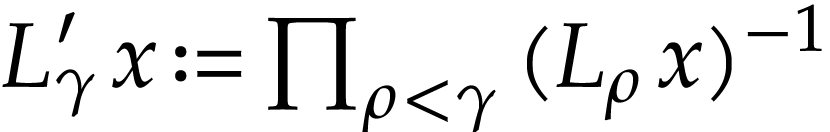 for all
for all 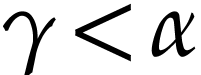 .
This derivation is strongly linear in the sense that it
preserves infinite sums, whenever defined.
.
This derivation is strongly linear in the sense that it
preserves infinite sums, whenever defined.
In [13], the theory of Hahn fields was generalized to
partially ordered monomial monoids and series with Noetherian support
(no infinite increasing sequences and no infinite antichains). Recall
from there that 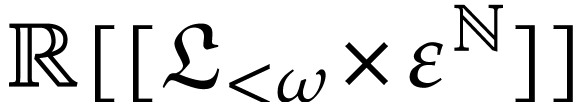 stands for the set of series
with Noetherian support in the partially ordered set
stands for the set of series
with Noetherian support in the partially ordered set 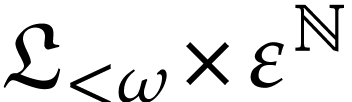 . We may consider elements of
. We may consider elements of 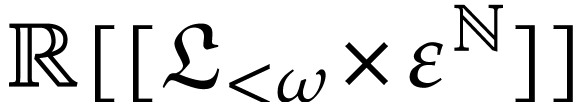 as bivariate series that are logarithmic transseries with respect to
as bivariate series that are logarithmic transseries with respect to
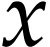 and ordinary series with respect to
and ordinary series with respect to 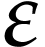 . Given
. Given  and
and  in
in 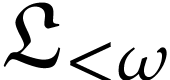 (i.e.
(i.e. 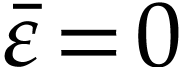 or
or 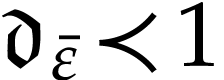 ), one may
then define the substitution
), one may
then define the substitution  of
of 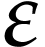 by
by 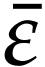 in
in 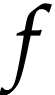 [13,
section 3.4]. The following lemma will be very useful for proving formal
identities in
[13,
section 3.4]. The following lemma will be very useful for proving formal
identities in 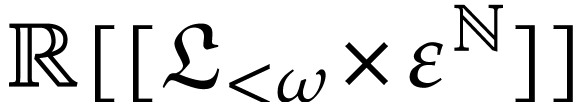 .
.
Proof. Assume for contradiction that 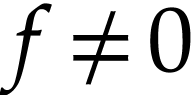 . Write
. Write 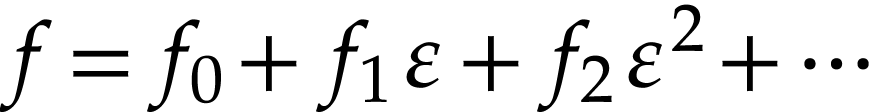 and
let
and
let 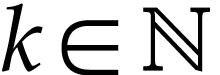 be minimal with
be minimal with 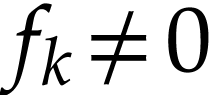 . Since
. Since 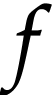 is Noetherian as a
series in
is Noetherian as a
series in 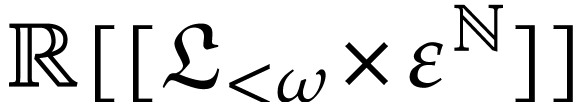 , the set
, the set 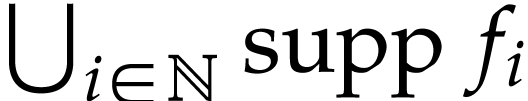 admits a largest element
admits a largest element  .
Taking
.
Taking 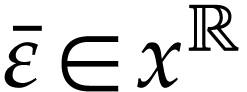 sufficiently small such that
sufficiently small such that 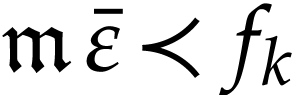 , it follows that
, it follows that 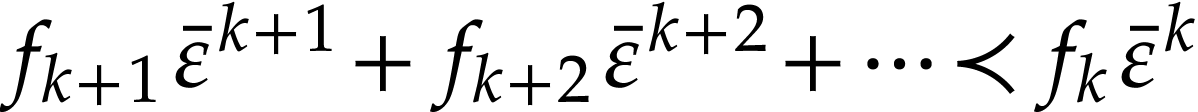 ,
whence
,
whence 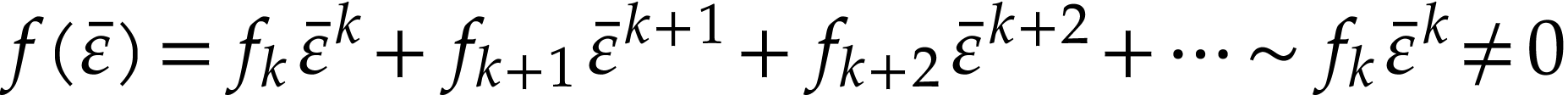 .
.
The following lemma will be used later in order to prove that the
functional inverse 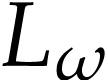 of the function
of the function 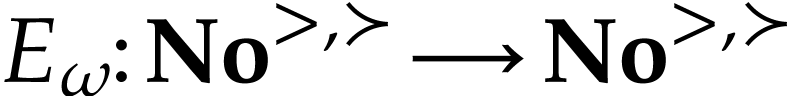 is defined.
is defined.
Proof. The left and right hand sides of (7) are clearly Noetherian series in 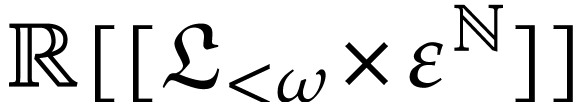 . For any
. For any 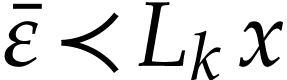 in
in 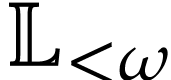 , the following Taylor series expansions hold
[9, Proposition 8.1] in
, the following Taylor series expansions hold
[9, Proposition 8.1] in 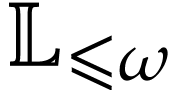 :
:
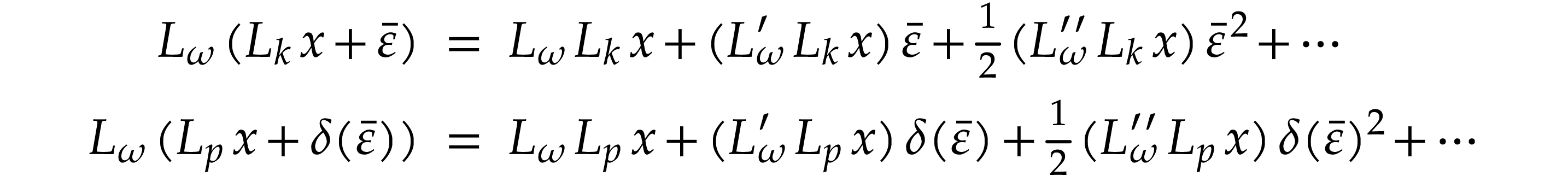
Subtracting both expansions, the identity (7) holds for
 substituted by
substituted by  in
in  . We conclude by Lemma 2.
. We conclude by Lemma 2.
In [9, Section 7], it was shown that there is a
hyperlogarithmic function 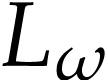 on
on 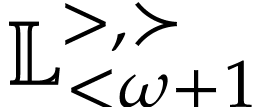 for which
for which 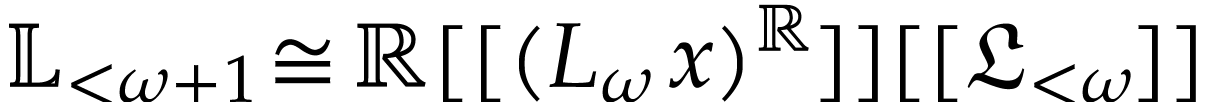 . Let
. Let 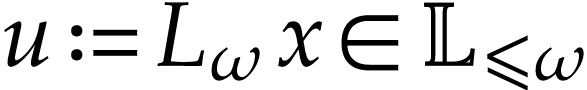 . Then logarithmic transseries in
. Then logarithmic transseries in 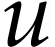 can be considered as elements in
can be considered as elements in 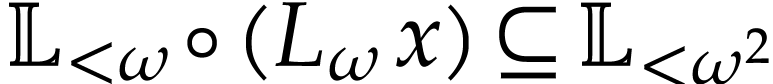 and the successive derivatives of
and the successive derivatives of 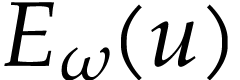 with respect
to
with respect
to 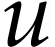 are given by
are given by
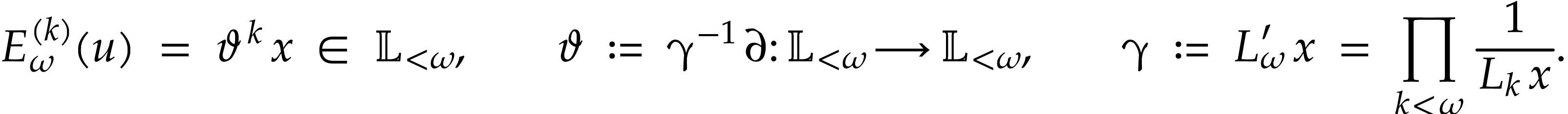
For any 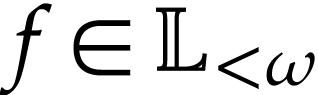 , we have
, we have
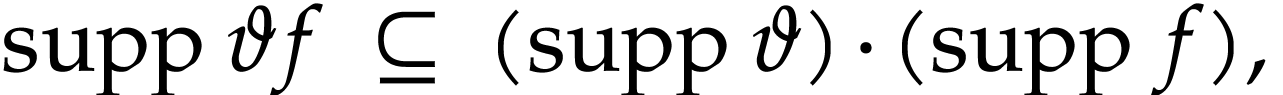
where
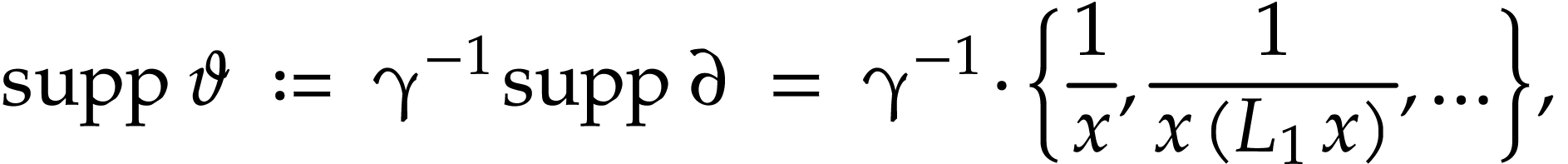
whence
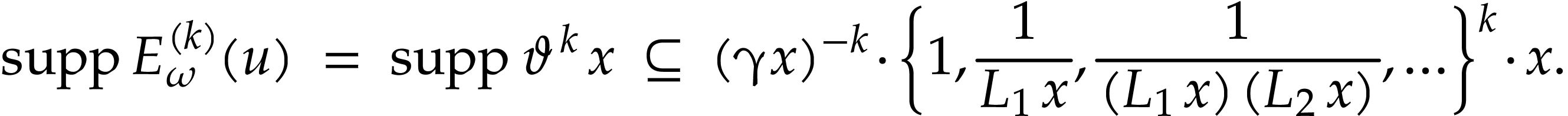
We now give two lemmas that will be used to extend  into a bijective function via Taylor series expansions.
into a bijective function via Taylor series expansions.
Proof. For 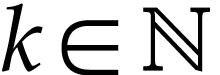 ,
we have
,
we have
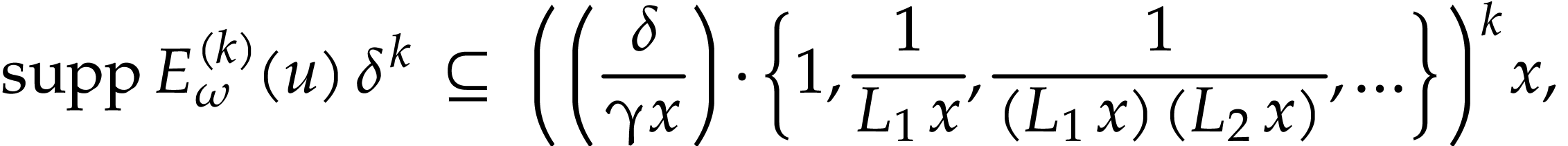
where 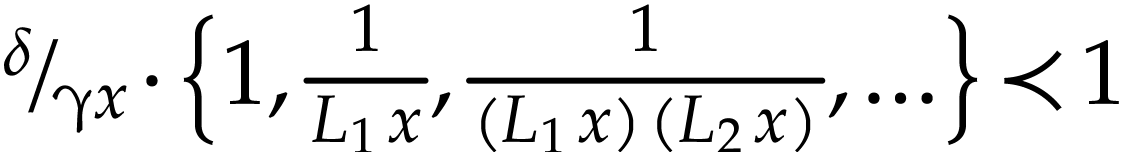 is infinitesimal. It follows from
Neumann's theorems [17, Theorems 3.4 and 3.5] that the sum
is infinitesimal. It follows from
Neumann's theorems [17, Theorems 3.4 and 3.5] that the sum
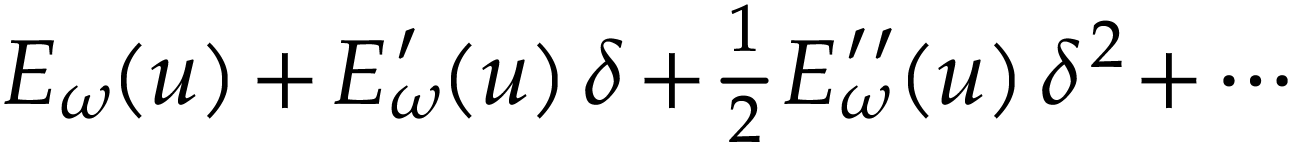 is well-defined.
is well-defined.
Proof. The left hand side is well defined by (8) for 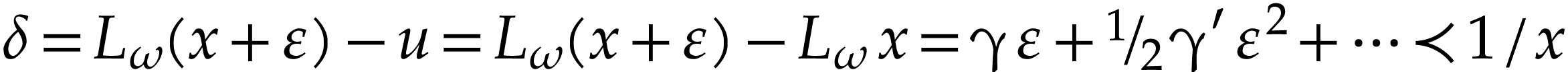 in
in 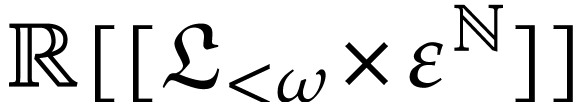 . The fact that (9) holds for
. The fact that (9) holds for  substituted by
substituted by 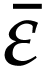 in
in 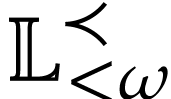 follows from the usual rules of iterated derivatives of functional
inverses. For a detailed proof, we refer to [18, section
6.4]. We conclude by Lemma 2.
follows from the usual rules of iterated derivatives of functional
inverses. For a detailed proof, we refer to [18, section
6.4]. We conclude by Lemma 2.
In this section, we deal with step 1 and 2 of
the definition of  . As
outlined in the introduction, we first define
. As
outlined in the introduction, we first define  on
on
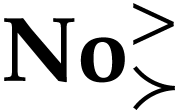 (Proposition 6) and then on
(Proposition 6) and then on  (Proposition 9). This second definition
will require identifying
(Proposition 9). This second definition
will require identifying  and showing that it is
a surreal substructure (Corollary 8) by means of convex
partitions (Proposition 7).
and showing that it is
a surreal substructure (Corollary 8) by means of convex
partitions (Proposition 7).
We first recursively define  for positive purely
infinite numbers
for positive purely
infinite numbers  by
by
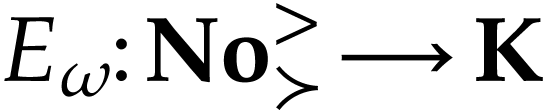 .
Moreover, this cut equation is uniform.
.
Moreover, this cut equation is uniform.
Proof. The function  is
well-defined and strictly increasing by Remark 1. The
uniformity of the equation follows immediately.
is
well-defined and strictly increasing by Remark 1. The
uniformity of the equation follows immediately.
Let 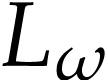 denote the partial inverse function of
denote the partial inverse function of  and prove that
and prove that 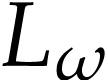 is defined on
is defined on
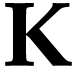 by induction on
by induction on  .
Let
.
Let  such that
such that 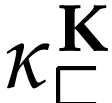 is
contained
is
contained 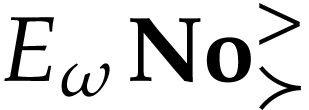 . Since
. Since  is injective, its inverse is defined on
is injective, its inverse is defined on 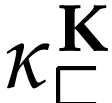 . Let
. Let
This number is well defined since 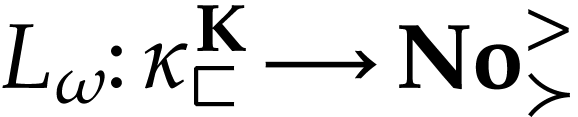 is strictly
increasing and for
is strictly
increasing and for 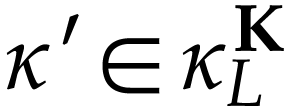 , we have
, we have
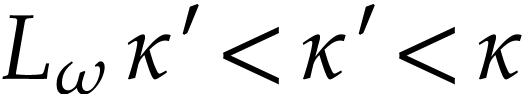 . By uniformity, we have
. By uniformity, we have 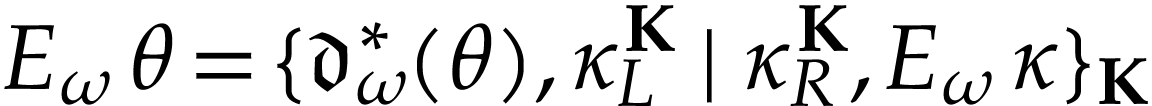 where
where 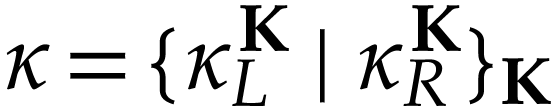 . In
order to conclude that
. In
order to conclude that 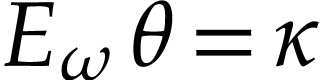 , it
therefore suffices to show that
, it
therefore suffices to show that 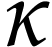 lies in the cut
lies in the cut
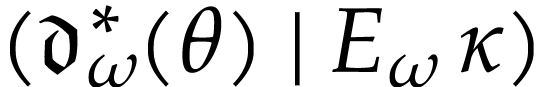 . We have
. We have 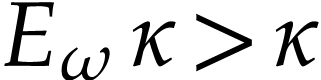 by (10) and
by (10) and 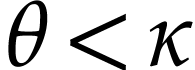 by definition of
by definition of 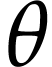 , whence
, whence 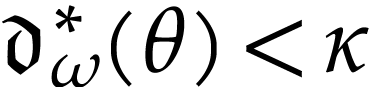 since
since  . We conclude by
induction that
. We conclude by
induction that 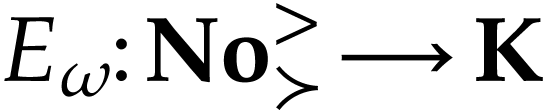 is surjective.
is surjective.
We next identify the class of truncated numbers. For  , we consider the following convex class
, we consider the following convex class
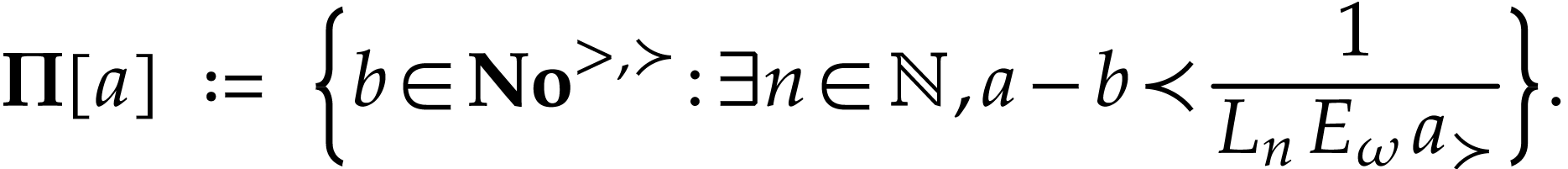
Proof. Given  ,
it is clear that the class
,
it is clear that the class 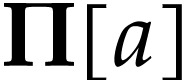 is convex and that it
contains
is convex and that it
contains 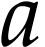 . Note that for
. Note that for
 , we have
, we have 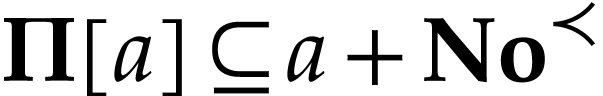 . Let
. Let  with
with 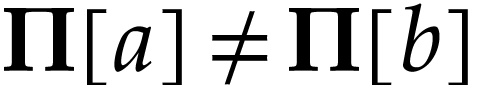 . We claim that
. We claim that 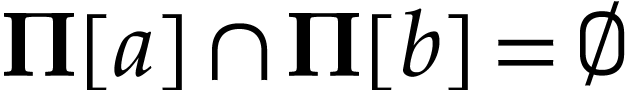 .
If
.
If 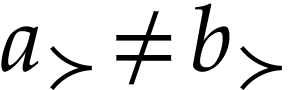 , then we have
, then we have 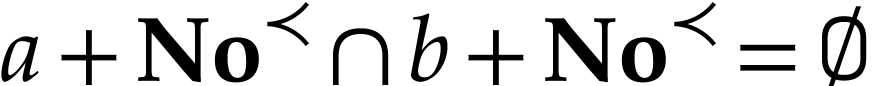 , which yields the result. Assume
that
, which yields the result. Assume
that 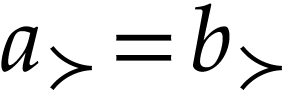 . Assume for
contradiction that there are
. Assume for
contradiction that there are  and
and 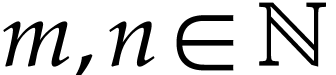 with
with 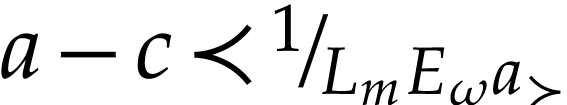 and
and 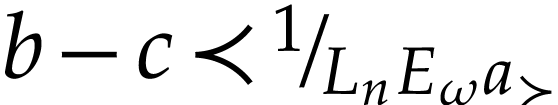 . Given
. Given  ,
there is a number
,
there is a number 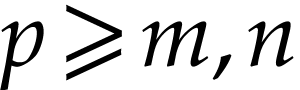 with
with 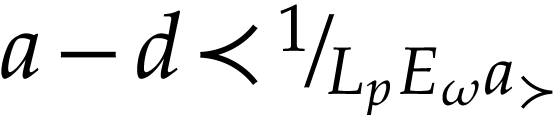 . Therefore
. Therefore 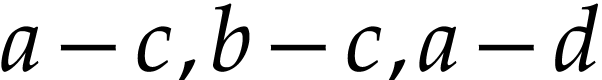 are dominated by
are dominated by
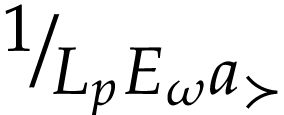 , whence
, whence 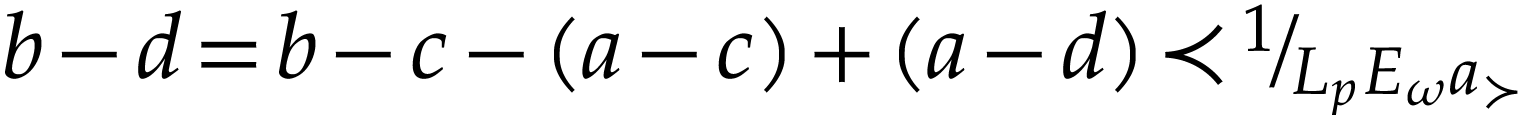 . This proves that
. This proves that 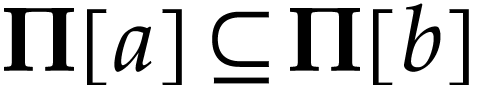 and
symmetric arguments yield
and
symmetric arguments yield 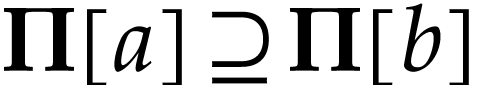 : a
contradiction. This proves our claim. It only remains to see that the
class
: a
contradiction. This proves our claim. It only remains to see that the
class 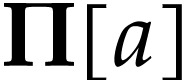 admits a cofinal and coinitial subset for
any
admits a cofinal and coinitial subset for
any  . Indeed, we can take
. Indeed, we can take
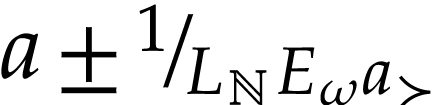 as examples of such sets.
as examples of such sets.
Let  and let
and let  denote the
denote the
 -supremum of truncations
-supremum of truncations 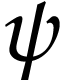 of
of 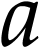 (i.e. series with
(i.e. series with  ) with
) with 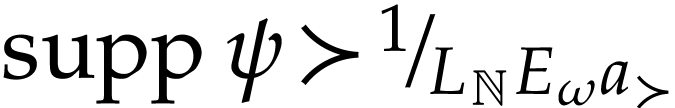 . In particular, we have
. In particular, we have 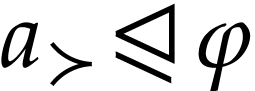 since
since 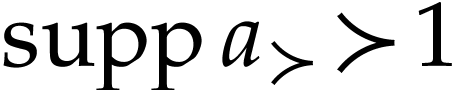 . We see that
. We see that  satisfies
satisfies  and
and 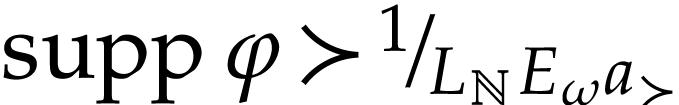 . Write
. Write 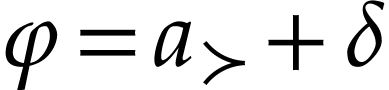 and
and 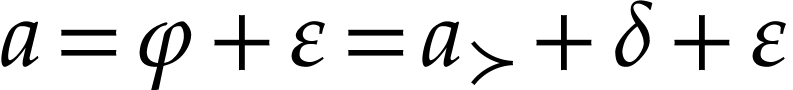 . By
. By  -maximality
of
-maximality
of  , we have
, we have 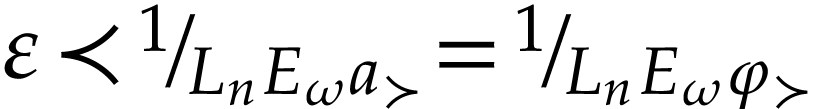 for some
for some  , so
, so  , or equivalently
, or equivalently  .
We deduce that
.
We deduce that  is the
is the  -minimum, hence
-minimum, hence  -minimum
of
-minimum
of  , so
, so  . We also see that for
. We also see that for  and
and 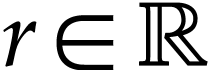 , we have
, we have 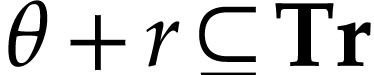 . Since
. Since  is a surreal
substructure, we may recursively define
is a surreal
substructure, we may recursively define 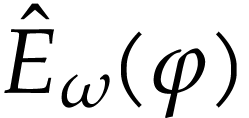 for
for  by
by
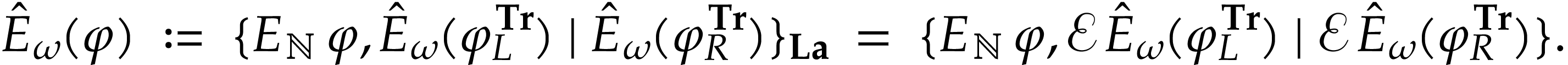 |
(11) |
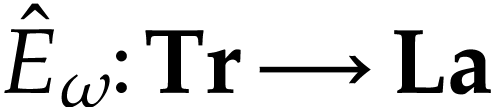 is strictly increasing.
is strictly increasing.
Proof. Since  is a
surreal substructure, the definition, strict monotonicity and uniformity
follow by Remark 1. For
is a
surreal substructure, the definition, strict monotonicity and uniformity
follow by Remark 1. For  ,
we have
,
we have 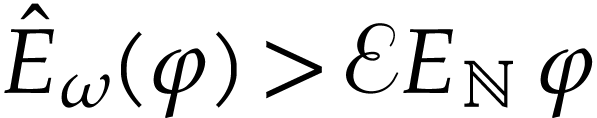 since
since  on
on  . We deduce that
. We deduce that 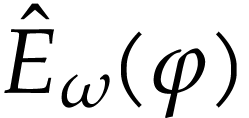 is
is  -simple, hence
log-atomic.
-simple, hence
log-atomic.
We now show that 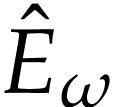 satisfies the functional
equation (1). By [4, Lemma 2.4], for every
infinite monomial
satisfies the functional
equation (1). By [4, Lemma 2.4], for every
infinite monomial  , we have
, we have
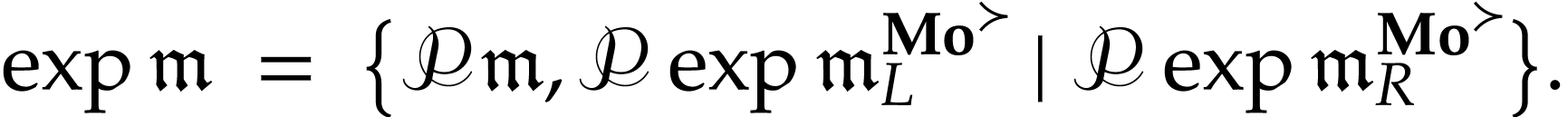 |
(12) |
Proof. We prove this by induction on 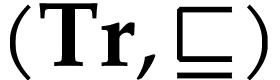 . Let
. Let  such
that this holds on
such
that this holds on 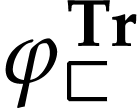 . Note
that
. Note
that 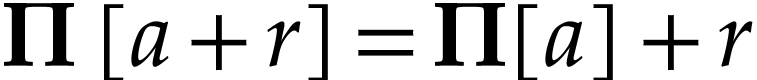 for all
for all  and
and 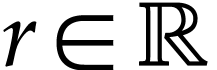 . We have
. We have  , so
, so
We deduce that
Since 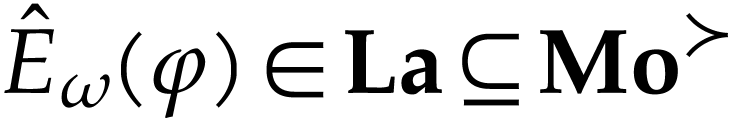 , we may apply (12). We also note that
, we may apply (12). We also note that 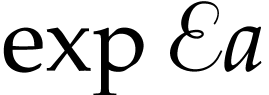 and
and 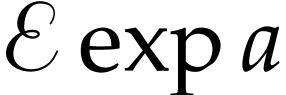 are mutually cofinal and coinitial for all
are mutually cofinal and coinitial for all  to obtain
to obtain
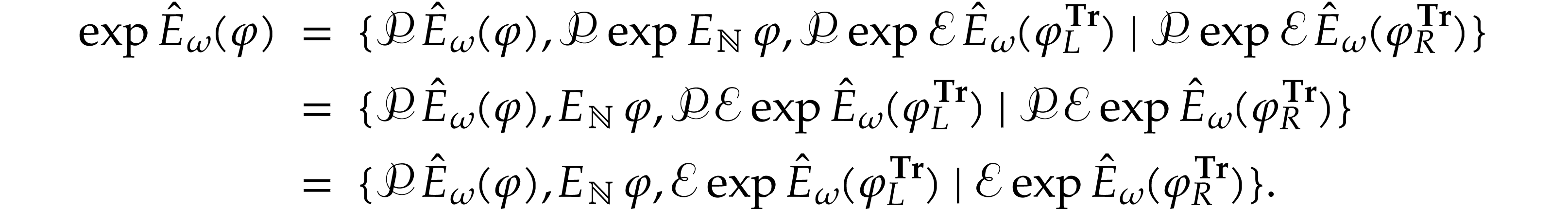
We have 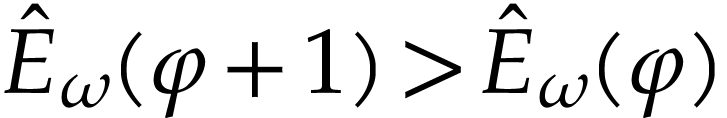 , so
, so 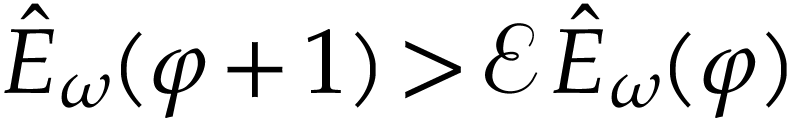 and
and 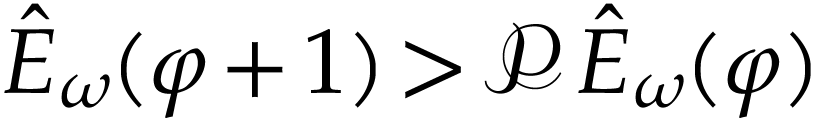 . We clearly have
. We clearly have 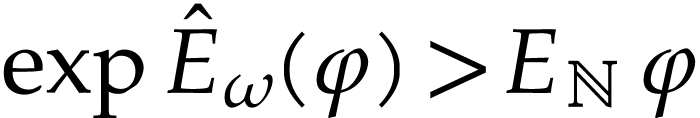 . We deduce that
. We deduce that 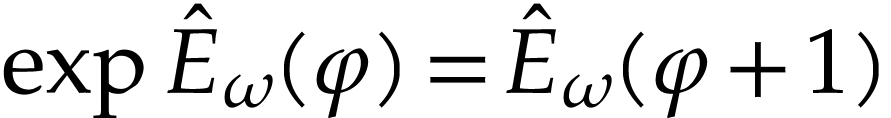 . By induction, the relation is valid on
. By induction, the relation is valid on  .
.
It remains to check that the function  extends
extends
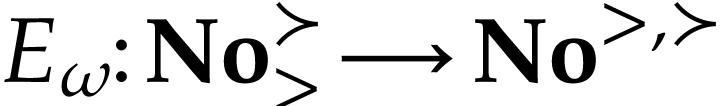 .
.
 , we have
, we have
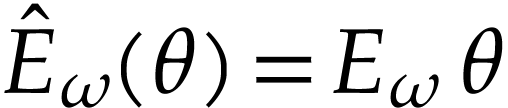 .
.
Proof. We prove this by induction on 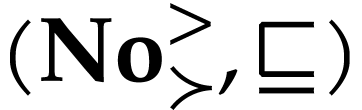 . Let
. Let  be
such that this holds on
be
such that this holds on 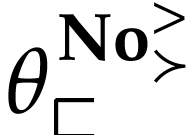 . For
. For
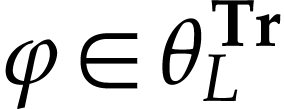 , we have
, we have 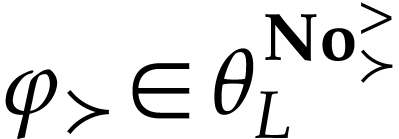 , and there is
, and there is  with
with
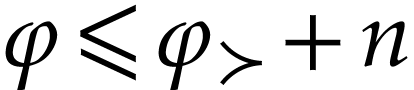 . We deduce that
. We deduce that 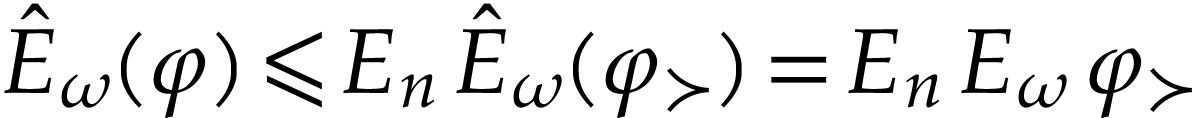 . In particular, we have
. In particular, we have 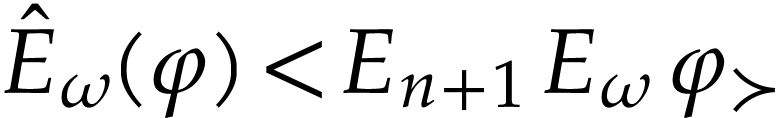 so
so 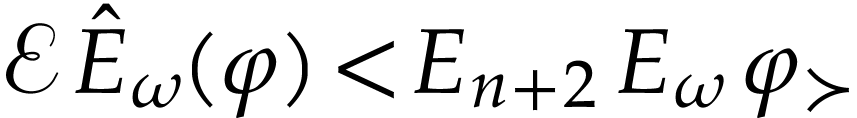 . This proves that
. This proves that 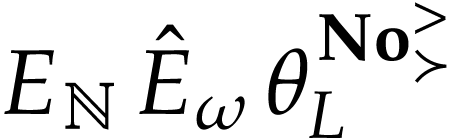 is cofinal with respect to
is cofinal with respect to 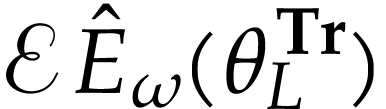 . For
. For 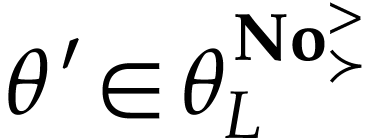 and
and  , we have
, we have 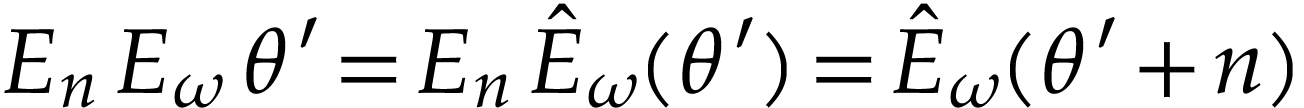 where
where 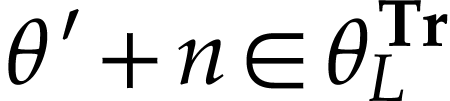 , so
, so 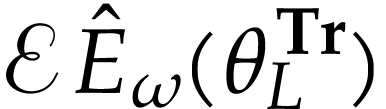 is
cofinal with respect to
is
cofinal with respect to 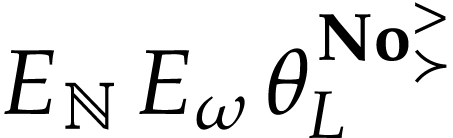 .
Symmetric arguments yield that
.
Symmetric arguments yield that 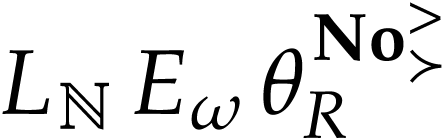 and
and 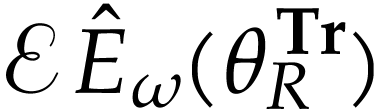 are mutually coinitial. We conclude that
are mutually coinitial. We conclude that 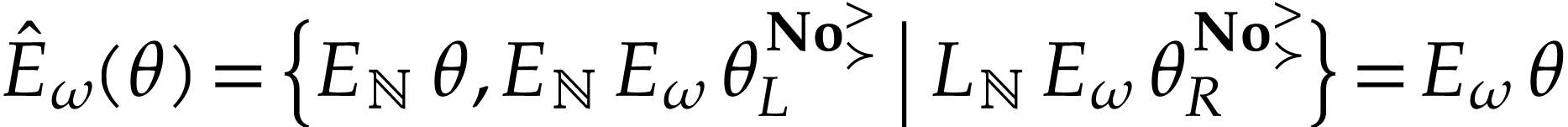 .
.
Since 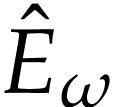 and
and  agree on
agree on  , we will identify both functions
hereafter and simply write
, we will identify both functions
hereafter and simply write  instead of
instead of 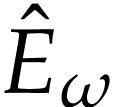 . Let us finally examine its
functional inverse
. Let us finally examine its
functional inverse 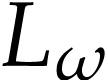 .
.
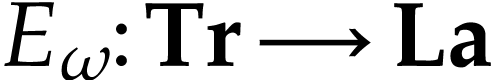 is bijective. Its
functional inverse
is bijective. Its
functional inverse 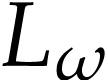 satisfies the following
uniform cut equation on
satisfies the following
uniform cut equation on 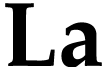 :
:
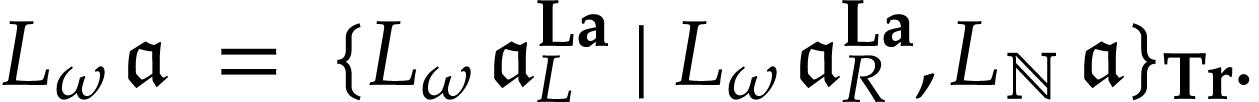
Proof. Noting that 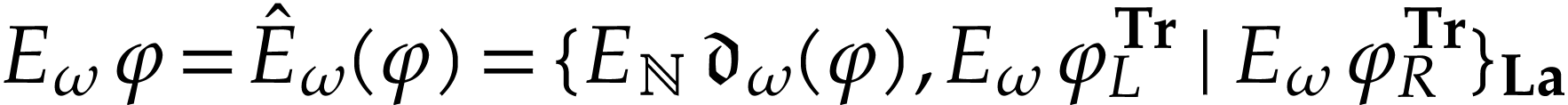 for
all
for
all  , it suffices to show
that
, it suffices to show
that 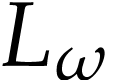 is strictly increasing and its cut equation
is uniform, which follows from the same arguments as in Proposition 6.
is strictly increasing and its cut equation
is uniform, which follows from the same arguments as in Proposition 6.
In this section, we complete the final step 3 of the
definition of  , by extending
its domain to the whole class
, by extending
its domain to the whole class 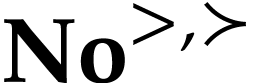 .
The field
.
The field 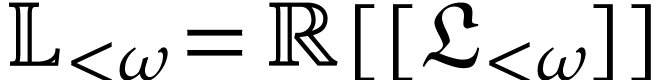 of logarithmic hyperseries of [9] is a subfield of the class of all well-based transseries in
an infinitely large variable
of logarithmic hyperseries of [9] is a subfield of the class of all well-based transseries in
an infinitely large variable 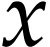 .
Both
.
Both  and the class of all transseries are closed
under derivation and under composition [10, 12,
18]. For every positive infinite number
and the class of all transseries are closed
under derivation and under composition [10, 12,
18]. For every positive infinite number  , there also exists an evaluation embedding
, there also exists an evaluation embedding
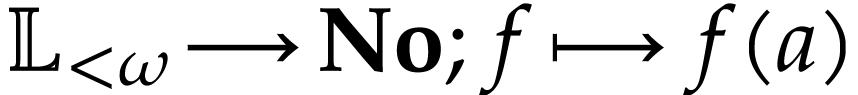 such that
such that 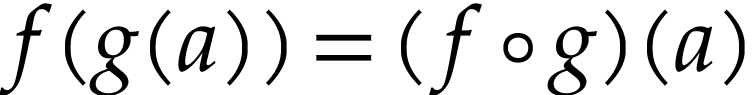 for all
for all 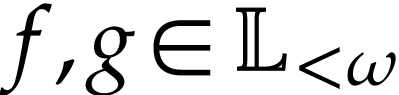 : see [5].
: see [5].
Given  , let
, let 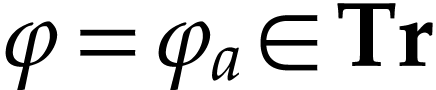 be the unique truncated series with
be the unique truncated series with  .
If
.
If 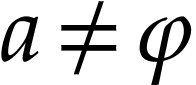 , then there is a smallest
number
, then there is a smallest
number 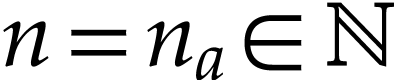 with
with
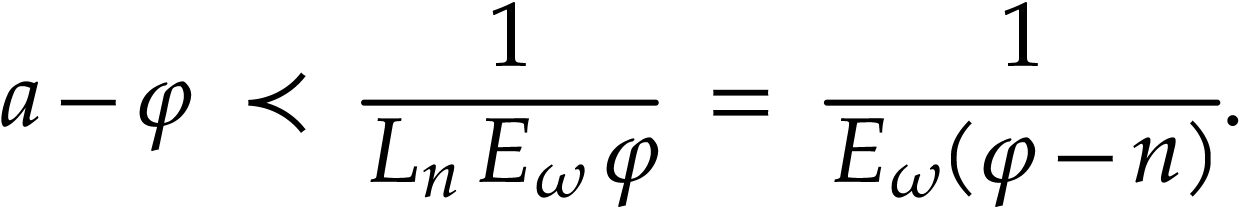
Write 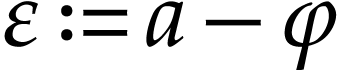 . With
. With 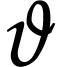 as in section 3, we define for every
as in section 3, we define for every  :
:
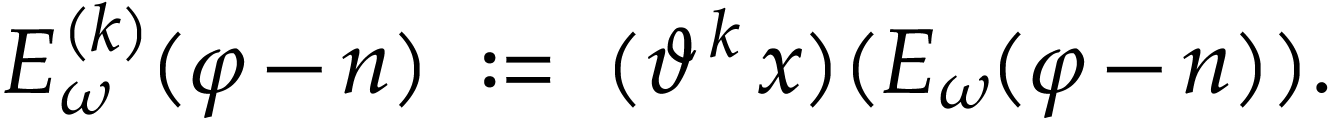
Substitution of 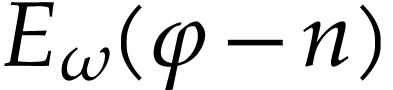 for
for 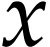 in
(8) allows us to extend the definition of
in
(8) allows us to extend the definition of  by
by
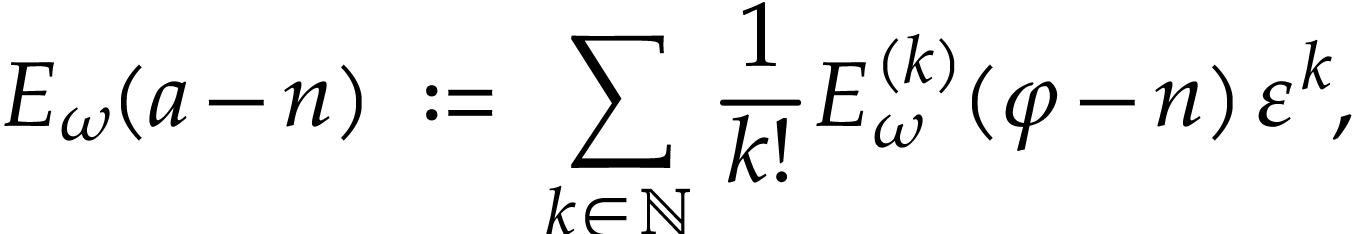 |
(13) |
and
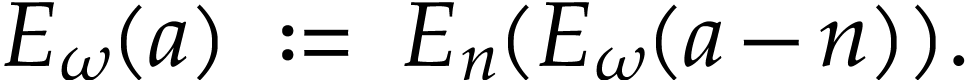
Let us first check (1) for this extended definition.
Proof. If 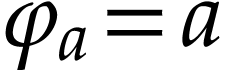 ,
then this is Proposition 10. Otherwise, we have
,
then this is Proposition 10. Otherwise, we have 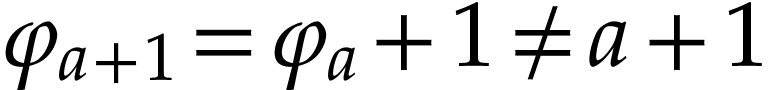 and
and 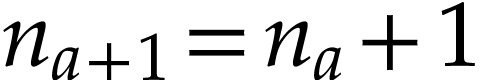 , whence
, whence
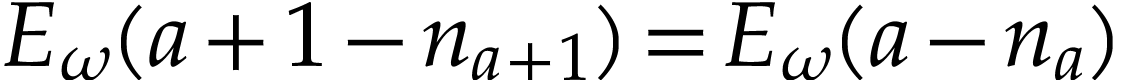 and
and
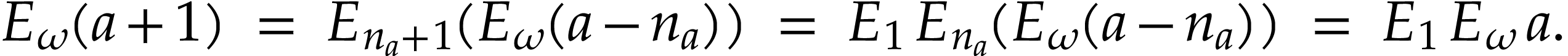

Inversely, consider an arbitrary positive infinite number  . Then there exists a
. Then there exists a 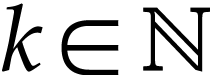 such that
such that  for some log-atomic
for some log-atomic  and
and 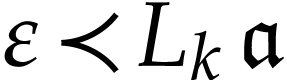 [4, Corollary 5.11]. We extend
the definition of
[4, Corollary 5.11]. We extend
the definition of 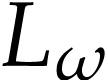 to any such number
to any such number 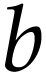 by
by
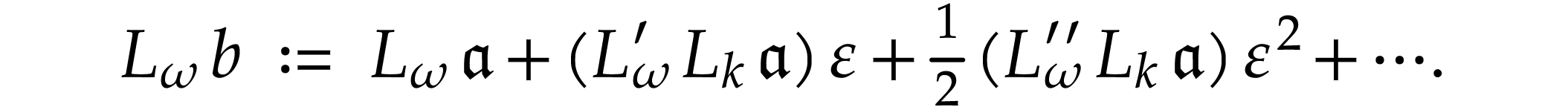
In view of Lemma 3, the value of 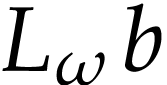 does not depend on the choice of
does not depend on the choice of 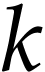 .
Note also that this definition indeed extends our previous definition of
.
Note also that this definition indeed extends our previous definition of
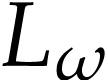 on
on  ,
since
,
since 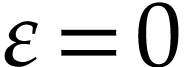 when
when  .
.
In order to prove that the extended functions 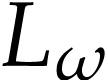 and
and  are functional inverses of each other, we
first check that
are functional inverses of each other, we
first check that 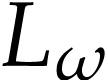 satisfies the
“inverse” of the functional equation (1).
satisfies the
“inverse” of the functional equation (1).
Proof. With 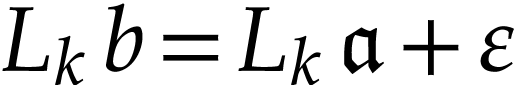 as above
(while taking
as above
(while taking 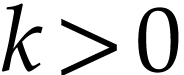 ), we have
), we have
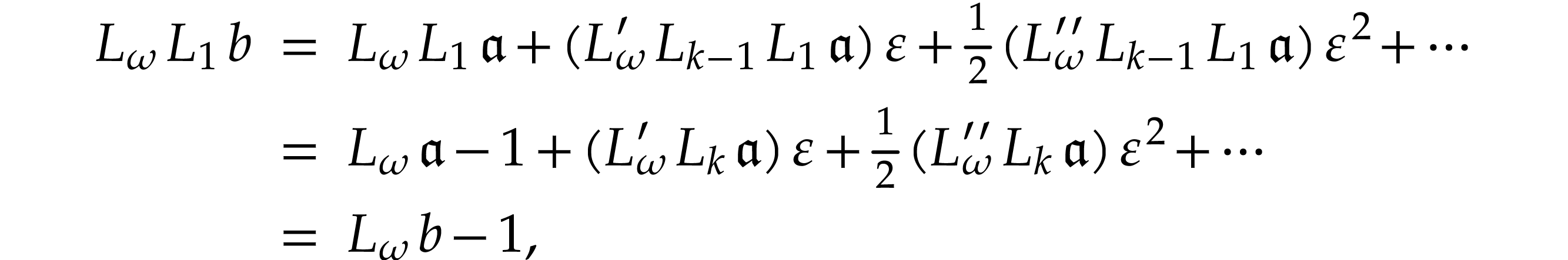
where 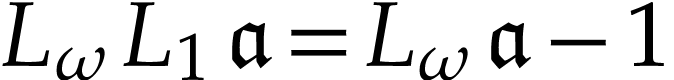 because of Proposition 10.
because of Proposition 10.
 , we
have
, we
have 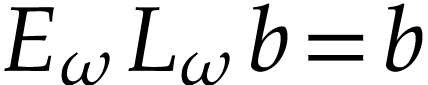 .
.
Proof. Let  be such that
be such that
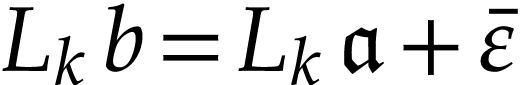 , where
, where  and
and 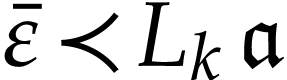 . Let us first consider
the special case when
. Let us first consider
the special case when 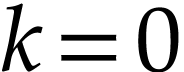 . Since
. Since
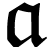 is log-atomic, we have
is log-atomic, we have 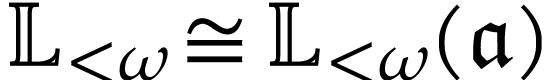 . From Lemma 5, it therefore follows
that
. From Lemma 5, it therefore follows
that 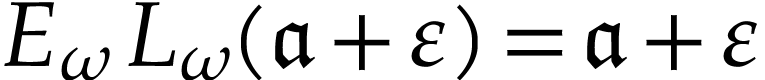 inside
inside 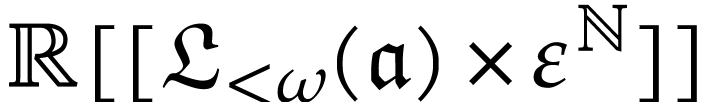 .
The result follows by specializing this relation at
.
The result follows by specializing this relation at 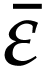 . If
. If 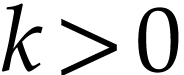 ,
then
,
then 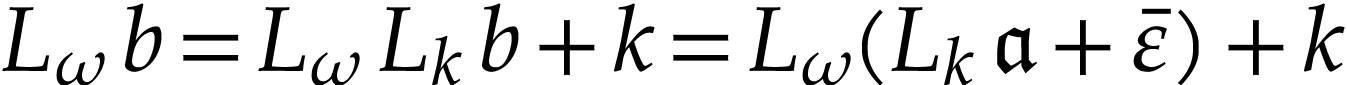 by Proposition 14. Applying
the result for the special case when
by Proposition 14. Applying
the result for the special case when 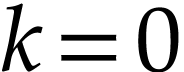 ,
we have
,
we have 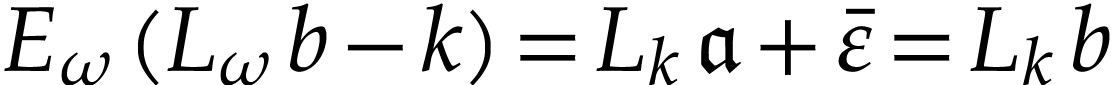 . We conclude by
Proposition 13.
. We conclude by
Proposition 13.
In particular, the function 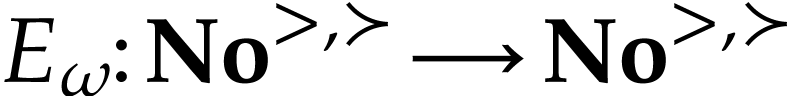 is surjective. We
next prove that it is strictly increasing, concluding our proof that
is surjective. We
next prove that it is strictly increasing, concluding our proof that
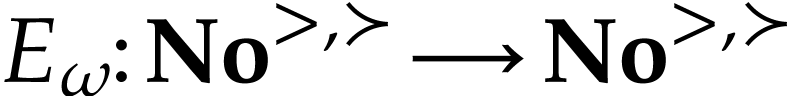 is a strictly increasing bijection with
functional inverse
is a strictly increasing bijection with
functional inverse 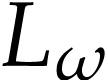 . For
this, we need two lemmas.
. For
this, we need two lemmas.
Proof. Note that 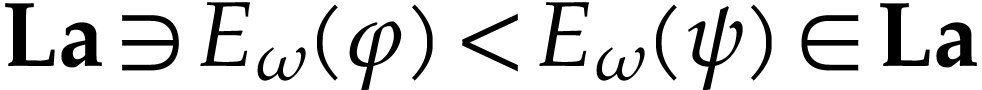 ,
so it is enough to prove that
,
so it is enough to prove that 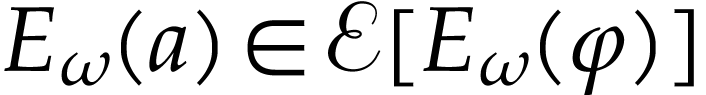 for all
for all  . For such
. For such 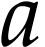 , there is
, there is  with
with 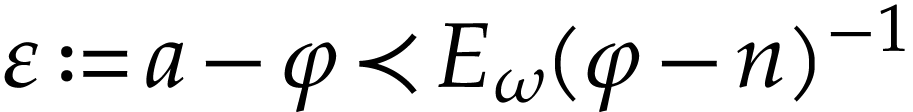 , and
, and
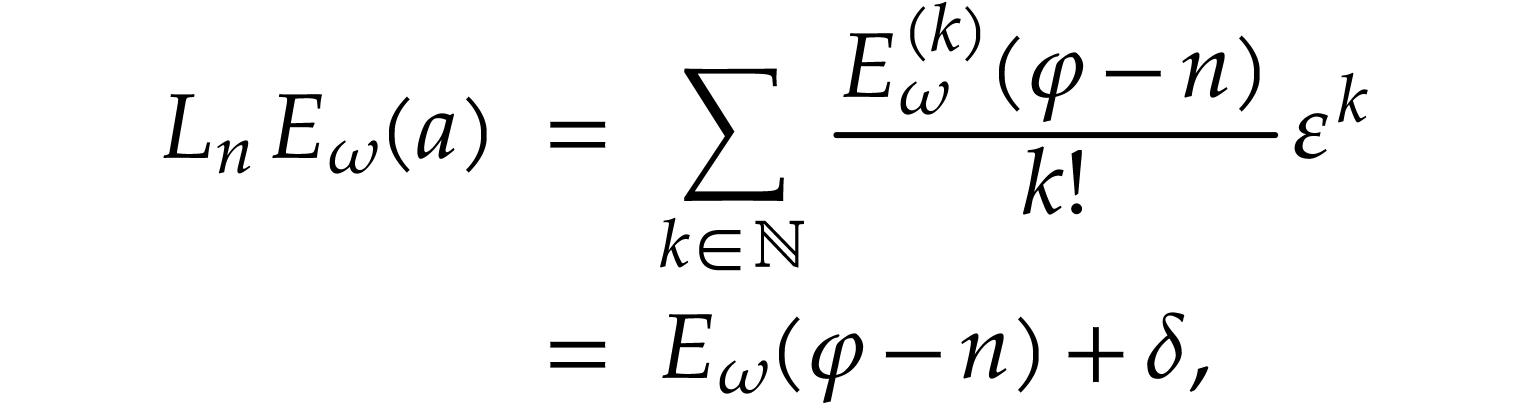
where 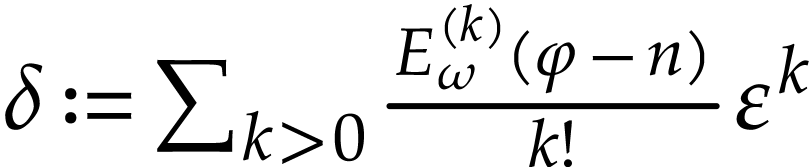 is infinitesimal. So
is infinitesimal. So 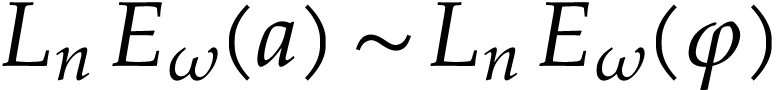 , whence
, whence 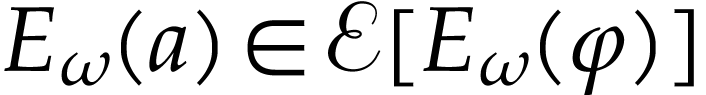 .
.
Proof. Write 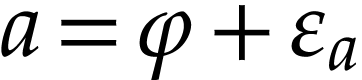 and
and 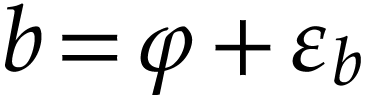 where
where 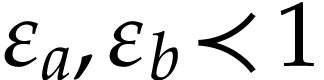 and let
and let  with
with 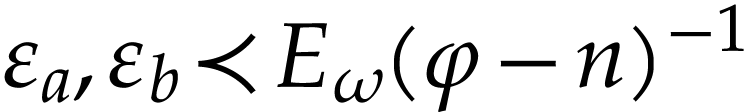 . Writing
. Writing
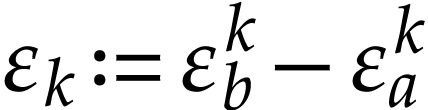 for
for 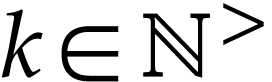 ,
we have
,
we have 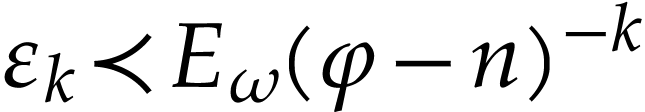 . We deduce that
. We deduce that
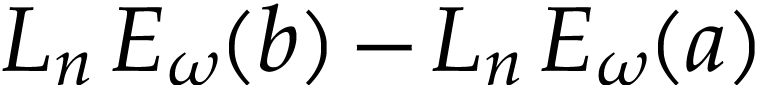 |
 |
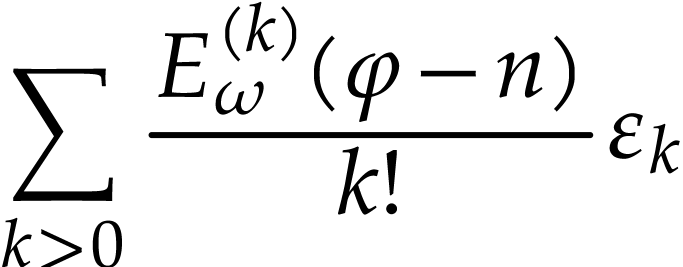 |
|
 |
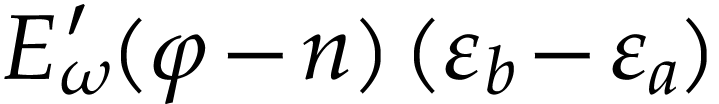 |
||
 |
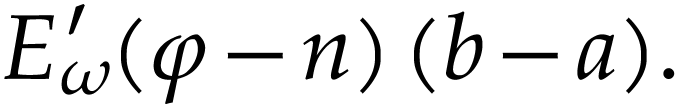 |
 |
 is strictly increasing
on
is strictly increasing
on  .
.
Proof. Let  with
with 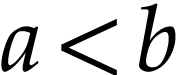 . If
. If 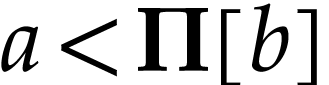 ,
then we get
,
then we get 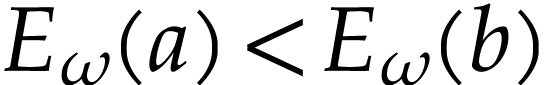 by Lemma 16. Otherwise,
we have
by Lemma 16. Otherwise,
we have 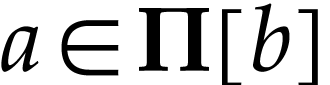 so by Lemma 17, there are
so by Lemma 17, there are
 and
and  with
with
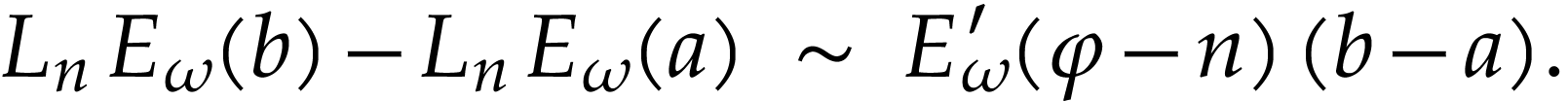
Since 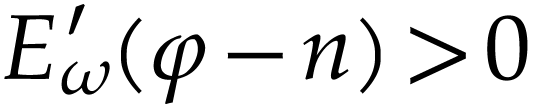 , we conclude that
, we conclude that
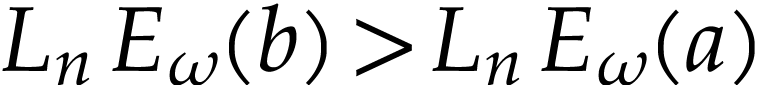 , whence
, whence 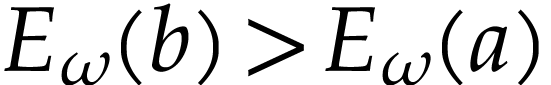 .
.
 is bijective, with
functional inverse
is bijective, with
functional inverse 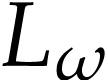 .
.

We conclude this paper by showing that  is the
simplest well-behaved solution to (1) in a sense that will
be made precise. Let us first show that
is the
simplest well-behaved solution to (1) in a sense that will
be made precise. Let us first show that  is
surreal-analytic. Generalizing (13), we let
is
surreal-analytic. Generalizing (13), we let 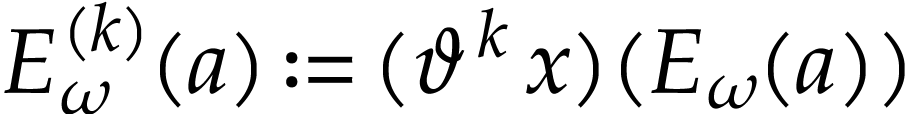 for all
for all  and
and 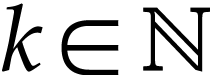 .
.
 and
and  with
with 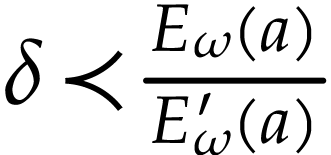 , the sum
, the sum 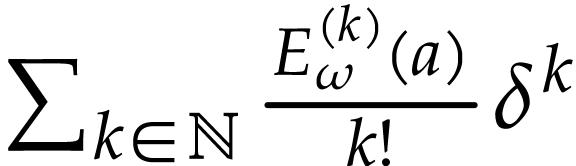 converges to
converges to 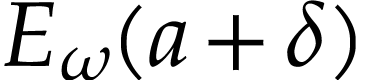 .
.
Proof. Let 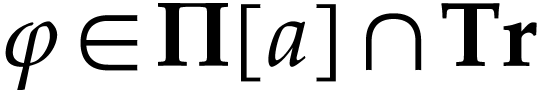 .
Assume first that
.
Assume first that 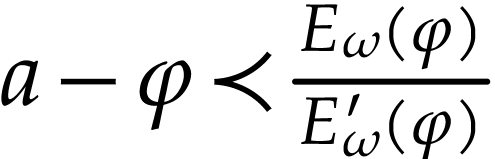 . We rely
on the notion of horizontal saturation of Taylor families from [18,
section 6.2.2]. The restrictions
. We rely
on the notion of horizontal saturation of Taylor families from [18,
section 6.2.2]. The restrictions 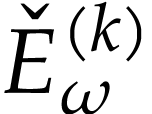 of the
functions
of the
functions 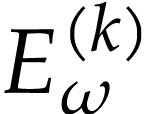 to
to  form a
Taylor family with index
form a
Taylor family with index 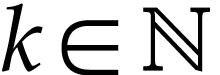 .
Indeed, for
.
Indeed, for  with
with 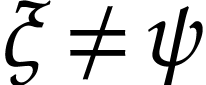 ,
we have
,
we have 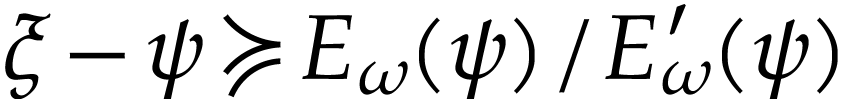 , so the family
, so the family 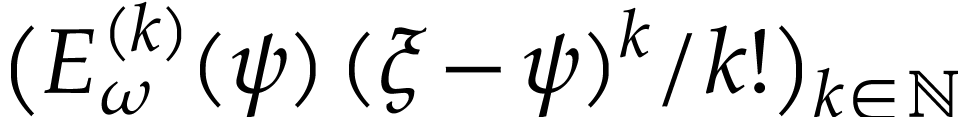 is not summable. By [18, Proposition
6.2.4], the family
is not summable. By [18, Proposition
6.2.4], the family 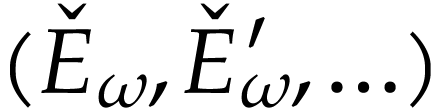 has a minimal horizontally
saturated expansion
has a minimal horizontally
saturated expansion 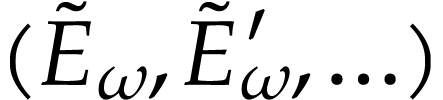 . The
domain of
. The
domain of 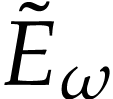 in particular contains the class of
numbers
in particular contains the class of
numbers 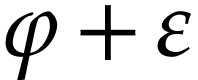 with
with  and
and 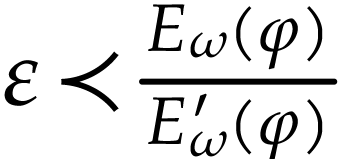 . Given such a number
. Given such a number 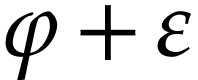 , we have
, we have
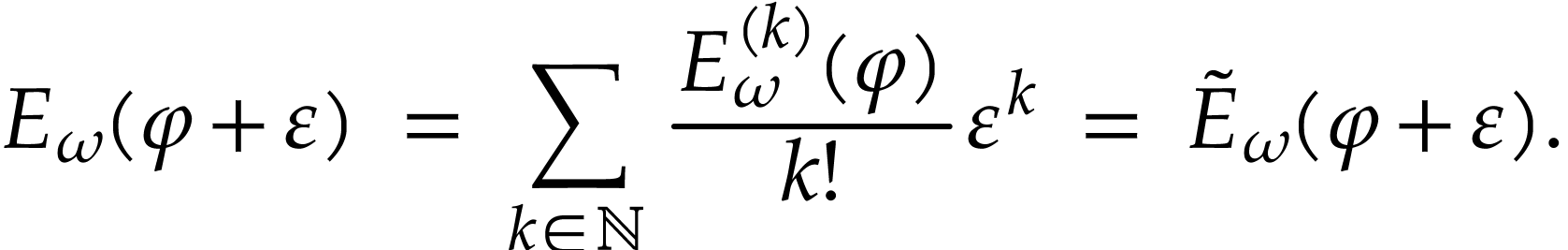
Indeed, the first equality holds by definition (since 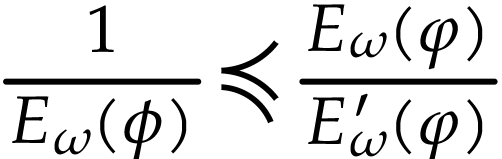 ), and the second one by horizontal saturation.
In particular, this yields
), and the second one by horizontal saturation.
In particular, this yields 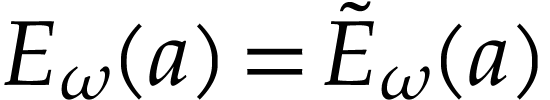 and
and 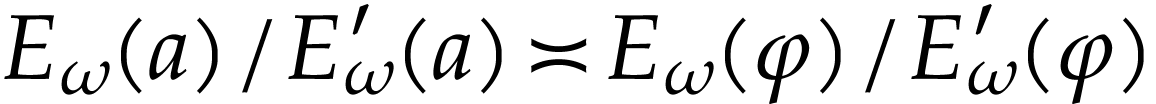 . For
. For 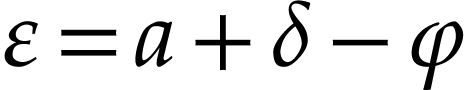 ,
it follows that
,
it follows that
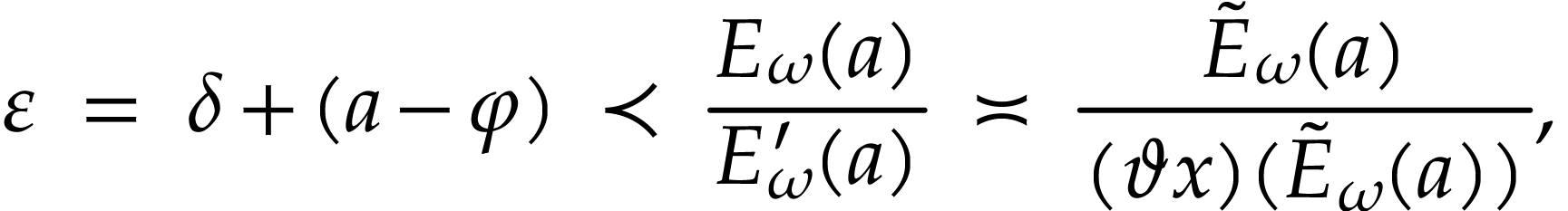
so the sum 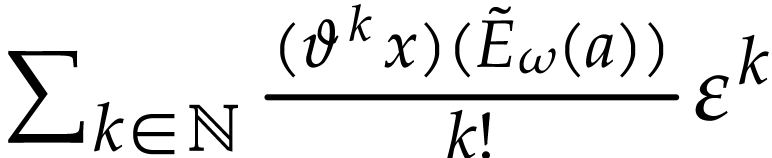 converges as in (13). By
horizontal saturation, we get
converges as in (13). By
horizontal saturation, we get
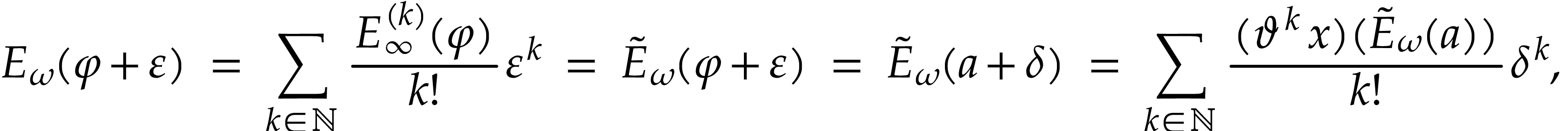
whence
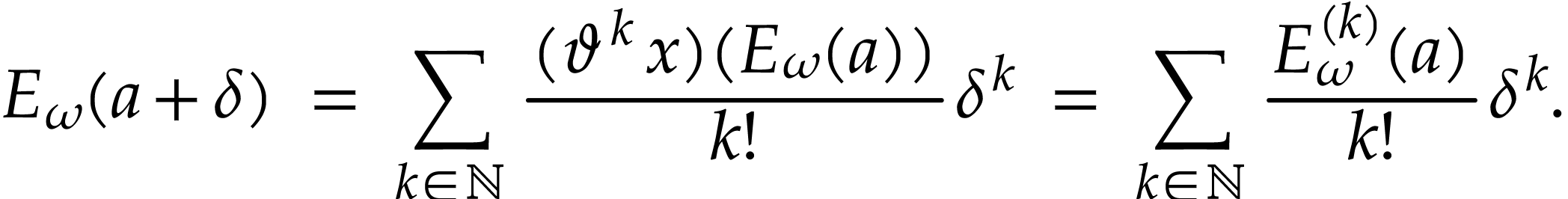
This concludes the proof in the special case when 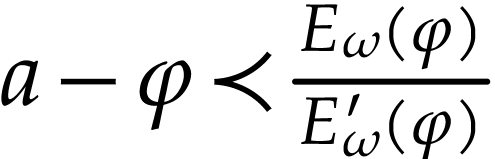 .
.
In general, let  be minimal with
be minimal with 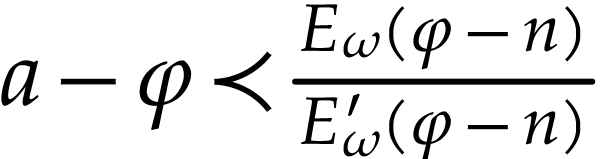 . We will prove the result by induction on
. We will prove the result by induction on
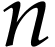 . In view of the special
case, we have
. In view of the special
case, we have
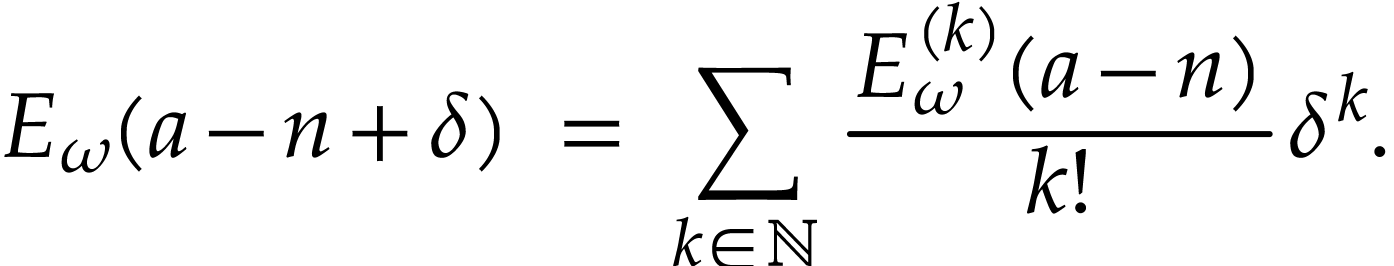
Now assume that 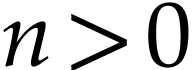 and let
and let 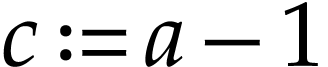 . Then
. Then
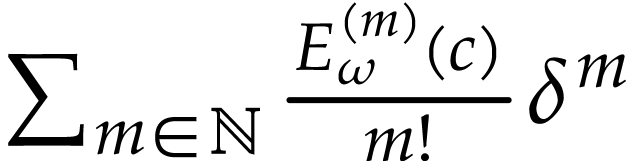 converges to
converges to 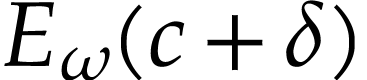 by the
induction hypothesis.
by the
induction hypothesis.
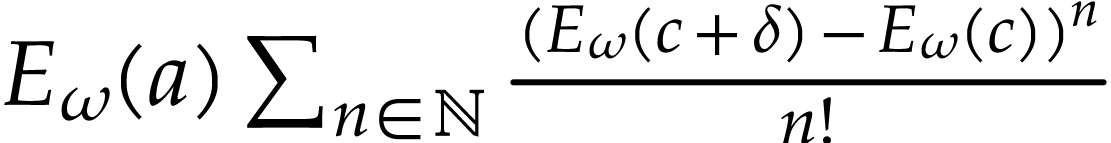 converges to
converges to 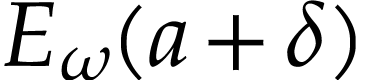 ,
by using the Taylor expansion of
,
by using the Taylor expansion of 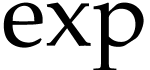 at
at 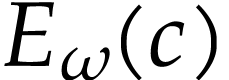 and the fact that
and the fact that
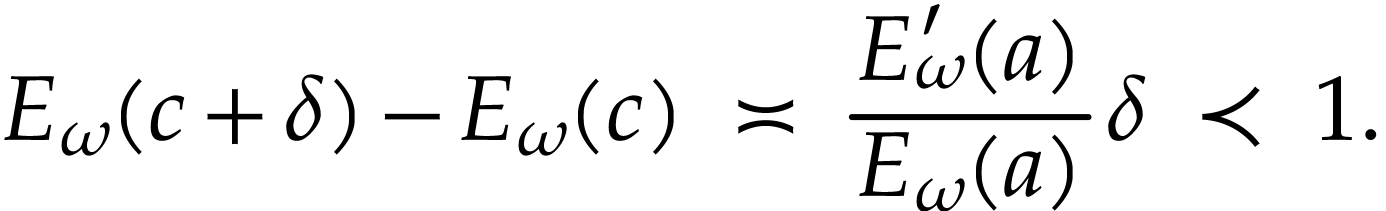
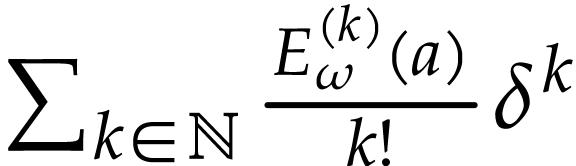 converges, since
converges, since 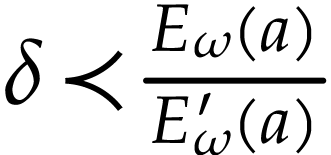 .
.
For  and
and 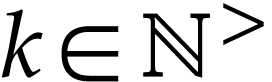 ,
let
,
let
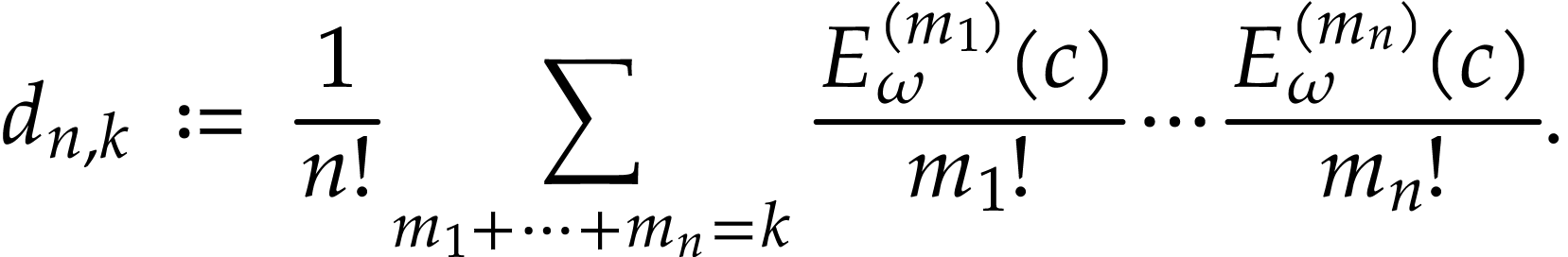
As in the proof of [5, Proposition 3.16], it is enough to justify the convergence of the sum
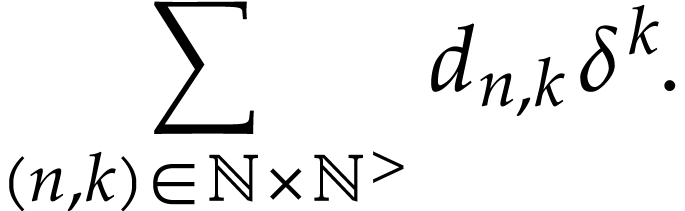
But this directly follows from the fact that
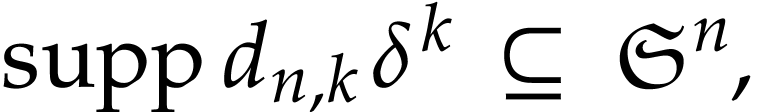
where the set
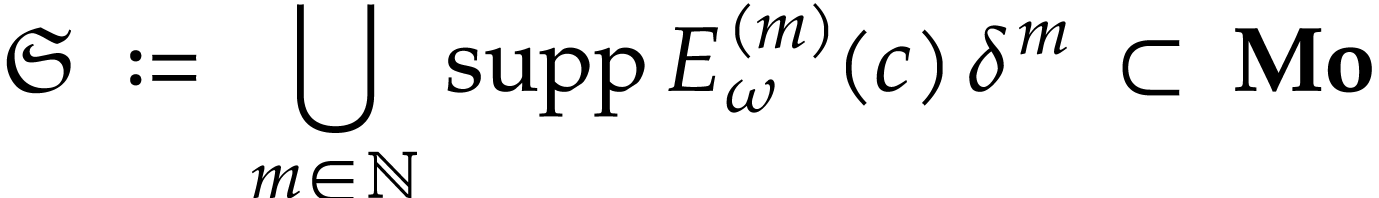
is well-based and infinitesimal.
Let us now introduce the notion of simplicity for surreal-valued functions.
 be a subclass of
be a subclass of
 and let
and let  be a class of
functions
be a class of
functions  . We say that a
function
. We say that a
function  is simplest
if for any
is simplest
if for any 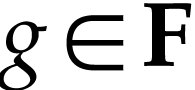 with
with 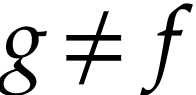 and
for any
and
for any  -minimal
-minimal 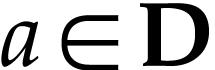 with
with 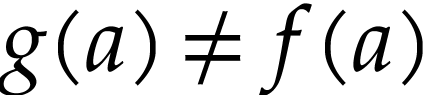 , we
have
, we
have 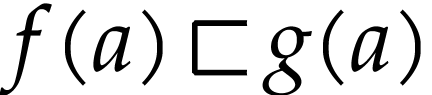 .
.
The above definition was first introduced in [4] in order
to show the existence of a “simplest pre-derivation” on
surreal numbers. By definition, if there is a simplest function in 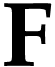 , then it is unique. We can now
formulate our main result about the simplicity of our solution
, then it is unique. We can now
formulate our main result about the simplicity of our solution  to (1).
to (1).
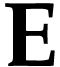 be the class of functions
be the class of functions  such that
such that
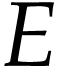 is strictly increasing.
is strictly increasing.
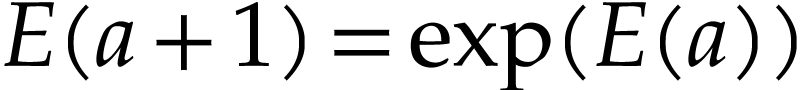 for all
for all  .
.
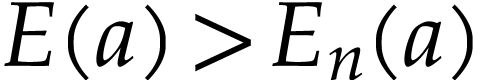 for all
for all  and
and  .
.
For  and
and  with
with 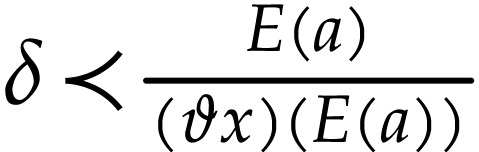 , the sum
, the sum 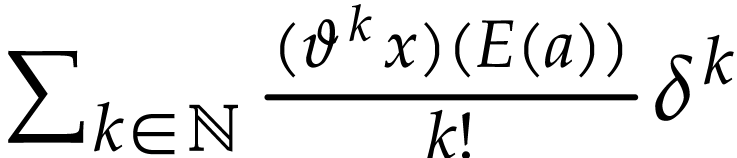 converges to
converges to 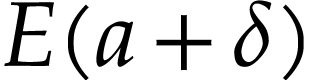 .
.
Then  is the simplest element of
is the simplest element of 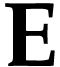 .
.
Proof. Let  be such that
be such that
 and let
and let  be simplest with
be simplest with
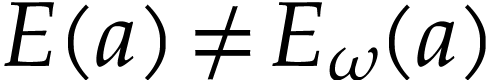 . Given
. Given  and
and 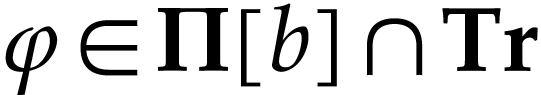 with
with 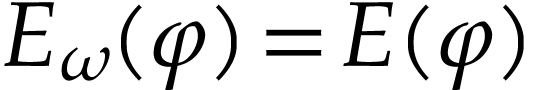 ,
we have
,
we have 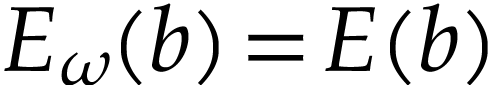 , by (
, by (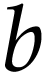 ) and (
) and (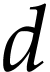 ).
Taking
).
Taking 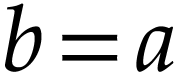 and
and 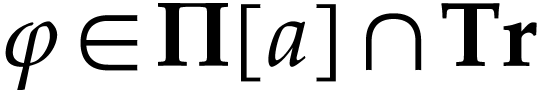 with
with 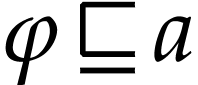 , this implies that
, this implies that 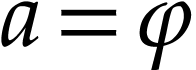 , i.e.
, i.e. 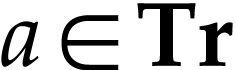 .
.
Since 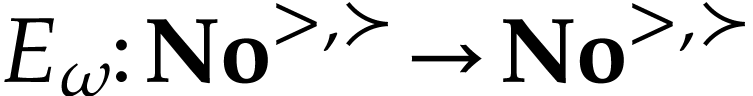 is strictly increasing and surjective, the
classes
is strictly increasing and surjective, the
classes 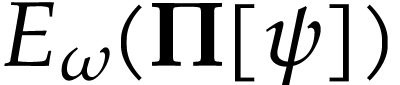 with
with  form a
convex partition of
form a
convex partition of  . Since
. Since
 is injective with
is injective with 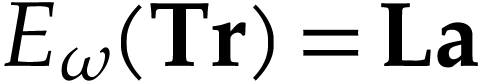 ,
we have
,
we have 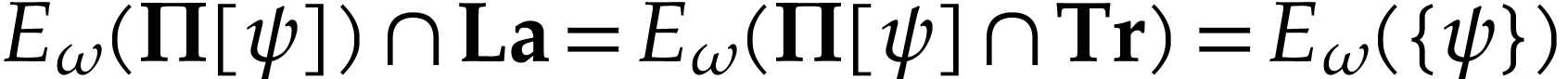 . We claim that
. We claim that 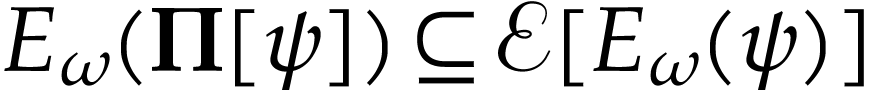 . Assume for contradiction that
there is
. Assume for contradiction that
there is  with
with 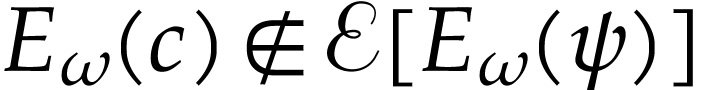 .
By convexity of
.
By convexity of 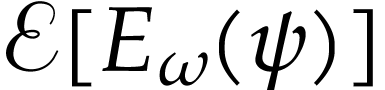 , we have
, we have
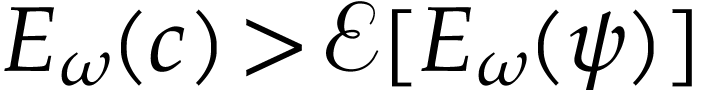 or
or 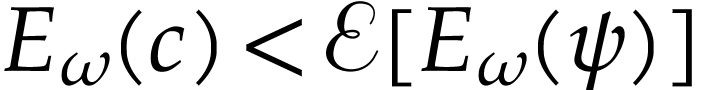 .
Set
.
Set 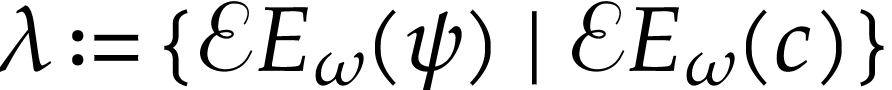 in the first case and
in the first case and 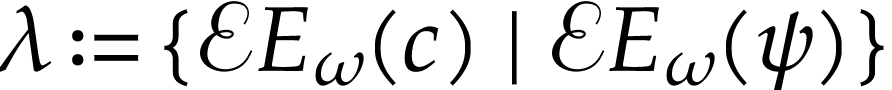 in the second case. In both cases, we get
in the second case. In both cases, we get  .
Since
.
Since 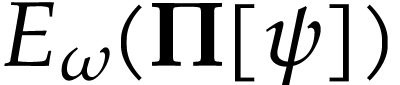 is convex, we also have
is convex, we also have 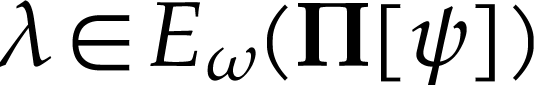 . But then
. But then 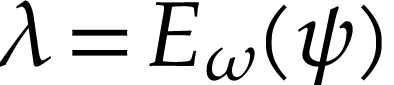 ,
since
,
since 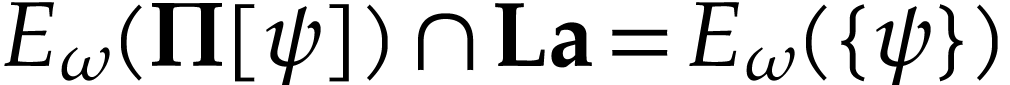 ; a contradiction.
Applying similar arguments to
; a contradiction.
Applying similar arguments to 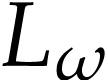 instead of
instead of  , one obtains
, one obtains 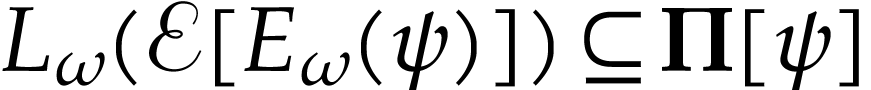 , whence
, whence 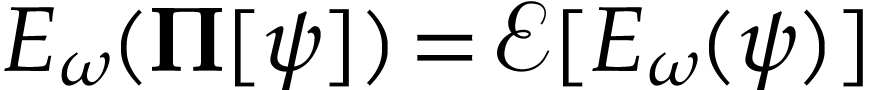 .
.
Let 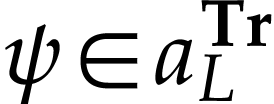 . We have
. We have 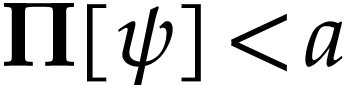 because
because 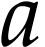 and
and 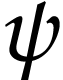 are
are  -simple. The previous
argument and
-simple. The previous
argument and 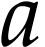 ) yield
) yield 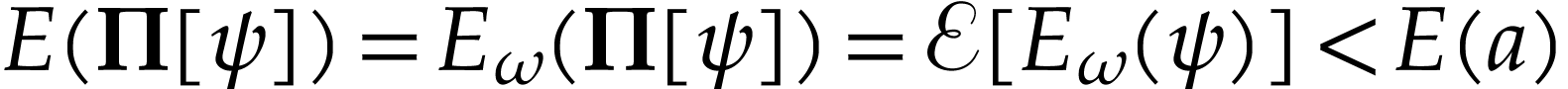 . So
. So 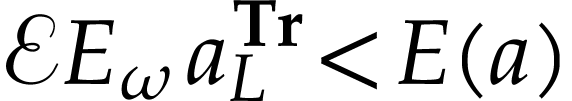 ,
and likewise
,
and likewise 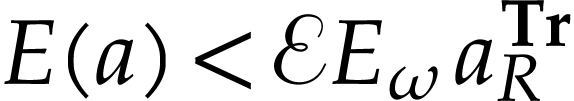 . We have
. We have 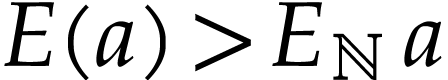 by
by 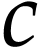 ) so
) so
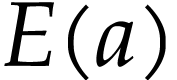 lies in the cut
lies in the cut
Recall that  holds by definition, so
holds by definition, so  .
.
Acknowledgments. The first author is supported by the French Belgian Community through a F.R.I.A. grant. The third author is supported by EPSRC (grant reference EP/T018461/1).
M. Aschenbrenner, L. van den Dries, and J. van der Hoeven. Asymptotic Differential Algebra and Model Theory of Transseries. Number 195 in Annals of Mathematics studies. Princeton University Press, 2017.
M. Aschenbrenner, L. van den Dries, and J. van der Hoeven. On numbers, germs, and transseries. In Proc. Int. Cong. of Math. 2018, volume 1, pages 1–24. Rio de Janeiro, 2018.
V. Bagayoko and J. van der Hoeven. Surreal substructures. HAL-02151377 (pre-print), 2019.
A. Berarducci and V. Mantova. Surreal numbers, derivations and transseries. JEMS, 20(2):339–390, 2018.
A. Berarducci and V. Mantova. Transseries as germs of surreal functions. Trans. of the AMS, 371:3549–3592, 2019.
M. Boshernitzan. Hardy fields and existence of transexponential functions. Aequationes mathematicae, 30:258–280, 1986.
L. van den Dries and Ph. Ehrlich. Fields of surreal numbers and exponentiation. Fundamenta Mathematicae, 167(2):173–188, 2001.
L. van den Dries, J. van der Hoeven, and E. Kaplan. Logarithmic hyperseries. Trans. of the AMS, 372(7):5199–5241, 2019.
J. Écalle. Introduction aux fonctions analysables et preuve constructive de la conjecture de Dulac. Hermann, collection: Actualités mathématiques, 1992.
H. Gonshor. An Introduction to the Theory of Surreal Numbers. Cambridge Univ. Press, 1986.
J. van der Hoeven. Automatic asymptotics. PhD thesis, École polytechnique, Palaiseau, France, 1997.
J. van der Hoeven. Operators on generalized power series. Journal of the Univ. of Illinois, 45(4):1161–1190, 2001.
J. van der Hoeven. Transseries and real differential algebra, volume 1888 of Lecture Notes in Mathematics. Springer-Verlag, 2006.
H. Kneser. Reelle analytische lösung der
gleichung 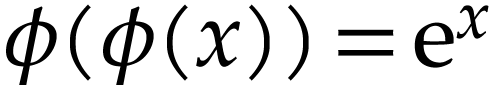 und verwandter
funktionalgleichungen. Journal Für Die Reine Und
Angewandte Mathematik, 1950:56–67, 01 1950.
und verwandter
funktionalgleichungen. Journal Für Die Reine Und
Angewandte Mathematik, 1950:56–67, 01 1950.
S. Kuhlmann and M. Matusinski. The exponential-logarithmic equivalence classes of surreal numbers. Order 32, pages 53–68, 2015.
B. H. Neumann. On ordered division rings. Trans. A.M.S., 66:202–252, 1949.
M. C. Schmeling. Corps de transséries. PhD thesis, Université Paris-VII, 2001.