In my thesis, I have shown how to represent surreal numbers, as defined
by Conway [6], as hyperseries, which
are generalizations of Dahn-Göring
[7] and Écalle's [8]
transseries.
Hyperseries are generalized power series 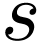 in a
variable
in a
variable 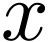 , which are endowed
with a hyperserial structure: a collection of functions
, which are endowed
with a hyperserial structure: a collection of functions
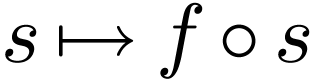 which are regular (e.g. analytic and monotone)
in a formal sense, and which are themselves represented as hyperseries
which are regular (e.g. analytic and monotone)
in a formal sense, and which are themselves represented as hyperseries
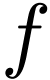 . These functions include
. These functions include
-
exponentials 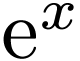 and logarithms
and logarithms 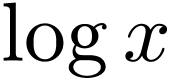 ,
,
-
so-called hyperexponentials, e.g. a formal term
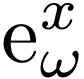 which satisfies Abel's equation
which satisfies Abel's equation
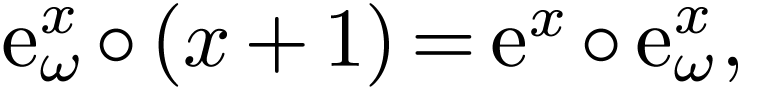
and its functional inverse 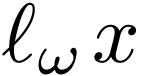 with
with 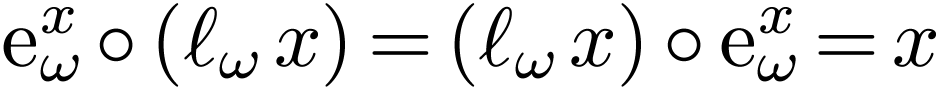 ,
,
-
so-called nested series such as expansions with
transfinite depth
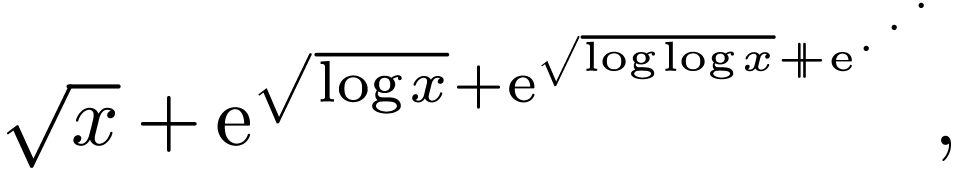 |
(1) |
which can be made rigorous sense of in hyperseries.
My thesis consisted in showing that the class  of
surreal numbers has a natural hyperserial structure. This raised several
research questions that I am now interested in, and which I summarize
below.
of
surreal numbers has a natural hyperserial structure. This raised several
research questions that I am now interested in, and which I summarize
below.
1Defining the derivation and composition law
on 
Using the hyperserial structure on the non-Archimedean ordered field
extension 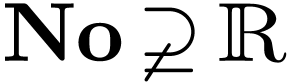 , it is possible to
represent surreal numbers as hypereries with real coefficients. This
representation gives a natural way to treat numbers as
functions defined on
, it is possible to
represent surreal numbers as hypereries with real coefficients. This
representation gives a natural way to treat numbers as
functions defined on 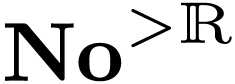 ,
and to differentiate them as such. In other words, this gives a
canonical way to define a derivation
,
and to differentiate them as such. In other words, this gives a
canonical way to define a derivation 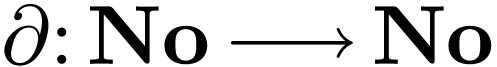 and a
composition law
and a
composition law 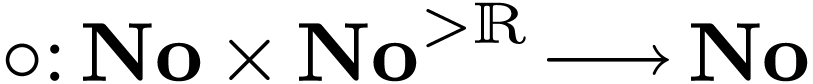 on surreal numbers. I have notes
on how to define these operations, that I plan to turn into a series of
papers.
on surreal numbers. I have notes
on how to define these operations, that I plan to turn into a series of
papers.
2Model theory of ordered structures with
composition
I want to study several problems related to the first-order structure
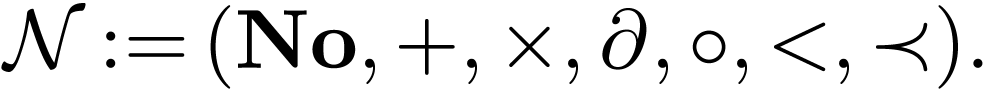
This structure has interesting properties: closure under conjugacy
equations, model completeness as an ordered valued differential field,
set-wise order saturation...
Nevertheless, it is difficult to even start studying its first-order
properties when taking the composition law into account, because not
much is known about the model theory of ordered structures with
(non-commutative) composition laws. I plan to propose interesting
first-order theories accounting for such structures, and to make baby
steps toward understanding  ,
which I believe is a prime and natural example of those.
,
which I believe is a prime and natural example of those.
2.1Growth order groups
One way to start is restrain ourselves to studying a small part of the
language which includes the composition law. Accordingly, the natural
candidate is the bi-ordered group  .
This group shares many first-order properties with ordered groups of
germs (at
.
This group shares many first-order properties with ordered groups of
germs (at 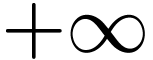 ) of definable
unary functions in o-minimal expansions of real-closed fields.
) of definable
unary functions in o-minimal expansions of real-closed fields.
I want to draw on this connection to further the knowledge about these
groups, as well as more abstract ordered groups which I call
growth order groups. The elementary class of growth
order groups in the language 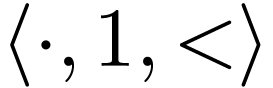 of ordered groups
is, roughly speaking, characterized by way the inequality
of ordered groups
is, roughly speaking, characterized by way the inequality
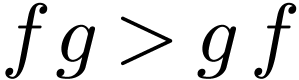
is solved in such groups. I studied in detail [3] a
prominent example of growth order group, which is a small subgroup of
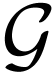 .
.
I expect that o-minimality is a natural source of growth ordered groups.
In particular, I want to prove or disprove the following conjecture:
Conjecture 2.1. Let
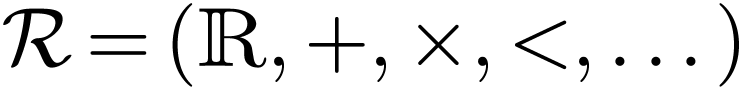 be an o-minimal expansion of the real ordered
field. Let
be an o-minimal expansion of the real ordered
field. Let 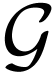 denote the group of germs at
denote the group of germs at 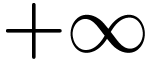 of
of 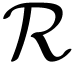 -definable
functions
-definable
functions  which tend to
which tend to 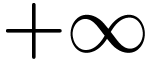 at
at 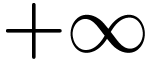 , ordered by comparison of
germs at
, ordered by comparison of
germs at 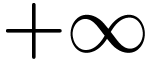 . Then
. Then  is a growth order group.
is a growth order group.
I can prove this in the particular case when the expansion of 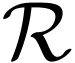 with the exponential function is levelled in the sense of
[12], and I would like to generalize this.
with the exponential function is levelled in the sense of
[12], and I would like to generalize this.
I expect that the non-commutative valuation theory of a growth orderd
group retains certain features of the valuation theory of Abelian
ordered groups. Just as valuation theory gives tools to obtain
asymptotic expansions of regular growth rates of an additive nature, I
expect that growth rates of functions definable in certain o-minimal
structures can be decomposed as non-commutative compositions of simpler
growth rates. Growth order groups are a way to make this idea precise.
Another way is to find a formal framework in which transfinite
non-commutative product make sense and can be made to form a growth
order group. I have an ongoing project of defining such structures, and
showing that certain groups of positive infinite transseries are of this
form.
2.2Model theoretic approach to recursive
definitions
A crucial feature of surreal numbers is the possibility of defining
operations on Cartesian powers of  via
recursive definitions as per [9]. Indeed
this is how the arithmetic [6] and exponential function [10] and hyperserial structure [4] on
via
recursive definitions as per [9]. Indeed
this is how the arithmetic [6] and exponential function [10] and hyperserial structure [4] on  were defined. It is sometimes possible [9] to
show that a function with recursive definition on
were defined. It is sometimes possible [9] to
show that a function with recursive definition on  is “tame”, for instance satisfying the intermediate
value property (IVT). This is particularly interesting because
having the IVT for unary terms in a first-order language is sometimes
conducive to proving existential closedness for the corresponding
structure (e.g. adding the IVT for terms to linearly ordered Abelian
groups, ordered domains, and Liouville-closed H-fields with small
derivation gives existential closedness).
is “tame”, for instance satisfying the intermediate
value property (IVT). This is particularly interesting because
having the IVT for unary terms in a first-order language is sometimes
conducive to proving existential closedness for the corresponding
structure (e.g. adding the IVT for terms to linearly ordered Abelian
groups, ordered domains, and Liouville-closed H-fields with small
derivation gives existential closedness).
Thus it would be interesting to generalize previous constructions of
opertions on  with a more model theoretic
approach. In particular given a first-order language
with a more model theoretic
approach. In particular given a first-order language 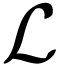 with
with 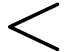 as the only relation symbol, and an
as the only relation symbol, and an 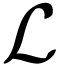 -theory
-theory 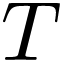 of
dense linear orders without endpoints, when and how (and in what order)
can one define, in a recursive way, interpretations of the function
symbols
of
dense linear orders without endpoints, when and how (and in what order)
can one define, in a recursive way, interpretations of the function
symbols 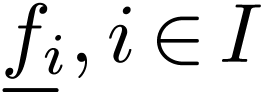 in
in 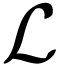 as functions
as functions
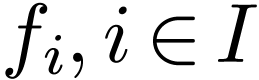 on
on  and its Cartesian
powers, in such a way that
and its Cartesian
powers, in such a way that 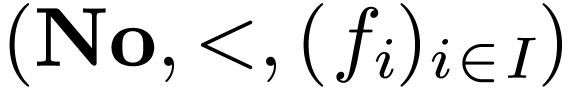 be a model of
be a model of 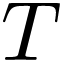 ? When doing so, what is the
complete theory
? When doing so, what is the
complete theory 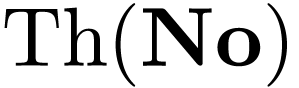 which we obtain?
which we obtain?
3Hyperexponential and nested functions
3.1Real hyperexponentiation
One long standing open question in o-minimality is the existence of a
transexponential o-minimal expansion of the real
ordered exponential field, i.e. an expansion which defines a unary
function growing faster than any finite iterate of 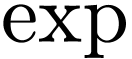 . Abel's equation in
. Abel's equation in 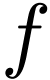
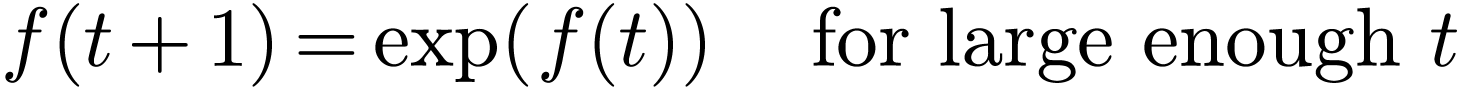 |
(3.1) |
is the simplest functional equation whose solutions in Hardy fields [5] are transexponential.
On the real-analytic side, Kneser's [11] solution 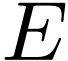 to (3.1) on
to (3.1) on 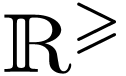 is a
natural candidate for such o-minimal investigations. On the
formal-surreal side, I hope that the calculus of hyperseries on
is a
natural candidate for such o-minimal investigations. On the
formal-surreal side, I hope that the calculus of hyperseries on  faithfully represents asymptotic properties (at
faithfully represents asymptotic properties (at 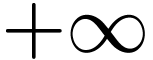 ) of
) of 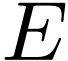 .
Recently, Adele Padgett studied in
her PhD thesis [13] a first-order theory
.
Recently, Adele Padgett studied in
her PhD thesis [13] a first-order theory 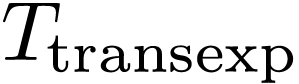 for
for 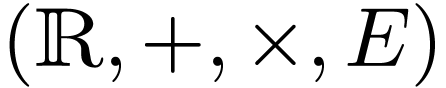 in an expanded language
in an expanded language 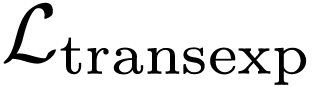 , and showed that the the field
, and showed that the the field 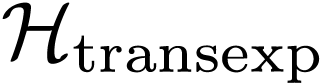 of germs of unary terms in
of germs of unary terms in 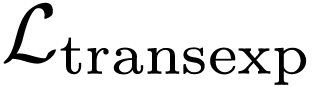 is a
Hardy field. Surreal numbers with the natural hyperexponential form a
natural model of
is a
Hardy field. Surreal numbers with the natural hyperexponential form a
natural model of 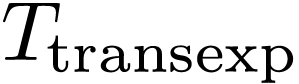 . A first
step towards studying the relationship between the surreal/formal model
. A first
step towards studying the relationship between the surreal/formal model
 and the geometric/analytic model
and the geometric/analytic model 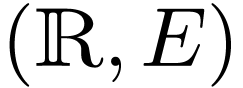 is to prove that there is a natural inclusion
is to prove that there is a natural inclusion
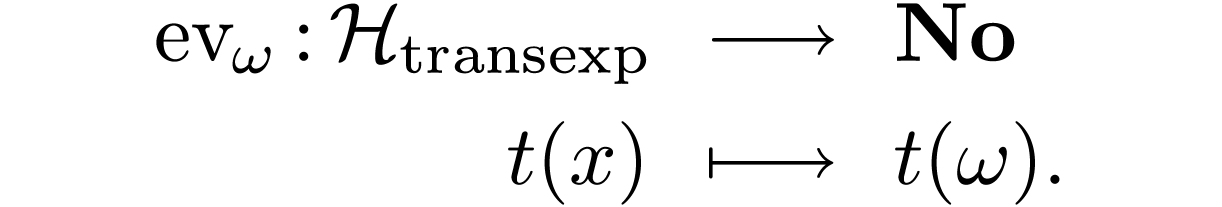
Together with A. Padgett and E. Kaplan,
we have started to work on the following conjectures:
Conjecture 3.1. The function
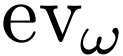 is a well-defined
is a well-defined 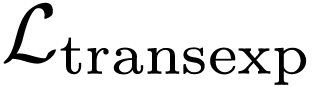 -embedding.
-embedding.
Conjecture 3.2. The
function 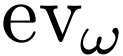 commutes with the derivations and
composition laws on
commutes with the derivations and
composition laws on 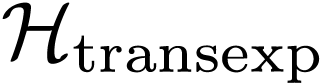 and
and  .
.
3.2Nested germs
A unique feature of surreal numbers is that they naturally contain
nested numbers, e.g. numbers which expand as
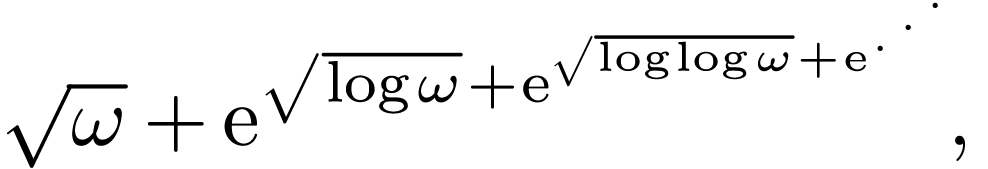 |
(3.2) |
where 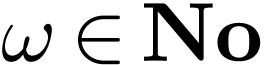 is a specific surreal number which plays
the role of a positive infinite variable.
is a specific surreal number which plays
the role of a positive infinite variable.
On the geometric/analytic side, the functional equation
 |
(3.3) |
naturally generate germs which, when represented using
logarithmico-exponential terms, expand in a similar way as (3.2).
There are good reasons [2] to believe that the behavior of
differential polynomials on these “nested germs” is exactly
the same as their behavior on the corresponding nested numbers.
Exploiting this, I want to study how the functional equation (3.2)
can be solved in Hardy fields:
Question. What linear orderings can be represented by
the set of quasi-analytic solutions of (3.3) lying in a
common Hardy field?
Bibliography
-
[1]
-
M. Aschenbrenner, L. van den Dries, and J. van der
Hoeven. Asymptotic Differential Algebra and Model Theory of
Transseries. Number 195 in Annals of Mathematics studies.
Princeton University Press, 2017.
-
[2]
-
M. Aschenbrenner, L. van den Dries, and J. van der
Hoeven. Filling gaps in Hardy fields. Technical Report,
Gödel Institute, UIUC, C.N.R.S., 2022.
-
[3]
-
V. Bagayoko. Hyperexponentially closed fields.
Technical Report, UMons, LIX, 2022.
-
[4]
-
V. Bagayoko and J. van der Hoeven. The hyperserial
field of surreal numbers. Technical Report, UMons, LIX,
C.N.R.S., 2021. HAL-03232836.
-
[5]
-
M. Boshernitzan. Hardy fields and existence of
transexponential functions. Aequationes mathematicae,
30:258–280, 1986.
-
[6]
-
J. H. Conway. On numbers and games. Academic
Press, 1976.
-
[7]
-
B. Dahn and P. Göring. Notes on
exponential-logarithmic terms. Fundamenta Mathematicae,
127(1):45–50, 1987.
-
[8]
-
J. Écalle. Introduction aux fonctions
analysables et preuve constructive de la conjecture de
Dulac. Actualités Mathématiques. Hermann,
1992.
-
[9]
-
A. Fornasiero. Recursive definitions on surreal
numbers. ArXiv:math/0612234v1, 2018.
-
[10]
-
H. Gonshor. An Introduction to the Theory of
Surreal Numbers. Cambridge Univ. Press, 1986.
-
[11]
-
H. Kneser. Reelle analytische Lösung der
Gleichung 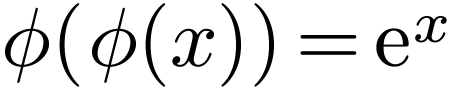 und erwandter
Funktionalgleichungen. Journal Für Die Reine Und
Angewandte Mathematik, 1950:56–67, 01 1950.
und erwandter
Funktionalgleichungen. Journal Für Die Reine Und
Angewandte Mathematik, 1950:56–67, 01 1950.
-
[12]
-
D. Marker and C. Miller. Levelled o-minimal
structures. Revista Matematica de la Universidad Complutense
de Madrid, 10, 1997.
-
[13]
-
A. Padgett. Sublogarithmic-transexponential
series. PhD thesis, Berkeley, 2022.
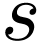 in a
variable
in a
variable 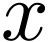 , which are endowed
with a hyperserial structure: a collection of functions
, which are endowed
with a hyperserial structure: a collection of functions
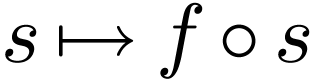 which are regular (e.g. analytic and monotone)
in a formal sense, and which are themselves represented as hyperseries
which are regular (e.g. analytic and monotone)
in a formal sense, and which are themselves represented as hyperseries
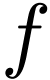 . These functions include
. These functions include
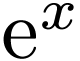 and logarithms
and logarithms 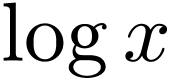 ,
,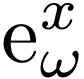 which satisfies Abel's equation
which satisfies Abel's equation
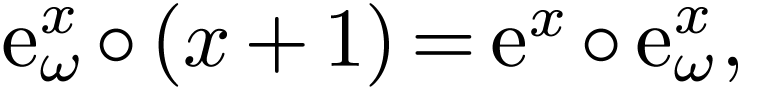
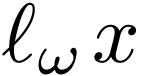 with
with 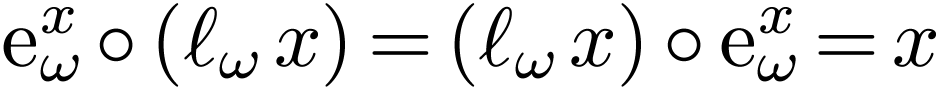 ,
,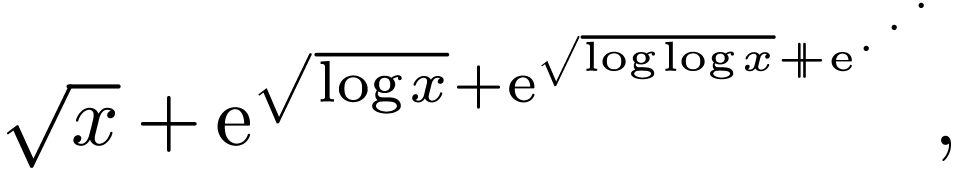
 of
surreal numbers has a natural hyperserial structure. This raised several
research questions that I am now interested in, and which I summarize
below.
of
surreal numbers has a natural hyperserial structure. This raised several
research questions that I am now interested in, and which I summarize
below.
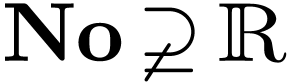 ,
,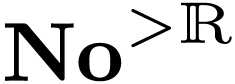 ,
,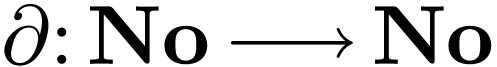 and a
composition law
and a
composition law 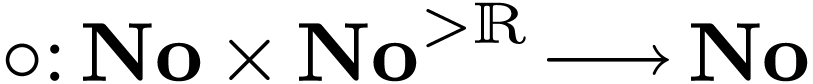 on surreal numbers. I have notes
on how to define these operations, that I plan to turn into a series of
papers.
on surreal numbers. I have notes
on how to define these operations, that I plan to turn into a series of
papers.
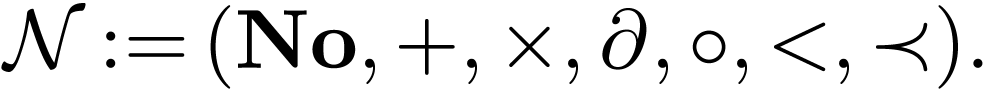
 ,
, .
.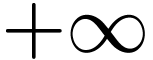 )
)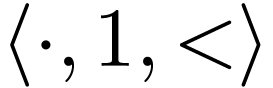 of ordered groups
is, roughly speaking, characterized by way the inequality
of ordered groups
is, roughly speaking, characterized by way the inequality
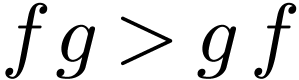
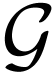 .
.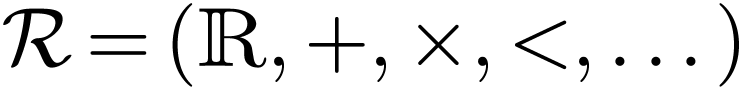 be an o-minimal expansion of the real ordered
field. Let
be an o-minimal expansion of the real ordered
field. Let 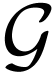 denote the group of germs at
denote the group of germs at 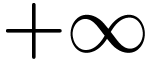 of
of 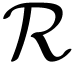 -definable
-definable which tend to
which tend to 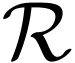 with the exponential function is levelled in the sense of
[
with the exponential function is levelled in the sense of
[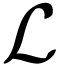 with
with 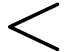 as the only relation symbol, and an
as the only relation symbol, and an 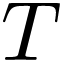 of
dense linear orders without endpoints, when and how (and in what order)
can one define, in a recursive way, interpretations of the function
symbols
of
dense linear orders without endpoints, when and how (and in what order)
can one define, in a recursive way, interpretations of the function
symbols 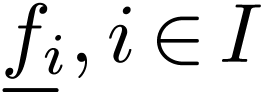 in
in 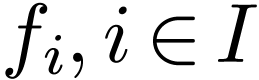 on
on 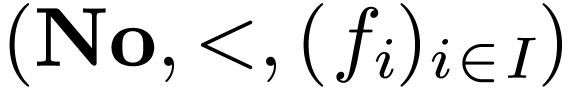 be a model of
be a model of 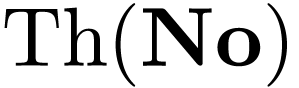 which we obtain?
which we obtain?
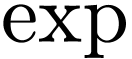 .
.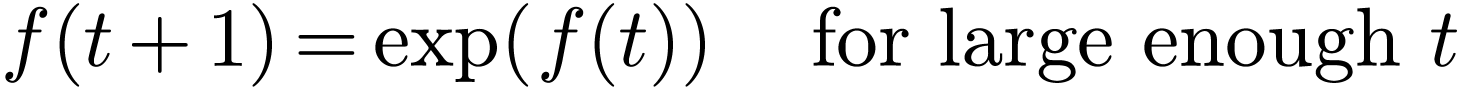
 to (
to (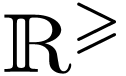 is a
natural candidate for such o-minimal investigations. On the
formal-surreal side, I hope that the calculus of hyperseries on
is a
natural candidate for such o-minimal investigations. On the
formal-surreal side, I hope that the calculus of hyperseries on 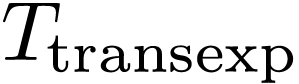 for
for 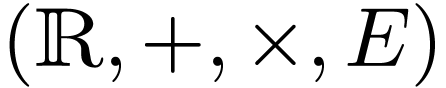 in an expanded language
in an expanded language 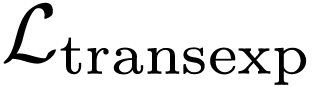 ,
,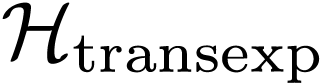 of germs of unary terms in
of germs of unary terms in 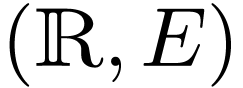 is to prove that there is a natural inclusion
is to prove that there is a natural inclusion
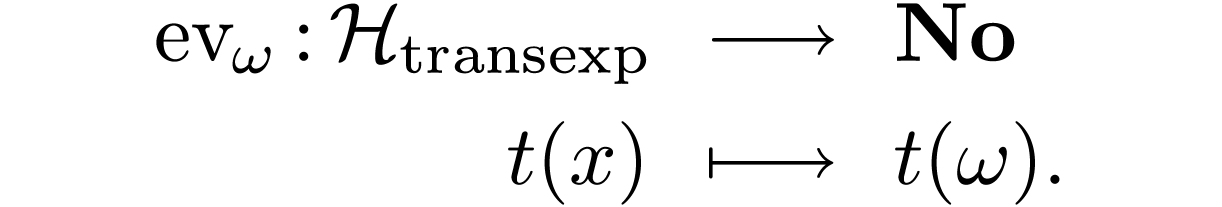
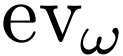 is a well-defined
is a well-defined  .
.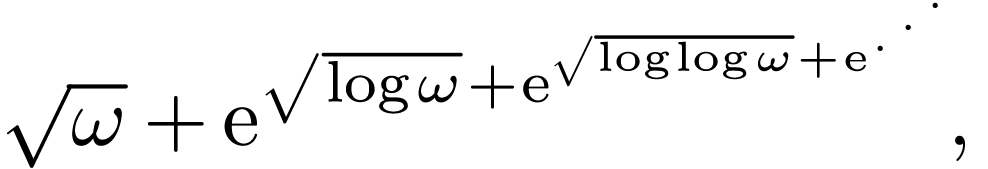
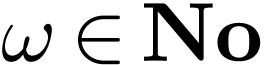 is a specific surreal number which plays
the role of a positive infinite variable.
is a specific surreal number which plays
the role of a positive infinite variable.

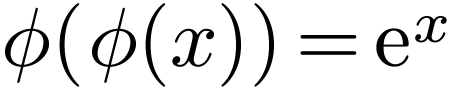 und erwandter
Funktionalgleichungen. Journal Für Die Reine Und
Angewandte Mathematik, 1950:56–67, 01 1950.
und erwandter
Funktionalgleichungen. Journal Für Die Reine Und
Angewandte Mathematik, 1950:56–67, 01 1950.