In my PhD thesis [5], I have shown how to represent Conway's surreal numbers [16] as
hyperseries, which are generalisations of Dahn-Göring [17] and Écalle's
transseries. Hyperseries are generalised power series 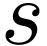 in a variable
in a variable 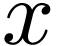 , that are
endowed with a hyperserial structure [13]:
a collection of functions
, that are
endowed with a hyperserial structure [13]:
a collection of functions 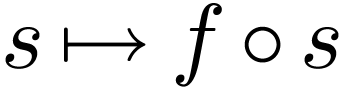 that are regular (e.g.
analytic and monotone) in a formal sense, and which are themselves
represented as hyperseries
that are regular (e.g.
analytic and monotone) in a formal sense, and which are themselves
represented as hyperseries 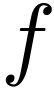 .
These functions include:
.
These functions include:
-
exponentials 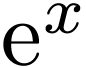 and logarithms
and logarithms 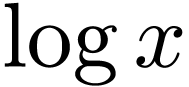 ,
,
-
so-called hyperexponentials, e.g. a formal term
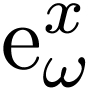 which satisfies Abel's equation
which satisfies Abel's equation
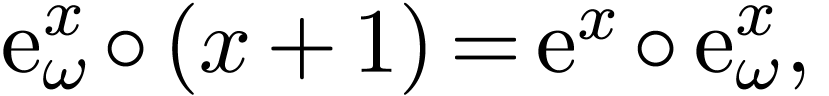
and its functional inverse 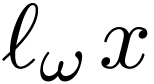 with
with 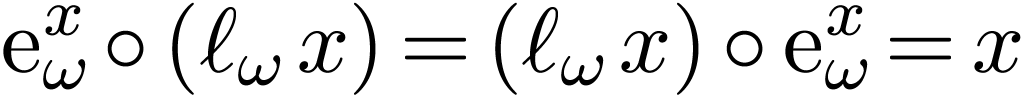 ,
,
-
so-called nested series such as expansions with
transfinite depth
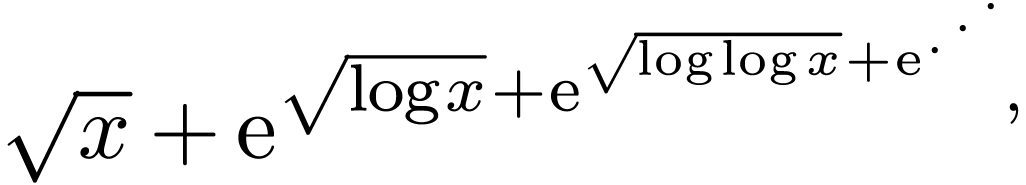 |
(1) |
which in can be made rigorous sense of in hyperseries.
My thesis consisted in showing that the class  of
surreal numbers has a natural hyperserial structure. This has sprouted a
series of research questions that are summarized below.
of
surreal numbers has a natural hyperserial structure. This has sprouted a
series of research questions that are summarized below.
1Defining the derivation and composition
law
Using the hyperserial structure on the non-Archimedean ordered field
 of surreal numbers [11], it is
possible to represent surreal numbers as hperseries with real
coefficients [12]. This representation gives a natural way
to treat numbers as functions defined on the class
of surreal numbers [11], it is
possible to represent surreal numbers as hperseries with real
coefficients [12]. This representation gives a natural way
to treat numbers as functions defined on the class 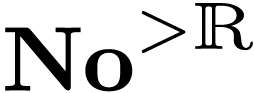 of positive infinite numbers, and to
differentiate them as such. In other words, this gives a
canonical way to define a composition law
of positive infinite numbers, and to
differentiate them as such. In other words, this gives a
canonical way to define a composition law 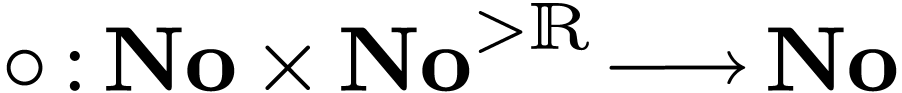 and a
derivation
and a
derivation 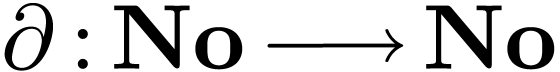 on surreal numbers. This is van der
Hoeven's conjecture:
on surreal numbers. This is van der
Hoeven's conjecture:
Conjecture A. [22] There is
are a derivation and a composition law on  that
are compatible with its hyperserial structure.
that
are compatible with its hyperserial structure.
I have notes which define these operations and derive their main
elementary properties. I plan to turn them into a series of papers,
partly in joint work with J. van der Hoeven. This
series recently started by a technical note [9], in which I
showed how to compose numbers by monomials that are “sufficiently
hyperexponential”.
2Model theory of groups of regular growth
rates
I am studying several inter-related problems motivated by the
investigation of the first-order structure
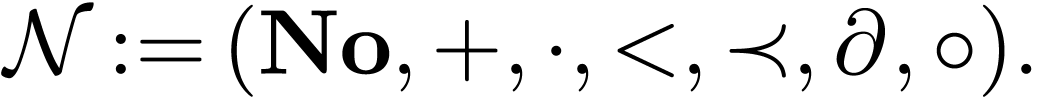
This structure has interesting properties: closedness under conjugacy
equations, model completeness as an ordered valued differential field
[1, 2], set-wise order saturation...
Unfortunately, it is difficult to even start looking into its
first-order properties when taking the composition law into account,
because little is known about first-order theories of ordered structures
with composition laws. My long-term plan is to build toward an
understanding of some of these structures, in the hope of establishing
tameness properties of  and other such
structures.
and other such
structures.
2.1Growth order groups
One way to begin this journey is to restrain oneself to a small reduct
of  . The natural candidate is
the ordered group
. The natural candidate is
the ordered group 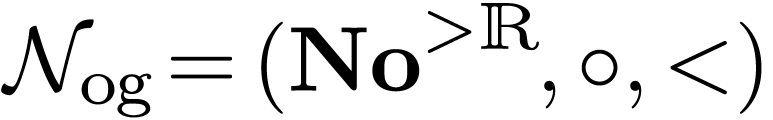 . It shares
many first-order properties with ordered groups of germs at
. It shares
many first-order properties with ordered groups of germs at 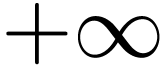 of definable unary functions in o-minimal expansions of
real-closed fields. Drawing on this connection, I introduced [10]
an elementary class of ordered groups, called growth order
groups (henceforth GOGs), that is intended to subsume the
informal notion of group of regular growth rates, exemplified both by
o-minimal germs and hyperseries. I expect that o-minimality is a natural
source of GOGs. In particular, I want to prove the following:
of definable unary functions in o-minimal expansions of
real-closed fields. Drawing on this connection, I introduced [10]
an elementary class of ordered groups, called growth order
groups (henceforth GOGs), that is intended to subsume the
informal notion of group of regular growth rates, exemplified both by
o-minimal germs and hyperseries. I expect that o-minimality is a natural
source of GOGs. In particular, I want to prove the following:
Conjecture B. Let 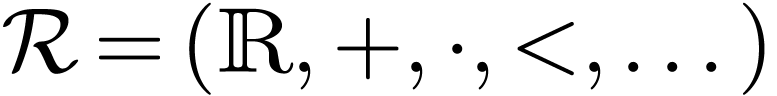 be an
o-minimal expansion of the real ordered field. The ordered group, under
composition and comparison at infinity, of germs at
be an
o-minimal expansion of the real ordered field. The ordered group, under
composition and comparison at infinity, of germs at 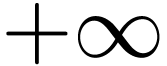 of unary
of unary 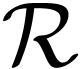 -definable maps
-definable maps  is a growth order group.
is a growth order group.
The special case when 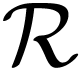 is levelled in the sense
of [27] was proved in [10].
is levelled in the sense
of [27] was proved in [10].
2.2Equations over valued
groups
Growth order groups come equipped with a canonical definable valuation,
which plays a prominent role in establishing their properties. An
important matter to be understood regarding GOGs is the unary equation
problem: given a GOG 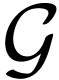 and a unary term
and a unary term 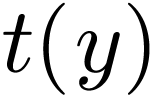 in the language of groups with parameters in
in the language of groups with parameters in 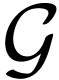 , when is there a growth order group
, when is there a growth order group 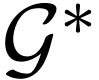 extending
extending 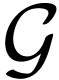 such that
such that
 |
(2.1) |
Indeed, this question is a baby version of the search for existentially
closed GOGs. Seeing 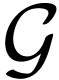 as a group of o-minimal
germs, or formal series under composition, the equation
as a group of o-minimal
germs, or formal series under composition, the equation 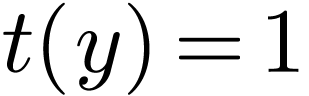 translates to an intricate functional equation
translates to an intricate functional equation
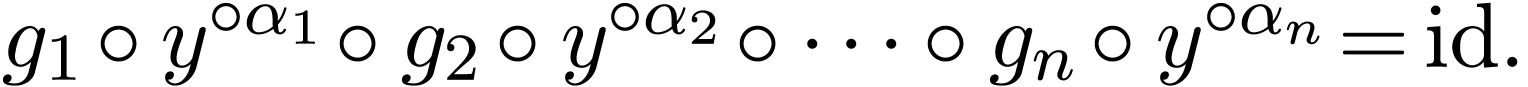
No practical theory of such general fuctional equations exists.
Ordered groups of o-minimal germs for expansions
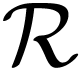 of general real-closed fields may fail to be GOGs. Likewise, basic
expansions of a GOG related to the unary equation problem fail to be
GOGs. This calls for an extension of the class of growth ordered groups
to a larger class of
valued groups
that would encompass all the groups involved in the unary equation
problem for GOGs, while retaining sufficiently many properties of the
canonical valuation on GOGs that equations over these valued groups be
traceable. We introduced [
6
] these valued groups, called c-valued groups, and studied their
properties.
Nearly Abelian
c-valued groups are c-valued groups in which commutators decrease in
valuation. They include for instance groups of parabolic
of general real-closed fields may fail to be GOGs. Likewise, basic
expansions of a GOG related to the unary equation problem fail to be
GOGs. This calls for an extension of the class of growth ordered groups
to a larger class of
valued groups
that would encompass all the groups involved in the unary equation
problem for GOGs, while retaining sufficiently many properties of the
canonical valuation on GOGs that equations over these valued groups be
traceable. We introduced [
6
] these valued groups, called c-valued groups, and studied their
properties.
Nearly Abelian
c-valued groups are c-valued groups in which commutators decrease in
valuation. They include for instance groups of parabolic
2.1
formal series, or GOGs of parabolic o-minimal germs. Our theory is
suited to studying unary equations over certain pure groups as well as
exponential groups in the sense of [
28
,
29
]. Adapting some classical valuation theoretic notions, such as residues
and spherical completeness, to the case of non-Abelian groups (see also
[
31
]), we obtained in particular:
Theorem 2.1. [6,
Theorem 2] Let 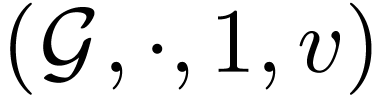 be a spherically complete,
torsion-free, nearly Abelian c-valued group. Suppose that its (Abelian)
residue groups are divisible. Then any equation
be a spherically complete,
torsion-free, nearly Abelian c-valued group. Suppose that its (Abelian)
residue groups are divisible. Then any equation
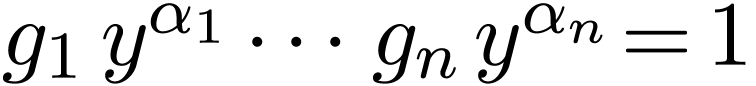
where 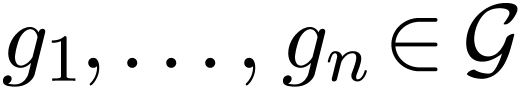 and
and 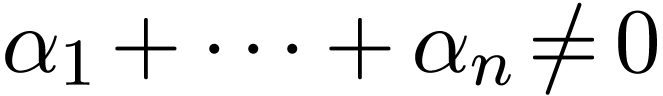 has a
unique solution
has a
unique solution 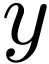 in
in 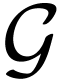 .
.
To us, this would give a satisfactory partial answer to the unary
equation problem restricted to non-singular equations, i.e. equations
with 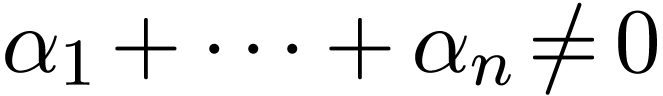 , if we had a
positive answer to the following question:
, if we had a
positive answer to the following question:
Question C. Given a c-valued group 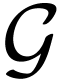 , is there a spherically complete c-valued
group
, is there a spherically complete c-valued
group 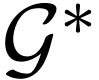 extending
extending 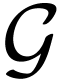 ?
?
Our next goal besides answering that question is to find valued groups
in which the geometry of definable sets is tame (see Section 3.4).
This mainly entails solving singular equations over valued groups. We
have a candidate of a good first-order theory whose models have this
feature.
2.3Model theoretic approach to recursive
surreal definitions
A defining aspect of  is the possibility of
defining operations on its Cartesian powers via
recursive definitions as per [19]. Indeed
this is how the arithmetic [16], exponential function [20] and hyperserial structure [11] were defined.
It is sometimes possible [19] to show that a function with
a recursive definition on
is the possibility of
defining operations on its Cartesian powers via
recursive definitions as per [19]. Indeed
this is how the arithmetic [16], exponential function [20] and hyperserial structure [11] were defined.
It is sometimes possible [19] to show that a function with
a recursive definition on  is “tame”,
for instance satisfying the intermediate value property (IVP). This is
particularly interesting because the IVP for unary terms in a
first-order language is sometimes sufficient to entail existential
closedness forthe corresponding structure (e.g. adding the IVP axiom
scheme for unary terms to the theories of linearly ordered Abelian
groups, ordered domains, or Liouville-closed H-fields with small
derivation [1] yields their model companion).
is “tame”,
for instance satisfying the intermediate value property (IVP). This is
particularly interesting because the IVP for unary terms in a
first-order language is sometimes sufficient to entail existential
closedness forthe corresponding structure (e.g. adding the IVP axiom
scheme for unary terms to the theories of linearly ordered Abelian
groups, ordered domains, or Liouville-closed H-fields with small
derivation [1] yields their model companion).
Thus it would be interesting to revisit and generalise previous
definitions of operations on  with a more model
theoretic approach. In particular, given a first-order language
with a more model
theoretic approach. In particular, given a first-order language 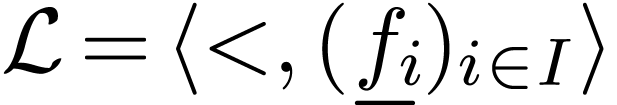 where each
where each 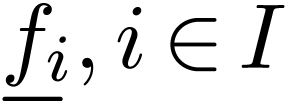 is a function
symbol, and an
is a function
symbol, and an  -theory
-theory 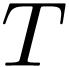 of dense linear orders without endpoints, whn and how
(and in what order) can one recursively define interpretations of the
function symbols
of dense linear orders without endpoints, whn and how
(and in what order) can one recursively define interpretations of the
function symbols 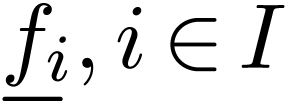 as function
as function 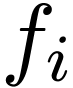 on Cartesian powers of
on Cartesian powers of  , in
such a way that
, in
such a way that 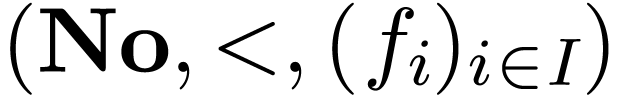 be a model of
be a model of 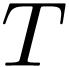 ? When doing so, what is the complete theory
? When doing so, what is the complete theory
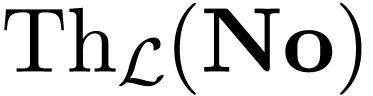 of
of  ?
?
3Lie calculus for algebras and groups of
formal series
The formal realm usually serves as a collection of convenient extensions
of first-order structures in which many equations or existential
formulas are satisfied. Developping formal versions of classical tools
in algebra, geometry and analysis is a way to build formal structures
fitting our goals, for instance satisfying a given first-order theory.
3.1Formal Lie correspondence
Together with S. L. Krapp, S. Kuhlmann,
D. C. Panazzolo and M. Serra,
we showed [14] that a fraction of the classical Lie theory
applies to Lie algebras of generalised formal series called Noetherian
series (see [21]). They come equipped with a partial
ordering  of strict dominance, and a notion of
infinite sums, for which linear maps commuting with infinite sums are
said strongly linear. They include for instance algebras of
formal power series in commuting or non-commuting variables, and Hahn
series fields and skew-fields. We showed:
of strict dominance, and a notion of
infinite sums, for which linear maps commuting with infinite sums are
said strongly linear. They include for instance algebras of
formal power series in commuting or non-commuting variables, and Hahn
series fields and skew-fields. We showed:
Theorem 3.1. Let 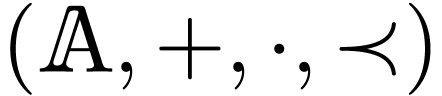 be an algebra, in characteristic
be an algebra, in characteristic 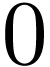 , of Noetherian series. Then the formal Taylor
series of the exponential map induces an isomorphism between the group
, of Noetherian series. Then the formal Taylor
series of the exponential map induces an isomorphism between the group
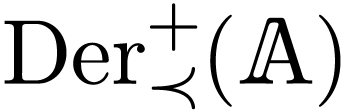 of strongly linear derivations
of strongly linear derivations 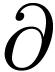 on
on  with
with 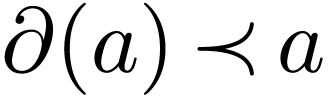 for all
for all 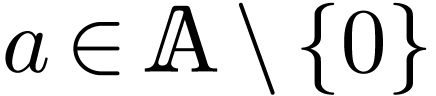 and the group
and the group 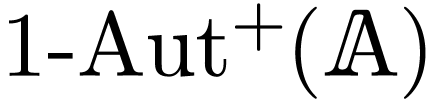 under
composition of strongly linear automorphisms
under
composition of strongly linear automorphisms  of
of
 with
with 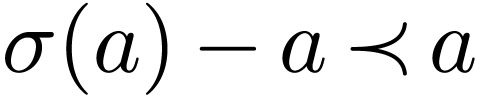 for all
for all 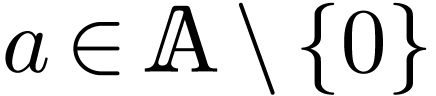 .
.
The group law on 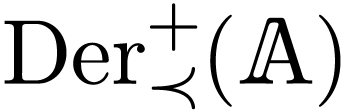 is given by a formal
Baker-Campbell-Hausdorff product (see [32]). There is also
a formal verison of the third homomorphism theorem. We call these
relations the formal Lie correspondence. Motivated by
[26], this raises the question:
is given by a formal
Baker-Campbell-Hausdorff product (see [32]). There is also
a formal verison of the third homomorphism theorem. We call these
relations the formal Lie correspondence. Motivated by
[26], this raises the question:
Question D. Does the formal Lie correspondence extend
between a Lie subalgebra of the algebra 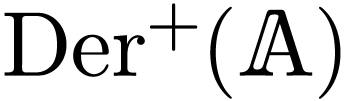 of
strongly linear derivations on
of
strongly linear derivations on  and the group
and the group
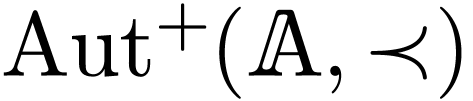 of strongly linear automorphism of
of strongly linear automorphism of 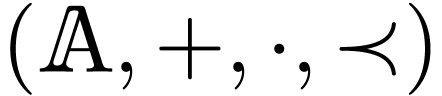 ?
?
3.2Groups with linearly ordered infinite
products
In analogy with valuation theory in commutative algebra (see e.g. [25] and [23]), we expect that elements 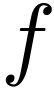 in sufficiently large groups of o-minimal germs should
have compositional asymptotic expansions
in sufficiently large groups of o-minimal germs should
have compositional asymptotic expansions
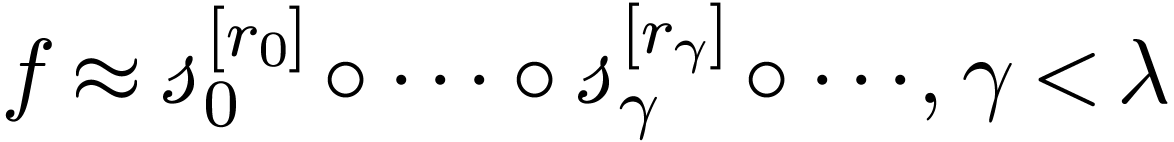
where 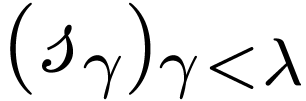 is a scale of functions that is strictly
decreasing in rate of growth,
is a scale of functions that is strictly
decreasing in rate of growth, 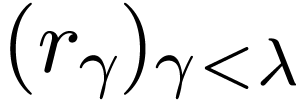 is a sequence of
non-zero real numbers, and
is a sequence of
non-zero real numbers, and 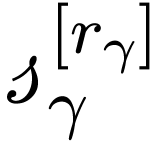 denotes the
denotes the 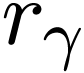 -th real iterate of
-th real iterate of 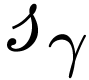 . The formalisation of such asymptotic
expansions was done in the general cases of growth order groups and
valued groups, in [10, 6], in the form of a
theory of scales and pseudo-Cauchy sequences. We lack a formalisation of
the expansions themselves that would be the non-commutative analogue of
fields of formal series, i.e. a group of formal non-commutative series
. The formalisation of such asymptotic
expansions was done in the general cases of growth order groups and
valued groups, in [10, 6], in the form of a
theory of scales and pseudo-Cauchy sequences. We lack a formalisation of
the expansions themselves that would be the non-commutative analogue of
fields of formal series, i.e. a group of formal non-commutative series
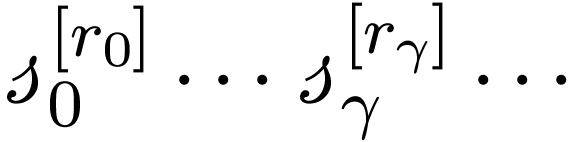 whose group operation depends only on the
assignment
whose group operation depends only on the
assignment 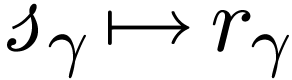 :
:
Question E. Given a linearly ordered set 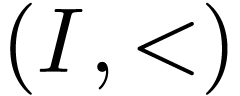 and a family
and a family 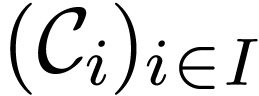 of Abelian ordered
groups, under what conditions can one define a group law
of Abelian ordered
groups, under what conditions can one define a group law  on the set
on the set 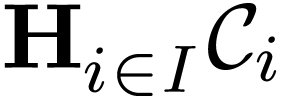 of functions
of functions 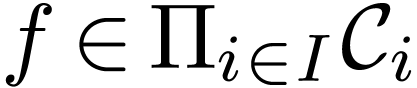 with anti-well-ordered support
with anti-well-ordered support 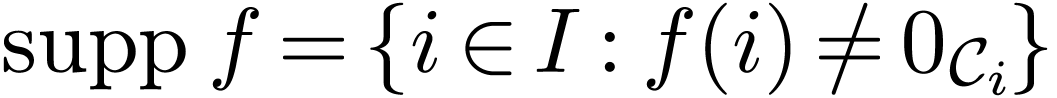 , ordered lexicographically, such that the ordered
group
, ordered lexicographically, such that the ordered
group 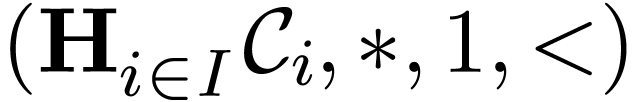 is a growth order group?
is a growth order group?
We proposed [8] a framework for studying infinite
linearly ordered products in general groups. We were able to
show that some classical groups of formal series can be endowed with
such infinite products in a canonical way, and showed that this gives a
canonical representation of their elements as formal non-commutative
series:
Theorem 3.2. (consequence
of [8, Theorems 4 and 5]) Let  be an ordered field, and let
be an ordered field, and let 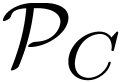 be the group under
composition of power series
be the group under
composition of power series 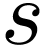 with
anti-well-ordered support, with exponents and coefficients in
with
anti-well-ordered support, with exponents and coefficients in  , that are tangent to the identity.
Then one can define transfinite linearly ordered products on
, that are tangent to the identity.
Then one can define transfinite linearly ordered products on 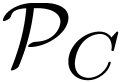 , and for each
, and for each 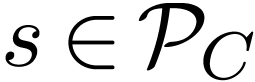 , there is a unique map
, there is a unique map 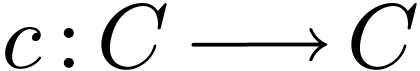 with anti-well-ordered support with
with anti-well-ordered support with 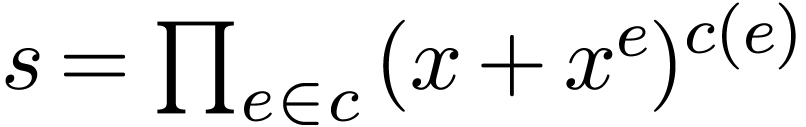 .
.
3.3Groups of formal series
In forthcoming work, relying on a study of Taylor expansions for
functions defined on fields of formal series in progress with V. L.
Mantova, we will show how to use infinite
compositions of formal series in order to study properties of sets of formal series with formal composition laws.
Work in progress. The set of positive infinite
finitely nested series of [4] is a group.
Moreover, any such series can be represented uniquely as a possibly
transfinite composition as in Theorem 3.2.
The same proof will apply to  provided the
composition law is defined.
provided the
composition law is defined.
3.4Conjugacy, resonance, and
asymptotic differential algebra
In order to investigate tame first-order theories of nearly Abelian
c-valued groups (see Section
2.2
), one needs to find such groups where definable sets are simple in a
geometric sense. A sound condition is that discreteness should only come
from Abelian subgroups (in GOGs, the
solutions 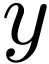 of
of 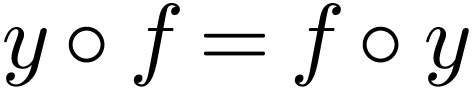 lie in a discrete Abelian subgroup, sometimes isomorphic to the group of integers, rational numbers or real numbers).
lie in a discrete Abelian subgroup, sometimes isomorphic to the group of integers, rational numbers or real numbers).
However, the phenomenon of Poincaré resonance
(see [18]) in normalisingng local objects such as germs of vector fields
and diffeomorphisms, precludes this. In the case of plain parabolic
formal power series 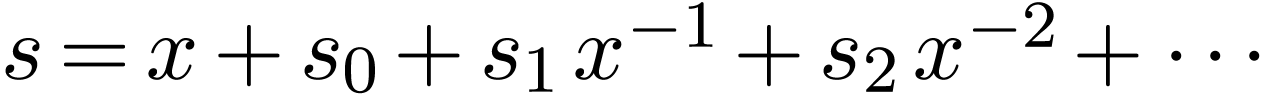 in
in 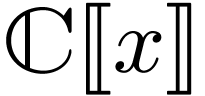 , we say that there is resonance when the the
shortest Laurent polynomial
, we say that there is resonance when the the
shortest Laurent polynomial 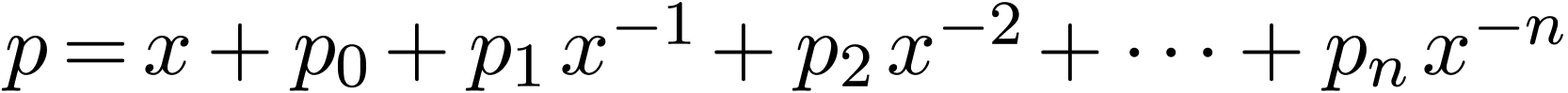 which is a conjugate
of
which is a conjugate
of 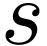 is not the truncation
is not the truncation 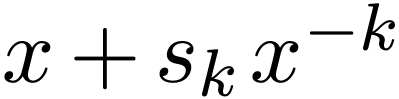 of
of 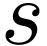 consisting in its first two non-zero terms,
but contains an additional resonant term
consisting in its first two non-zero terms,
but contains an additional resonant term 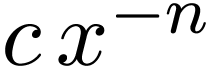 which depends on a longer truncation of
which depends on a longer truncation of 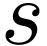 .
From a combinatorial standpoint, this means that the term
.
From a combinatorial standpoint, this means that the term 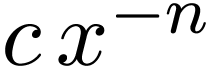 cannot be eliminated by elementary operations of
conjugation. From the standpoint of the model theory of valued groups,
this entails that the set of parabolic power series that are conjugates
of
cannot be eliminated by elementary operations of
conjugation. From the standpoint of the model theory of valued groups,
this entails that the set of parabolic power series that are conjugates
of 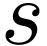 has infinitely many definable connected
components, which do not come from an Abelian subgroup.
has infinitely many definable connected
components, which do not come from an Abelian subgroup.
For us, this means that such groups as that of parabolic power series
are to be avoided. The reoccurrence of resonance was an unpleasant
hurdle in studying valued groups, until we found a way to interpret it
(in certain prominent cases) as a property of the underlying valued
differential fields of series. Working on the Lie algebra side of the
formal Lie correspondence, we were able [7] to formalise
resonance for certain groups of transseries and to establish an
equivalence between the non-existence of resonance and the existence of
asymptotic integrals (see [1, p 327]). Our equivalence was
only proved over certain fields of classical transseries. When the
composition law  and derivation
and derivation 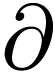 are defined on
are defined on  , we wish to
extend it thus:
, we wish to
extend it thus:
Conjecture F. Let 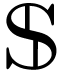 be a
direct limit of spherically complete differential subfields of
be a
direct limit of spherically complete differential subfields of 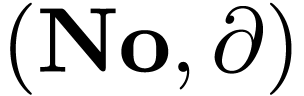 , and suppose that the set
, and suppose that the set  of parabolic elements in
of parabolic elements in 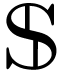 is a
nearly Abelian subgroup of the c-valued group of all parabolic numbers.
Then conjugacy in
is a
nearly Abelian subgroup of the c-valued group of all parabolic numbers.
Then conjugacy in  is resonance-free if and only
if
is resonance-free if and only
if 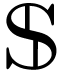 has asymptotic integration.
has asymptotic integration.
4Hyperexponential and nested functions
Lastly, we turn to more concrete and geometric questions regarding the
analytic content of the calculus of hyperseries.
4.1Real hyperexponentiation
One long-standing open problem in o-minimality is the existence of a
transexponential o-minimal expansion of the real
ordered exponential field, i.e. an expansion which defines a unary
function growing faster than all iterates of 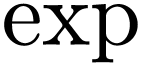 . Abel's equation in
. Abel's equation in 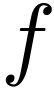
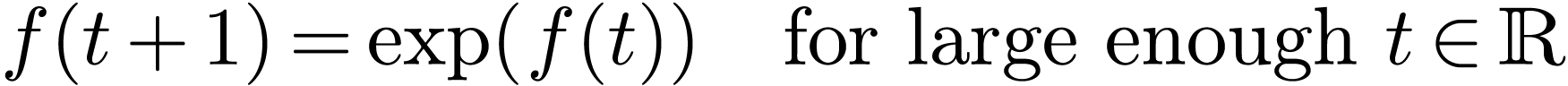 |
(4.1) |
is the simplest functional equation whose solutions [24] in
Hardy fields [15] are transexponential.
On the real-analytic side, Kneser's solution 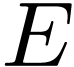 to
(4.1) on
to
(4.1) on 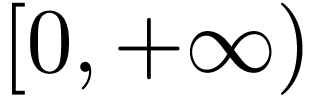 is a natural candidate for
these o-minimal investigations. On the formal-surreal side, I hope that
the calculus of hyperseries on
is a natural candidate for
these o-minimal investigations. On the formal-surreal side, I hope that
the calculus of hyperseries on  faithfully
represents asymptotic properties of
faithfully
represents asymptotic properties of 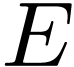 .
Recently, A. Padgett studied in her PhD thesis [30] a first-order theory
.
Recently, A. Padgett studied in her PhD thesis [30] a first-order theory 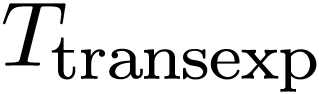 for
for 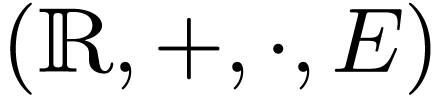 , in a language
, in a language 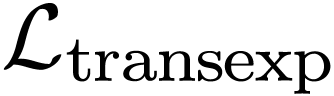 , and showed that the set
, and showed that the set 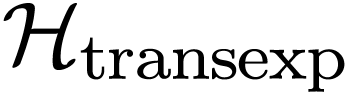 of germs of unary terms in
of germs of unary terms in 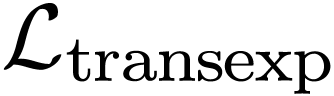 is a Hardy field. The
field
is a Hardy field. The
field 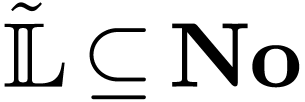 of finitely nested hyperseries [13],
with the hyperexponential function corresponding to
of finitely nested hyperseries [13],
with the hyperexponential function corresponding to 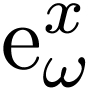 is a model of
is a model of 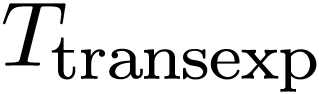 . A first step
toward studying the relationship between the surreal/formal model
. A first step
toward studying the relationship between the surreal/formal model 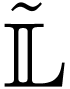 and the geometric/analytic model
and the geometric/analytic model 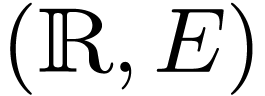 is to prove that there is a natural inclusion
is to prove that there is a natural inclusion
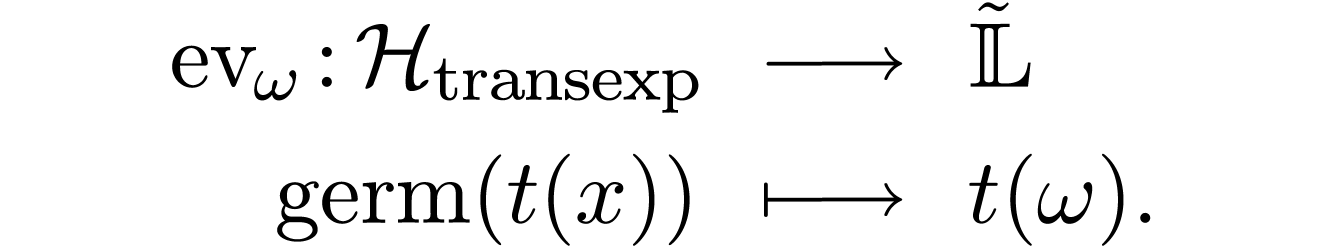
With A. Padgett and E. Kaplan,
we started working on the following conjectures:
Conjecture G. The function 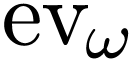 is a well-defined
is a well-defined 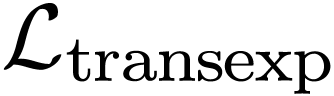 -embedding.
-embedding.
We defined [4] a derivation and composition law on 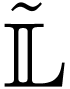 . we also expect that:
. we also expect that:
Conjecture H. The function 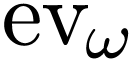 commutes with the derivation and composition laws on
commutes with the derivation and composition laws on 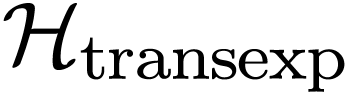 and
and 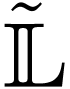 .
.
4.2Nested germs
A unique feature of surreal numbers is that they naturally contain
nested numbers, e.g. numbers whose expansion as a hyperseries is
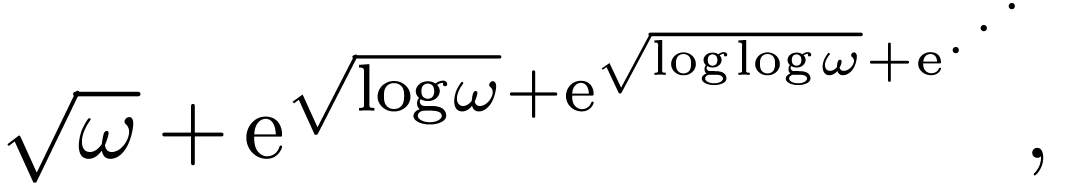 |
(4.2) |
where 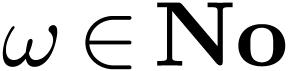 is a surreal number that plays the role of
a variable at infinity.
is a surreal number that plays the role of
a variable at infinity.
On the analytic side, the functional equation
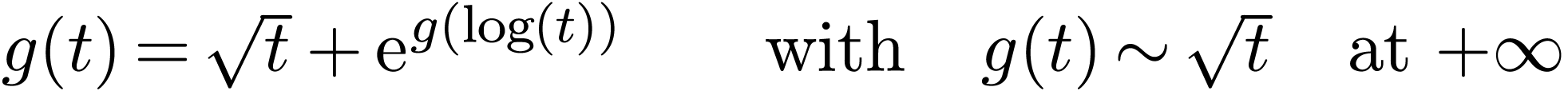 |
(4.3) |
naturally generates germs which, when represented using
logarithmico-exponential terms, expand in a similar way as (4.2).
There are good reasons [3] to believe that the behavior of
differential polynomials on these nested germs is the same as their
behavior on the corresponding nested numbers/hyperseries. Exploiting
this, I want to study how the functional equation (4.3) can
be solved in Hardy fields:
Question I. What linear orderings can be represented by
quasi-analytic sets of solutions of (4.3) lying in a common
Hardy field?
Bibliography
-
[1]
-
M. Aschenbrenner, L. van den Dries, and J. van der
Hoeven. Asymptotic Differential Algebra and Model Theory of
Transseries. Number 195 in Annals of Mathematics studies.
Princeton University Press, 2017.
-
[2]
-
M. Aschenbrenner, L. van den Dries, and J. van der
Hoeven. The surreal numbers as a universal H-field. Journal
of the European Mathematical Society, 21(4), 2019.
-
[3]
-
M. Aschenbrenner, L. van den Dries, and J. van der
Hoeven. Filling gaps in Hardy fields. https://arxiv.org/abs/2308.02446, 2022.
-
[4]
-
V. Bagayoko. Hyperexponentially closed fields. https://www.hal.inserm.fr/X-LIX/hal-03686767v1,
2022.
-
[5]
-
V. Bagayoko. Hyperseries and surreal numbers.
PhD thesis, UMons, École Polytechnique, 2022. https://theses.hal.science/tel-04105359.
-
[6]
-
V. Bagayoko. Equations over valued groups. https://arxiv.org/abs/2409.14854,
2024.
-
[7]
-
V. Bagayoko. Formal conjugacy and asymptotic
differential algebra. https://arxiv.org/abs/2409.17036,
2024.
-
[8]
-
V. Bagayoko. Groups with infinite linearly ordered
products. https://arxiv.org/abs/2403.07368,
2024.
-
[9]
-
V. Bagayoko. Hyperseries subfields of surreal
numbers. https://arxiv.org/abs/2409.16251,
2024.
-
[10]
-
V. Bagayoko. On ordered groups of regular growth
rates. https://arxiv.org/abs/2402.00549,
2024.
-
[11]
-
V. Bagayoko and J. van der Hoeven. The hyperserial
field of surreal numbers. https://hal.science/hal-03232836,
2021.
-
[12]
-
V. Bagayoko and J. van der Hoeven. Surreal numbers as
hyperseries. https://hal.science/hal-03681007,
2022.
-
[13]
-
V. Bagayoko, J. van der Hoeven, and E. Kaplan.
Hyperserial fields. https://hal.science/hal-03196388,
2021.
-
[14]
-
V. Bagayoko, L. S. Krapp, S. Kuhlmann, D. C.
Panazzolo, and M. Serra. Automorphisms and derivations on
algebras endowed with formal infinite sums. https://arxiv.org/abs/2403.05827,
2024.
-
[15]
-
M. Boshernitzan. An extension of Hardy's class L of
“orders of infinity”. Journal d'Analyse
Mathématique, 39:235–255, 1981.
-
[16]
-
J. H. Conway. On numbers and games. Academic
Press, 1976.
-
[17]
-
B. Dahn and P. Göring. Notes on
exponential-logarithmic terms. Fundamenta Mathematicae,
127(1):45–50, 1987.
-
[18]
-
J. Écalle. Compensation of small denominators
and ramified lineatisation of local objects.
Astérisque, 222:135–199, 194.
-
[19]
-
A. Fornasiero. Recursive definitions on surreal
numbers. ArXiv:math/0612234v1, 2018.
-
[20]
-
H. Gonshor. An Introduction to the Theory of
Surreal Numbers. Cambridge Univ. Press, 1986.
-
[21]
-
J. van der Hoeven. Operators on generalized power
series. Illinois Journal of Math, 45(4):1161–1190,
2001.
-
[22]
-
J. van der Hoeven. Transseries and real
differential algebra, volume 1888 of Lecture Notes in
Mathematics. Springer-Verlag, 2006.
-
[23]
-
I. Kaplansky. Maximal fields with valuations, ii.
Duke Mathematical Journal, 12(2):243–248, 06 1945.
-
[24]
-
H. Kneser. Reelle analytische Lösung der
Gleichung 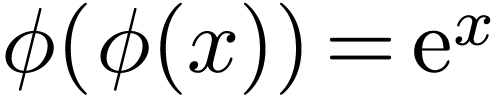 und erwandter
Funktionalgleichungen. Journal Für Die Reine Und
Angewandte Mathematik, 1950:56–67, 01 1950.
und erwandter
Funktionalgleichungen. Journal Für Die Reine Und
Angewandte Mathematik, 1950:56–67, 01 1950.
-
[25]
-
W. Krull. Allgemeine Bewertungstheorie. Journal
für die reine und angewandte Mathematik,
167:160–196, 1932.
-
[26]
-
S. Kuhlmann and M. Serra. The automorphism group of a
valued field of generalised formal power series. Journal of
Algebra, 605:339–376, 2022.
-
[27]
-
D. Marker and C. Miller. Levelled o-minimal
structures. Revista Matematica de la Universidad Complutense
de Madrid, 10, 1997.
-
[28]
-
A. G. Myasnikov and V. N. Remeslennikov. Groups with
exponents I. Fundamentals of the theory and tensor completions.
Siberian Mathematical Journal, 35(5):986–996, 1994.
-
[29]
-
A. G. Myasnikov and V. N. Remeslennikov. Exponential
groups II. Extensions of centralisers and tensor completions of
CSA groups. International Journal of Algebra and
Computation, 6(6):687–711, 1996.
-
[30]
-
A. Padgett. Sublogarithmic-transexponential
series. PhD thesis, Berkeley, 2022.
-
[31]
-
M. Saarimäki and P. Sorjonen. Valued groups.
Mathematica Scandinavica, 70(2):265–280, 1992.
-
[32]
-
J.-P. Serre. Lie Algebras and Lie Groups.
Springer-Verlag, 2nd edition, 2006.
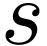 in a variable
in a variable 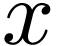 , that are
endowed with a hyperserial structure [13]:
a collection of functions
, that are
endowed with a hyperserial structure [13]:
a collection of functions 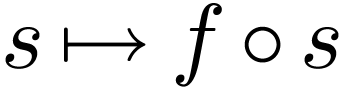 that are regular (e.g.
analytic and monotone) in a formal sense, and which are themselves
represented as hyperseries
that are regular (e.g.
analytic and monotone) in a formal sense, and which are themselves
represented as hyperseries 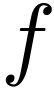 .
These functions include:
.
These functions include:
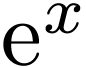 and logarithms
and logarithms 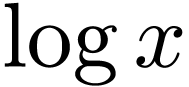 ,
,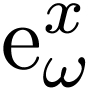 which satisfies Abel's equation
which satisfies Abel's equation
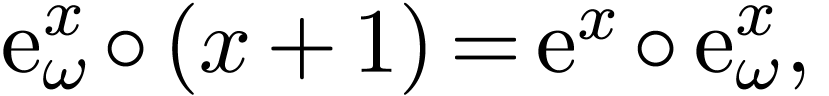
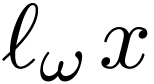 with
with 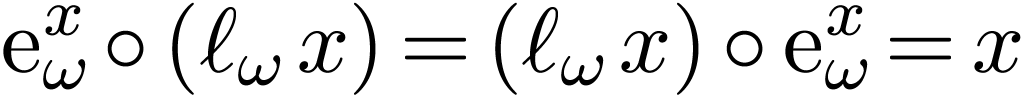 ,
,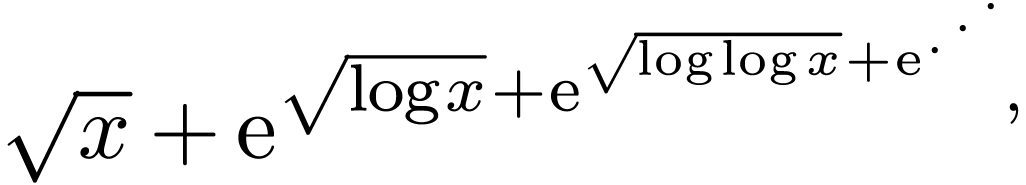
 of
surreal numbers has a natural hyperserial structure. This has sprouted a
series of research questions that are summarized below.
of
surreal numbers has a natural hyperserial structure. This has sprouted a
series of research questions that are summarized below.
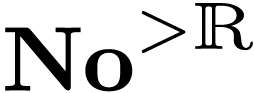 of positive infinite numbers, and to
differentiate them as such. In other words, this gives a
canonical way to define a composition law
of positive infinite numbers, and to
differentiate them as such. In other words, this gives a
canonical way to define a composition law 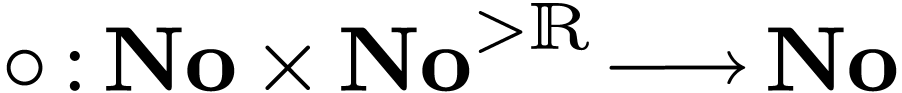 and a
derivation
and a
derivation 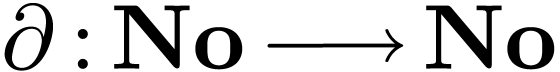 on surreal numbers. This is van der
Hoeven's conjecture:
on surreal numbers. This is van der
Hoeven's conjecture:
 that
are compatible with its hyperserial structure.
that
are compatible with its hyperserial structure.
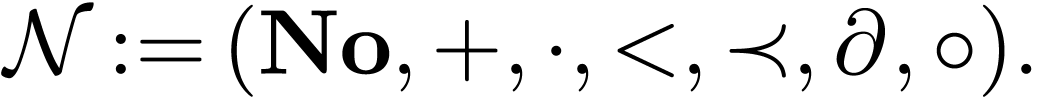
 and other such
structures.
and other such
structures.
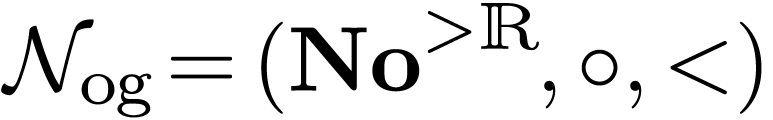 .
.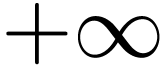 of definable unary functions in o-minimal expansions of
real-closed fields. Drawing on this connection, I introduced [
of definable unary functions in o-minimal expansions of
real-closed fields. Drawing on this connection, I introduced [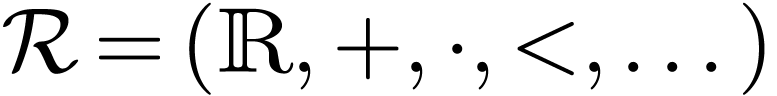 be an
o-minimal expansion of the real ordered field. The ordered group, under
composition and comparison at infinity, of germs at
be an
o-minimal expansion of the real ordered field. The ordered group, under
composition and comparison at infinity, of germs at 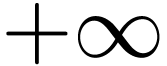 of unary
of unary 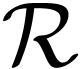 -definable
-definable is a growth order group.
is a growth order group.
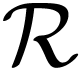 is levelled in the sense
of [
is levelled in the sense
of [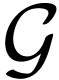 and a unary term
and a unary term 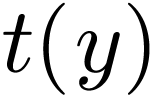 in the language of groups with parameters in
in the language of groups with parameters in  extending
extending 
 translates to an intricate functional equation
translates to an intricate functional equation
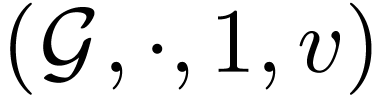 be a spherically complete,
torsion-free, nearly Abelian c-valued group. Suppose that its (Abelian)
residue groups are divisible. Then any equation
be a spherically complete,
torsion-free, nearly Abelian c-valued group. Suppose that its (Abelian)
residue groups are divisible. Then any equation
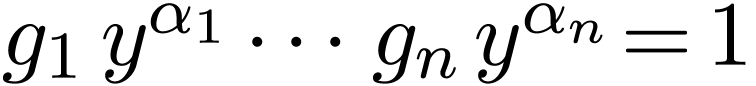
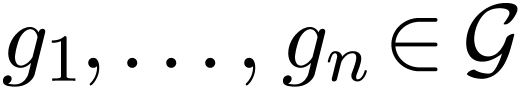 and
and 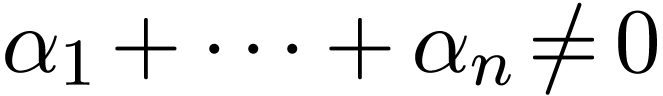 has a
unique solution
has a
unique solution 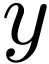 in
in 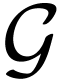 .
. where each
where each 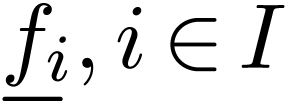 is a function
symbol, and an
is a function
symbol, and an 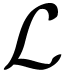 -theory
-theory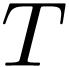 of dense linear orders without endpoints, whn and how
(and in what order) can one recursively define interpretations of the
function symbols
of dense linear orders without endpoints, whn and how
(and in what order) can one recursively define interpretations of the
function symbols 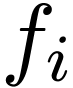 on Cartesian powers of
on Cartesian powers of 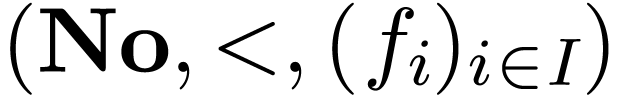 be a model of
be a model of 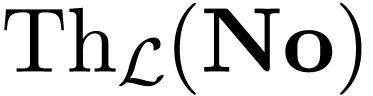 of
of  of strict dominance, and a notion of
infinite sums, for which linear maps commuting with infinite sums are
said strongly linear. They include for instance algebras of
formal power series in commuting or non-commuting variables, and Hahn
series fields and skew-fields. We showed:
of strict dominance, and a notion of
infinite sums, for which linear maps commuting with infinite sums are
said strongly linear. They include for instance algebras of
formal power series in commuting or non-commuting variables, and Hahn
series fields and skew-fields. We showed:
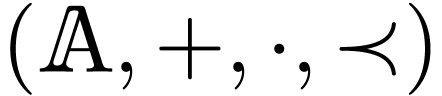 be an algebra, in characteristic
be an algebra, in characteristic  ,
,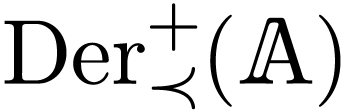 of strongly linear derivations
of strongly linear derivations 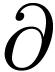 on
on  with
with 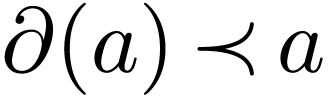 for all
for all 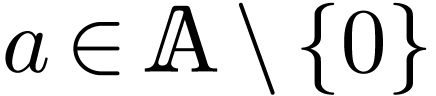 and the group
and the group 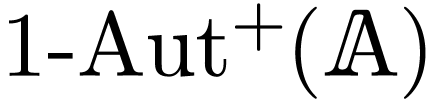 under
composition of strongly linear automorphisms
under
composition of strongly linear automorphisms  of
of
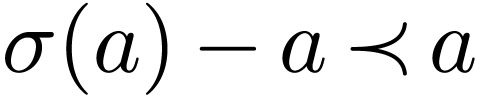 for all
for all 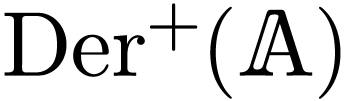 of
strongly linear derivations on
of
strongly linear derivations on 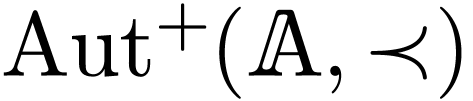 of strongly linear automorphism of
of strongly linear automorphism of 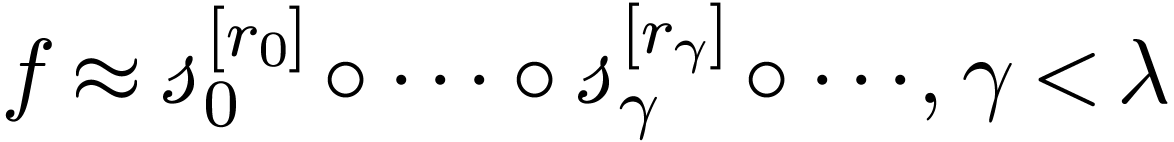
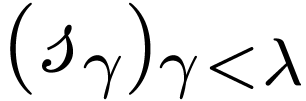 is a scale of functions that is strictly
decreasing in rate of growth,
is a scale of functions that is strictly
decreasing in rate of growth, 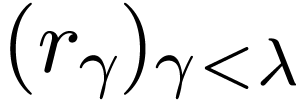 is a sequence of
non-zero real numbers, and
is a sequence of
non-zero real numbers, and 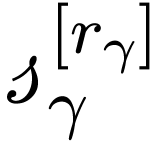 denotes the
denotes the 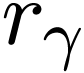 -th
-th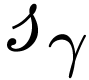 .
.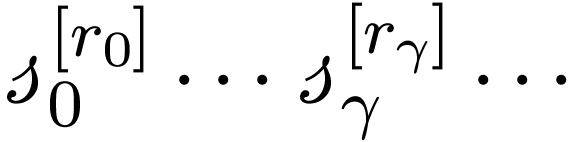 whose group operation depends only on the
assignment
whose group operation depends only on the
assignment 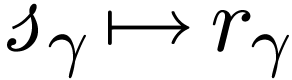 :
: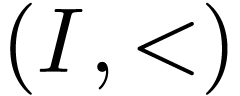 and a family
and a family 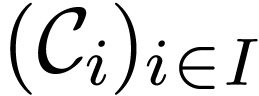 of Abelian ordered
groups, under what conditions can one define a group law
of Abelian ordered
groups, under what conditions can one define a group law  on the set
on the set 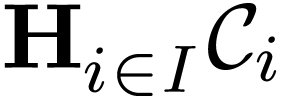 of functions
of functions 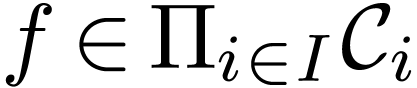 with anti-well-ordered support
with anti-well-ordered support 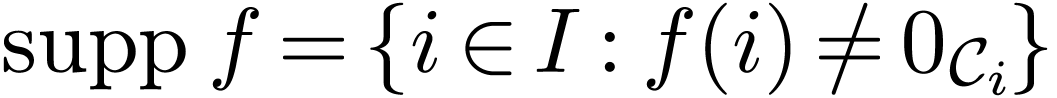 ,
,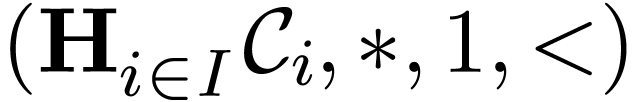 is a growth order group?
is a growth order group?
 be an ordered field, and let
be an ordered field, and let 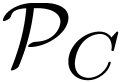 be the group under
composition of power series
be the group under
composition of power series 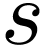 with
anti-well-ordered support, with exponents and coefficients in
with
anti-well-ordered support, with exponents and coefficients in 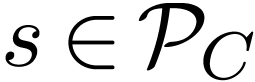 ,
,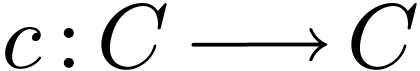 with anti-well-ordered support with
with anti-well-ordered support with 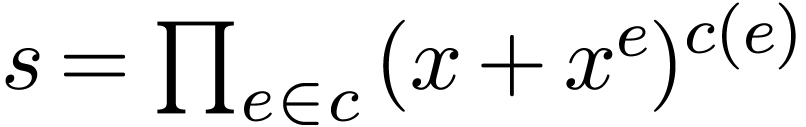 .
.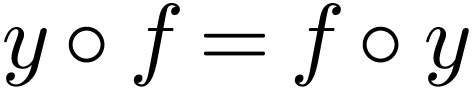 lie in a discrete Abelian subgroup, sometimes isomorphic to the group of integers, rational numbers or real numbers).
lie in a discrete Abelian subgroup, sometimes isomorphic to the group of integers, rational numbers or real numbers).
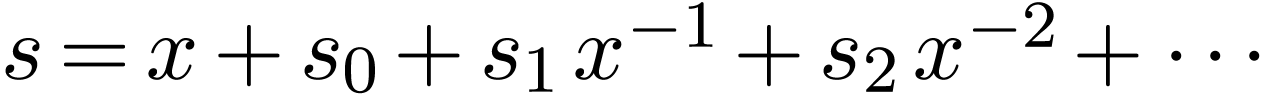 in
in 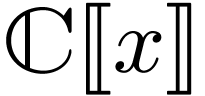 ,
,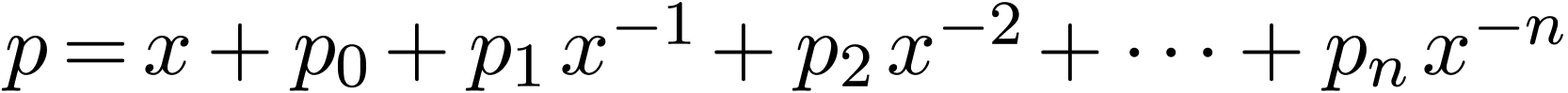 which is a conjugate
of
which is a conjugate
of 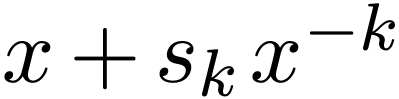 of
of 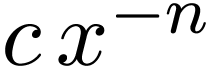 which depends on a longer truncation of
which depends on a longer truncation of  and derivation
and derivation 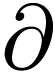 are defined on
are defined on 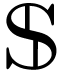 be a
direct limit of spherically complete differential subfields of
be a
direct limit of spherically complete differential subfields of 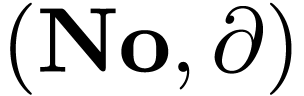 ,
, of parabolic elements in
of parabolic elements in 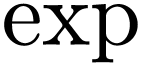 .
.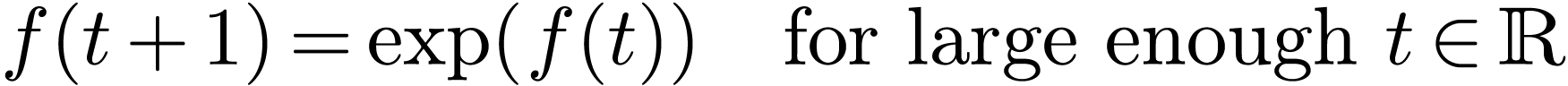
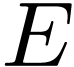 to
(
to
( is a natural candidate for
these o-minimal investigations. On the formal-surreal side, I hope that
the calculus of hyperseries on
is a natural candidate for
these o-minimal investigations. On the formal-surreal side, I hope that
the calculus of hyperseries on 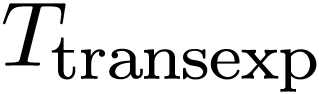 for
for 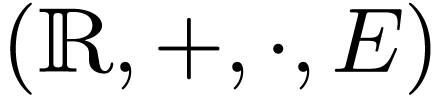 ,
,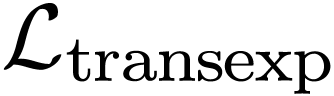 ,
,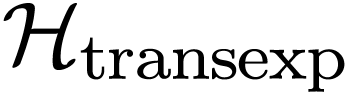 of germs of unary terms in
of germs of unary terms in 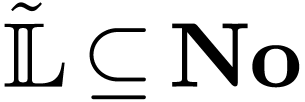 of finitely nested hyperseries [
of finitely nested hyperseries [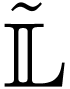 and the geometric/analytic model
and the geometric/analytic model 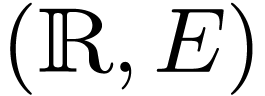 is to prove that there is a natural inclusion
is to prove that there is a natural inclusion
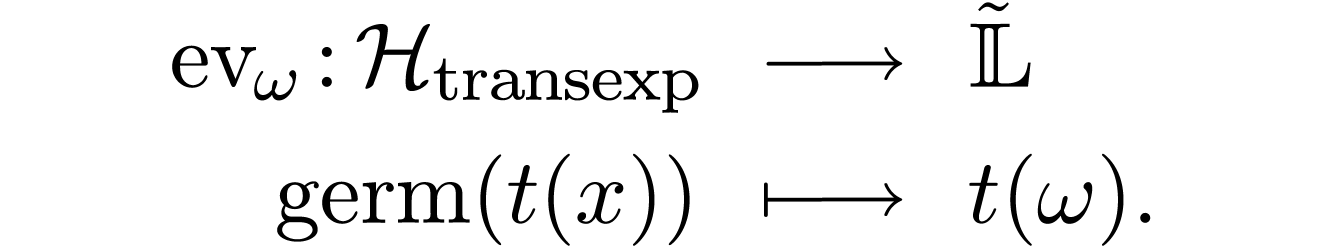
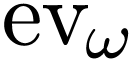 is a well-defined
is a well-defined 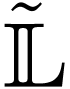 .
.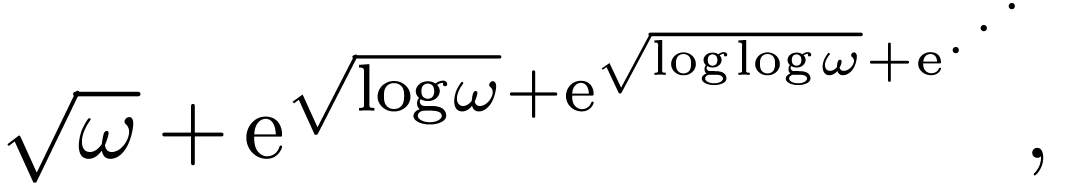
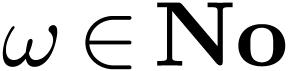 is a surreal number that plays the role of
a variable at infinity.
is a surreal number that plays the role of
a variable at infinity.
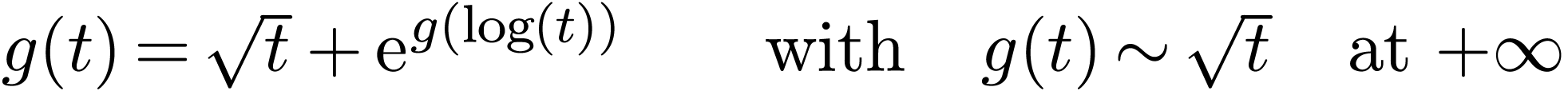
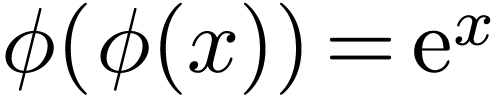 und erwandter
Funktionalgleichungen. Journal Für Die Reine Und
Angewandte Mathematik, 1950:56–67, 01 1950.
und erwandter
Funktionalgleichungen. Journal Für Die Reine Und
Angewandte Mathematik, 1950:56–67, 01 1950.